はじめての圏論 その第4歩：部分圏

「第4歩」と書いたからと言って続くかどうかはわからない -- というセリフはもうやめよう。はじめの何歩かは進んだから、もう、いつ中断してもいいからな。

で、第4歩のネタなんですが、もっともっと実例を出すか、一般的な議論をするか悩みました（少しだけ）。結局、今までの例から新しい例を作り出してみることにしました。与えられた圏から新しい圏を作り出す手続きを（圏論的）構成（construction）というのですが、構成は非常に重要です。例えば、純関数の圏から状態機械の圏を作り出すCirc構成、モナドを使って射の概念を拡張するKleisli構成*1、よい性質の射の対を選び出すEP（埋め込み／射影）構成、2つの圏C, Dから関手圏D^Cの構成、非決定性（の一種）を導入するベキ構成、トレース付きモノイド圏からコンパクト閉圏を作るInt構成（GoI構成とも呼ぶ）などが、新しい圏を大量生産する製造機械として活用されています。

今回紹介する部分圏は、構成と呼べるかどうかあやしいのだけど、与えられた圏の一部分を抜き出してそれを圏だとみなす方法です。

内容：

• 全体目次

部分圏の定義

C = (|C|, C, dom, cod, id, ;)が圏だとします。第2歩で述べたことだけど、圏の名前と射の集合に対して同じ‘C’を使っています（厳密には正しくない記法だけど、区別するのは面倒だから）。

D = (|D|, D, dom, cod, id, ;)がもうひとつの圏だとして、|D|⊆|C|、D⊆C（射の集合の包含関係）になっていて、Dのdom, cod, id, ;がCのdom, cod, id, ;をそのまま使ったもの（適用範囲は狭めるけどね）であるとき、DはCの部分圏だといいます。与えられた圏Cから部分圏を抜き出すには、対象の集合|C|の部分集合Xと射の集合Cの部分集合Yをうまく選んで、Cのdom, cod, id, ;がX、Yからはみ出さないようにすればいいのです。

第3歩で、どんな圏でも（空圏は例外）、モノイドを含むといいました。別な言い方をすると、どんな圏でもモノイドに相当する部分圏を含みます。例えば、行列の圏Matを考えて、({2}, Mat(2, 2), dom, cod, id, ;)を考えると、{2}⊆N、Mat(2, 2)⊆Mat であり、dom, cod, id, ; は、{2}とMat(2, 2)の範囲内でうまいこと働きます。つまり、2行2列の行列達は、あらゆる行列からなる圏Matの部分圏をなすわけね。

極端な部分圏達

しりとりの圏に固有名詞を付けてなかったので、以下、しりとりの圏をHShiri（Hiragana Shiritori; また劣情をもよおす人がいるかしら）という名で呼ぶことにしましょう。今までに導入した具体的な圏はHShiriとMatです。それと、極端な性質を持った圏の族として、離散圏、単一対象の圏、やせた圏も紹介しました。

離散圏、単一対象の圏、やせた圏は、典型的な圏ではなくて、辺境地帯の住人だといいました。しかし一方、どんな圏でも離散圏／単一対象圏を部分圏として（通常はたくさん）含んでいます。それを確認しておきましょう。

Hをひらがな文字の集合として、HStr1を長さ1のひらがな文字列の集合とすると、(H, HStr1, dom, cod, id, ;)は、しりとりの圏HShiriの部分圏であり、それ自身は離散圏となっています。また、すべての単位行列（対角成分が1、その他は0の行列）を集めた集合をUnitMatとします。UnitMat = {I₀, I₁, I₂, ...}（0行0列の単位行列も存在すると考えます）。すると、(N, UnitMat, dom, cod, id, ;)は、行列の圏Matの部分圏であり、離散圏ですね。

単一対象の圏（事実上モノイド）が部分圏として登場することは既に述べました。({し}, HShiri(し, し), dom, cod, id, ;)は、しりとりの圏HShiriに含まれる単一対象の部分圏です。HShiri(し, し)には、"しんぶんし", "しし", "しんし", "し", "しらいし"などが含まれますが、これらをしりとり結合してもHShiri(し, し)からはみ出すことはありませんから、ちゃんと圏になっているのです。

やせた部分圏

次は、行列圏Matからやせた部分圏（実際はとてもやせた圏）を抜き出しましょう。I_nはn行n列の単位行列を表しましたが、すこし一般化して、正方行列じゃなくても「対角成分が1で、その他が0」な行列を一般化単位行列と呼び、そのサイズを「列の数→行の数」の形で添えてI_n→mで表しましょう。

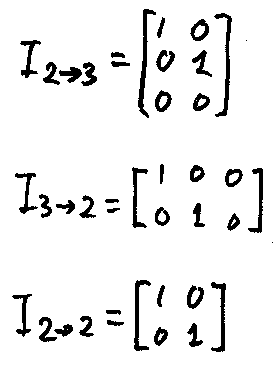
射として、n≦mである一般化単位行列I_n→mだけを採用するとやせた圏（実はとてもやせた圏）になります。この例はわざとらしい（人為的）ですが、この圏をUとして丁寧に書くと：

1. 対象の集合： |U| = N
2. 射の集合： U = {n≦m である I_n→mの全体}
3. 域： dom(I_n→m) = n
4. 余域： cod(I_n→m) = m
5. 恒等射： id_n = I_n→n = I_n
6. 結合： 行列の掛け算（図式順記法を使うなら逆順）

UがMatの部分圏になることは、行列の計算法則として I_m→k・I_n→m = I_n→m;I_m→k = I_n→k が成立することから確認できます。

この例がわざとらしいのは、自然数Nの普通の大小順序を無理やりに行列計算のなかに埋め込んでいるからですが、やせた部分圏を持つ状況は実は特殊です。なぜなら：

• 圏Cがやせた（とてもやせた）部分圏を持つ ⇔ 対象の集合|C|にプレ順序（順序）構造が入る。

つまり、Cからやせた部分圏を抜き出す作業は、|C|に（圏の構造と整合している）プレ順序構造を見いだす作業と同じです。

いくつかの射から生成された部分圏

圏Cの射をいくつか勝手に選んで、それらの射を含むような最小の部分圏を作ることができます。この構成法はかなり役にたちます。実例で示しましょう。

圏Matから、次の2つの射（行列ですね）を選びます。

1. 2行1列の行列（縦ベクトル）E1、[1 0]を縦にしたヤツ
2. 2行2列の行列S、1行目が[0 1]、2行目が[1 0]

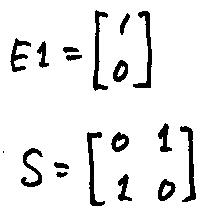
2つの射{E1, S}の範囲内なら、対象は{1, 2}だけで十分です。圏には恒等射が必須なので、対象1, 2に対して単位行列I₁, I₂は付け加えなくてはなりません。{E1, S, I₁, I₂}で結合（掛け算）が閉じているか、表を書いて調べてみます（1行目なら、E1;S = E2 と読む）：

＼	E1	S	I1	I2
E1	-	E2	-	E1
S	-	I2	-	S
I1	E1	-	I1	-
I2	-	S	-	I2

E1;S としてE2 = ([0 1]を縦にしたヤツ）が必要です。E2を加えれば：

＼	E1	E2	S	I1	I2
E1	-	-	E2	-	E1
E2	-	-	E1	-	E2
S	-	-	I2	-	S
I1	E1	E2	-	I1	-
I2	-	-	S	-	I2

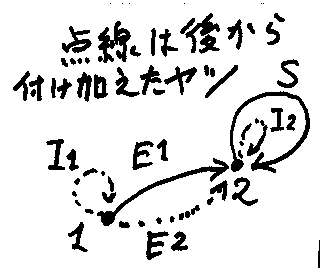
めでたく、2個の対象／5本の射を持つMatの部分圏が出来ました、とさ。

*1:Kleisliもカタカナ書きしたいのだけど、なんと読むのだろう？