このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

マスロフ式算数がやたらに面白いんですけど

雑記／備忘

インド式算数って、速算処方箋の寄せ集めでしょ。ロシア発のマスロフ式算数は、本質的に新しい演算を扱う奧が深い算数ですよ。マスロフ式算数を学んでも速算の役には立たないけど、背後にある数理的構造／現象の神秘に触れられるかもよ。

内容：

マスロフ式算数の由来

1980年代に、ロシアの物理学者マソロフ（Victor P. Maslov）により始められた脱量子化（Maslov Dequantization）という手法があり、現在では、数学、物理学、工学の広い範囲に影響を与えてます。マソロフ脱量子化の入り口は、変形した足し算を含む計算です。この計算は、普通の算数と同じ簡単な法則に従いますが、エキゾチックな世界を記述する道具になります。

このエキゾチックな算数の構造は、高校生なら十分に理解できるだろうし、指数計算の良い練習問題にもなると思います。というわけで、脱量子化された足し算を紹介します。

maxとminの算数

これから「数（すう、かず）」と言ったら、0より大きい実数の意味だとします。正の数だけで、ゼロも負の数も考えません。

2つの数a, bに対して、max(a, b)は「aとbの大きい方」だとします。正確に言うと、「小さくない方」です。a = b のとき、「大きい方」はありませんからね。同様に、max(a, b, c)は、「a, b, cのなかで一番大きい数」とします。これも、a = b や a = b = c のときを考えると、「一番大きい」は不適切ですが、細かいこと言わなくてもいいですよね。

maxに関して次が成立します。

  1. max(a, b) = max(b, a)
  2. max(max(a, b), c) = max(a, max(b, c))
  3. a×max(b, c) = max(a×b, a×c)

一番目は当たり前。2番目は、max(max(a, b), c) も max(a, max(b, c)) も、max(a, b, c) だからいいですね。3番目は、「aが正の数で、b≦c ならば、a×b≦a×c」が根拠になります。

max(a, b) を a∨b と二項演算記号で書いてみると、

  1. a∨b = b∨a
  2. (a∨b)∨c = a∨(b∨c)
  3. a×(b∨c) = (a×b)∨(a×c)

となるので、足し算に関する次の法則と同じ形になります。

  1. a + b = b + a （交換法則；可換律）
  2. (a + b) + c = a + (b + c) （結合法則；結合律）
  3. a×(b + c) = a×b + a×c （分配法則；分配律）

「aとbの小さい方」を min(a, b)、あるいは二項演算記号を使って a∧b と書くことにすると、やはり同じ法則が成立します。

  1. a∧b = b∧a
  2. (a∧b)∧c = a∧(b∧c)
  3. a×(b∧c) = (a×b)∧(a×c)

足し算的演算

maxを表す∨と、minを表す∧を二項演算と考えると、ほぼ足し算と同じように扱えます。正確に言えば、交換法則、結合法則、（掛け算に対する）分配法則が成り立っている、ということです。

なにか二項演算○があったとき、次の法則が成り立てば、○は「ほぼ足し算」と言っていいでしょう。

  1. a○b = b○a
  2. (a○b)○c = a○(b○c)
  3. a×(b○c) = (a×b)○(a×c)

∨と∧は「ほぼ足し算」あるいは「足し算的演算」の例でした。本物の足し算は当然に「足し算的演算」です。さて、他に「足し算的演算」はあるでしょうか？

この問題は、2変数の関数fで、次を満たすものを探す問題になります。

  1. f(a, b) = f(b, a)
  2. f(f(a, b), c) = f(a, f(b, c))
  3. a×f(b, c) = f(a×b, a×c)

興味がある人は、次を読む前に、そのようなfを探してみてください。

足し算的演算の実例

足し算的演算の例はけっこうあります。a×b をa*bと書き、スラッシュ「/」は割り算（分数）、sqrtは平方根だとして：

  1. sqrt(a2 + b2)
  2. a + b + 2*sqrt(a*b)
  3. a*b/(a + b)
  4. a*b/sqrt(a2 + b2)

などは足し算的演算になります。

興味がある人は、これらが実際に、交換法則、結合法則、（掛け算に対する）分配法則を満たすことを確認してみてください。

マスロフ和

前節の実例は、直観や努力で見つけたものではありません。実はズルしてます。足し算的演算をたくさん作りだす一般的な方法があるんです。

2つの数aとbに対して次の式を考えます。

  • (ak + bk)1/k

ここでkは定数です。kを決めるごとに、ひとつの足し算的演算が生み出されます。例えば、k = 2, k = 1/2, k = -1, k = -2 とすると、上の式は次のようになります。

  1. (a2 + b2)1/2
  2. (a1/2 + b1/2)2
  3. (a-1 + b-1)-1
  4. (a-2 + b-2)-1/2

これが、前節の4つの実例なのです（少し計算すれば、同一なのがわかります）。

(ak + bk)1/k を二項演算の形に書いてみましょう。

  • a [+]k b = (ak + bk)1/k

二項演算 [+]k をk-マスロフ和と呼びましょう*1。1-マスロフ和は普通の足し算； a [+]1 b = a + b です；2-マスロフ和は平方和の平方根；a [+]2 b = sqrt(a2 + b2) ですね。

k = 0 のときはk-マスロフ和が定義できません（1/0が定義できないので）。そうでなければ、kが負のときも含めて、任意のkに対してk-マスロフ和が定義できます。そして、kの値が何であっても次が成立します。

  1. a [+]k b = b [+]k a
  2. (a [+]k b) [+]k c = a [+]k (b [+]k c)
  3. a×(b [+]k c) = (a×b) [+]k (a×c)

このことを示すのに必要なのは、指数法則「xα×xβ = xα+β、 xα×yα = (x×y)α、(xα)β = xα×β」だけです。3番目の分配法則を示すときは、aを(ak)1/k に置き換えるのがミソです。

マスロフ和の極限

マスロフ和 [+]k のkを決めるごとにひとつの足し算的演算が決まります。その足し算的演算と掛け算で普通に算数ができます。つまり、kの値をいろいろ変えれば、それに応じてたくさんのマスロフ算数が手に入ります。

ところで、冒頭で挙げたmaxとminはマスロフ和では表現できません。maxとminの算数はマスロフ算数とは全然別物なのでしょうか？

実はなんと、max算数とmin算数は、マスロフ算数からの極限移行で得られるのです。マスロフ和 [+]k に含まれるkをどんどどん大きくしていくと、[+]kはmax演算に近づきます。これは、k→+∞の極限で、マスロフ和はmax演算になってしまう、ということです。象徴的に [+]+∞ = ∨ と書いてもいいかもしれません。

だいたいの雰囲気を説明してみます。a > b > 1 としましょう。aとbの差はごくわずかでもかまいません。kを大きくすると、akもakもどんどん大きくなります。が、akのほうがより速く大きくなり、bkとの差は開くばかりです。kが十分大きくなると、ak + bk ≒ ak となります。つまり、bk は無視してもよくなります。

わずかの格差でもそれが拡大し、小さい方の存在は無視されてしまう … イヤな世の中ですね。実際、kが大きいときのマスロフ和は、小さいほうを無視する“イヤな演算”になります。ak + bk ≒ ak なので、

  • (ak + bk)1/k ≒ (ak)1/k = a

つまり、

  • a [+]k b ≒ a

となり、[+]kは大きい方を選ぶ演算になります。

a > b > 1 という条件をはずしても、格差が拡大して小さい方が無視される現象に変わりはなく、k→+∞ではa, bがなんであっても、a [+]k b → max(a, b) となります。

いくつかの数 a1, a2, ..., an に対して、マスロフ和による総和 a1 [+]k a2 [+]k ... [+]k an は、k→+∞で、max(a1, a2, ..., an)に移行します。つまり、ナンバーワンしか生き残れない状況になります。あー、せち辛い。

k→-∞だと、事情が逆転します。象徴的に書けば [+]-∞ = ∧ 。[+]-∞では小さい方が支配的となり、大きい方が消え去ります。大小のスケールが逆転してますが、格差拡大のメカニズムは同じです。スケールの逆転（逆数を取る）に関しては次の公式が成立します。

  • (a [+]k b)-1 = a-1 [+]-k b-1

我々がいつも使っている足し算は、実は公平な足し算だったのですね。マスロフ和では、パラメータkにより不公平さを持ち込むことになります。k = +∞、k = -∞ では、究極的に不公平な足し算になります。それがmaxとminです。

プランク定数と脱量子化

k = 1/h と置けば、マスロフ和は次の形になります。

  • (a1/h + b1/h)h

kでもhでも本質的には同じですが、kの逆数であるhはプランク定数と呼ばれています。

プランク定数は物理で出てきますよね。僕は、物理のプランク定数が何であるか分からないのですが、マスロフは物理とのアナロジーで、マスロフ算数とその発展である脱量子化を構想したようです。

マソロフ脱量子化とその広大な応用分野を、要領よくまとめた報告である"MASLOV DEQUANTIZATION, IDEMPOTENT AND TROPICAL MATHEMATICS: A BRIEF INTRODUCTION"（http://glitvinov.googlepages.com/2007_JMS_426.pdf）に次の図が載っています。

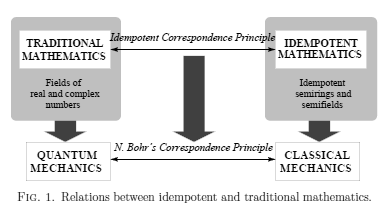
予断から勘違いしやすのですが、この図では、普通の算数や数学（左上のTRADITIONAL MATHEMATICS）が物理の量子力学に対応しています。普通の計算は、既に量子化されているのです。普通の計算を脱量子化（古典化）することにより、「量子力学：古典力学 ＝ 普通の計算：？」の疑問符のところを埋めよう、という魂胆です。

脱量子化するために、パラメータh（プランク定数；kの逆数）を導入し、hが0に近づく極限（古典極限）を見よう、というわけです。h = 1 での計算が量子的計算であり、h = 0 での計算が脱量子的計算となります。既に見たように、「量子的足し算＝普通の足し算＝公平な足し算」であり、「脱量子的足し算＝max演算＝格差が究極的に拡大する足し算」です。

いい忘れてましたが、脱量子化した計算では、マスロフ和の対数バージョンである a □t b = logt(ta + tb) を足し算に使い、普通の足し算を掛け算とするのが普通です。なにやらヤヤコシそうですが、対数パージョンのマスロフ算数は、今までに述べたマソロフ算数と、指数／対数で互いに移りあうように定義しているだけで、新しいものが出現したわけではありません。

上に挙げた"MASLOV DEQUANTIZATION, IDEMPOTENT AND TROPICAL MATHEMATICS: A BRIEF INTRODUCTION"には、ものすごく色んなことが書いてあって、僕は1%くらいしか理解できなかったんですが、その1%の20%くらいをこのエントリーに書いてみました。パラメータhが、量子現象と古典現象を結ぶらしいことは、行列計算を考えると割と分かりやすいので、気が向いたらそのことを書くかも知れません（気が向いたら）。

*1:この演算にこれといって呼び名がないようなので、僕が命名しました。