The n-Category Cafeというグループブログがあります。僕はたまに覗いてみるのですがサッパリ分かりません。まれに分かる部分があるとうれしいので、やっぱりたまに覗きます。
さて、The n-Category Cafe のn-categoryって何でしょう? nは任意の非負整数*1を表しているので、0-category, 1-category, 2-category, ... などを総称的にn-categoryと呼んでいます。higher dimensional category, higher category などとも呼ばれます。日本語だと、n-圏、高次元圏、高次圏などでしょうか*2。
一般的な定義は難しい(というか、現状、誰もわかってないようです)ので、2-圏の具体例をひとつ紹介して、n-圏の雰囲気をお伝えしましょう(それ以上の説明は僕には無理ですし)。この分野も用語法が混乱していますが、それに関する注意は最後に述べます。
内容:
| 1- 射 | 2-射 | |
| 横結合 | ; | * |
| 縦結合 | なし | ; |
最後の節では次の記法を提案してます。
| 1- 射 | 2-射 | |
| 横結合 | ; | ; |
| 縦結合 | なし | * |
しかし、後になって採用した記法は次です。「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」参照。
| 1- 射 | 2-射 | |
| 横結合 | * | * |
| 縦結合 | なし | ; |
有り体に言って「決まってりゃ、なんだっていい」のですが、他の記事を読む場合は注意してください。
また、この記事で使ってる「強/強い」という形容詞は、後で使うのをやめています。「高次圏: 用語法と文脈(主に2次元)」参照。
[/追記]
普通の圏は1-圏、集合は0-圏
圏は対象と射から出来ています。例えば、圏Cのなかの3つの対象と4本の射 f, f':A→B, g, g':B→C を絵に描くと次のようになります。
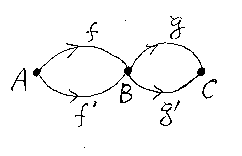
絵を見ると明らかなように、図形としての圏は、0次元の点と1次元の線(矢印)から構成されます。
では、1次元の線がなくて、0次元の点だけならどうでしょうか? それは点の集まりに過ぎません。つまり、単なる集合です。
以上の簡単な観察から、次のことがわかります。
- 0次元の点が、これといった構造なしに集まったモノが集合
- 0次元の点と1次元の線が、ある構造を持って集まったモノに、さらに結合(composition)という演算が備わると圏
そうであるなら、
- 0次元の点と1次元の線と2次元の面が、ある構造を持って集まったモノに、結合となんか別の演算も備わると、圏の2次元版ができるのではないか?
と、そういう期待が生まれます。この期待は現実となっていて、2次元版の圏やより高次元版の圏が存在します(その生態が解明されてませんが)。
圏の圏、2角形の演算、縦結合と横結合
圏の2次元版として最初に意識されたのは、おそらく圏の圏Catでしょう。2つの圏C、Dのあいだに関手F:C→Dがある状況は、2つの点とそれを結ぶ矢印で図示できるので、普通の意味の圏を構成します。圏Catの対象は圏で、その射は関手です。
さて、2つの関手F, G:C→Dのあいだには自然変換を考えることができます。α::F⇒G (コロンを2つと太い矢印を使う)が自然変換なら、それを次のように図示します。
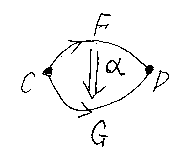
この図のαを、2角形の面だと考えます。2辺形や2角形は小学校で習わなかったかもしれませんが、辺が曲線でもいいなら辺と角が2つの図形を考えられます。詳細はともかく、2角形の演算として次の2種類を考えます。
- 辺を境界として隣り合っている2つの面(=2角形)をつなげて1つの面(=2角形)にする。
- 点を境界として隣り合っている2つの面(=2角形)をつなげて1つの面(=2角形)にする。
以下の図で、αとβは辺を境界として隣り合っていて、αとγは点を境界として隣り合っています。
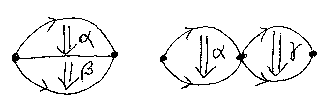
圏の圏とか自然変換とかが、なんかピンとこなくてもかまいません。それよりは、2角形の演算としての図形的イメージを持つほうが重要だと思います。今まで描いた図は標準的な図式法で、この図からのイメージにちなんで、αとβをつなぐことを縦結合(vertical composition)、αとγをつなぐことを横結合(horizontal composition)と呼びます(垂直結合、水平結合という言葉も使われます)。
例:順序集合の圏
圏の圏は、すこし面倒なので、その簡略版として順序集合の圏が2次元の構造を持つことを見てみましょう。
圏Cの対象は順序集合だとします。A∈|C|の順序を≦Aのように記しますが、混乱の心配がなければ単に≦と書きます。圏Cの射は単調写像です。ここで、写像f:A→Bが単調だとは、x ≦A y ならば f(x) ≦ B f(y) となることです。
ところで、圏Cの大きさなんですが、「すべての順序集合」を対象に含めると随分巨大です。「すべての有限順序集合」だと安心感があります。個々の有限順序集合は、ハッセ図として紙の上に完全に描けますから。なんなら、{0 < 1 < ... < n} という形の全順序集合〈線形順序集合〉だけを対象と考えて、それらのあいだの単調写像を射とする圏*3を念頭においてもいいです -- この圏は小さいので、圏全体を思い浮かべることができるでしょう。
圏Cの射 f, g:A→B に対して f ≦ g とは、「すべてのxに対して f(x) ≦ g(x)」と定義します。すると、ホムセットC(A, B) = HomC(A, B) が今定義した≦で順序集合になりますね。順序集合はやせた圏なので、C(A, B)は圏になっています。もっとはっきりと言えば、f, g∈C(A, B) が f ≦ g のとき、かつそのときに限り射[f, g]があると考えます。域・余域、恒等射、結合は次のとおりです。
- dom([f, g]) = f, cod([f, g]) = g
- idf = [f, f]
- [f, g];[g, h] = [f, h]
ここまでの話で、次のことが分かりました。
- Cは圏である。
- 圏Cの各ホムセットC(A, B)は圏である(特にやせた圏となる)。
全体としての圏のなかに、小さな圏がイッパイ詰まっているような構造になっています。宇宙のなかに小宇宙(銀河)がイッパイあるような感じでしょうか。小さな圏*4であるホムセットC(A, B)をホム圏(hom-category)と呼びます。
順序集合の圏は2次元の圏になっている
圏Cの対象はA, Bなど、射はf, gなどで表しました。f, g∈C(A, B)の順序関係 f ≦ g に対応する射[f, g]を一般的に表すときは、ギリシャ文字/コロン2つ/太い矢印を用いて α::f⇒g と書くことにします。fとgがA→Bであることを添えて、α::f⇒g:A→B と書くとより明確です。また、ホム圏C(A, B)におけるfの恒等射[f, f]はιf:f⇒f:A→B と書くことにします。ιはギリシャ文字イオタです。
次の事実は、ホム圏の定義から明らかでしょう。
- [結合律] α::f⇒g:A→B, β::f⇒h:A→B, γ::h⇒k:A→B に対して (α;β);γ = α;(β;γ)。
- [単位律] α::f⇒g:A→B に対して、ιf;α = α;ιg = α。
これらの等式(結合律と単位律)が成立してないなら、そもそも圏と呼べませんからね。
これまでに登場したモノどもをまとめておきます。
| 圏Cの構成要素 | 図形としてみると |
|---|---|
| 圏の対象A, B | 0次元の点 |
| 圏の射f, g:A→B | 点を結ぶ1次元の線(矢印) |
| ホム圏の射α::f⇒g | 線を結ぶ2次元の面(2角形、太い矢印) |
同じ記号「;」(セミコロン)を使ってますが、f;g は線の結合、α;β は面の結合なのです。線(矢印)の場合、つなぐための境界は点となりますが、面(2角形)の場合につなぐ境界は線または点となり、実際、境界線でつなぐ縦結合と境界点でつなぐ横結合があります。面=2角形=太い矢印の横結合はまだ述べてませんでした。
α::f⇒g:A→B、β::h⇒k:B→C の横結合 α*β::f;h⇒g;k:A→C は次のように定義される。
- α = [f, g], β = [h, k] として、α*β= [f;h, g;k]
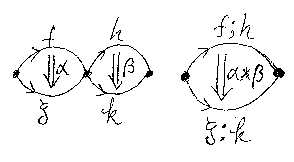
この定義が可能であることは、次の事実により保証されます。
- f ≦ g :A→B、h ≦ k :B→C のとき、f;h ≦ g;k : A→C
横結合に関しても、結合律と単位律が成立します。以下のεAは、対象Aの恒等射idAに対するホム圏の恒等射[idA, idA]のことです。
- [結合律] α::f⇒g:A→B、β::h⇒k:B→C、γ::u⇒v:C→D に対して、(α*β)*γ = α*(β*γ)。
- [単位律] α::f⇒g:A→B に対して、εA*α = α*εB = α。
さらに次の等式も成立します。
- f:A→B, g:B→C に対して、ιf*ιg = ιf;g
- α::f⇒g:A→B, β::g⇒h:A→B, γ::u⇒v:B→C、δ::v⇒w:B→Cに対して、(α;β)*(γ;δ) = (α*γ);(β*γ)。(下の図も参照)
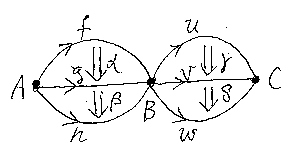
二番目の等式を(場合により一番目の等式も含めて)交替律(interchange law)と呼びます。
これらの法則は、αやらβやらが、順序から導かれる射であることに戻って確認できます。今までに登場した演算は次のとおりです。
| 圏Cの構成要素 | 演算 |
|---|---|
| 圏の対象A, B | なし |
| 圏の射f:A→B, g:B→C | 結合 f;g:A→C |
| ホム圏の射α, β∈C(A, B) | 縦結合 α;β∈C(A, B) |
| ホム圏の射α∈C(A, B), γ∈C(B, C) | 横結合 α*γ∈C(A, C) |
1次元の演算を1つと2次元の演算を2つ備えた2次元的な構造物、これが2次元の圏なのです。
高次圏に関連する概念/記法/用語
この記事では、縦結合を「;」、横結合を「*」で表しました。縦結合は普通の結合に近い感じ(?)がするし、横結合はスター積なんて呼ぶ人もいるので、こうしたのですが、むしろ横結合に「;」を使ったほうが整合性はあるようです。横結合に「;」を使うと、ιf*ιg = ιf;g が次の形に書けます。
- ιf;ιg = ιf;g
縦結合に黒丸、横結合に白丸(あるいはその逆)なんて記号を使う人もいます。横結合にテンソル積の記号を使う例もありました。まー、とにかく色々。
例として出した順序集合の圏は2次元の圏ですが、豊饒圏の概念を使うと、圏の圏Catに直積を考えた対称モノイド圏で豊饒化された圏になります。横結合*が、C(A, B)×C(B, C)→C(A, C) という関手になっています。*は直積圏からの関手なので双関手ってことになります。双関手条件を述べたのが交替律です。
では、2次元の圏はCat-豊饒圏(Cat-enriched category)なのかというと、そうはいきません。多くの実例では、結合律と単位律が等号の意味では成立してなくて、ホム圏の同型だけの差を無視した(up-to-isoな)結合律と単位律しか成立しません。法則がup-to-isoでしか成立しないようなn-圏は弱いn-圏(weak n-category)、等式として法則が成立しているなら、強いn-圏(strong n-category)と呼びます。「弱い」の代わりに「緩い」(relaxed)、「強い」の代わりに「厳密」(strict)を使うこともあります。
歴史的な事情から、弱い2-圏、弱い3-圏は別な呼び方があり、単に2-圏、3-圏と言うと、強いn-圏の意味になります。
| 次元 | 強いn-圏 | 弱いn-圏 |
|---|---|---|
| 2 | 2-圏 | 双圏(bicategory) |
| 3 | 3-圏 | トライ圏(tricategory) |
| 4 | 強4-圏、厳密4-圏 | 弱4-圏、緩4-圏、テトラ圏(tetracategory) |
| n > 4 | 強n-圏、厳密n-圏 | 弱n-圏、緩n-圏 |
日本語だと、tri, tetraの訳語がないのも困りものです。(bicategory=二圏、tricategory=三圏 などはどうかとも思いましたが、2-圏、3-圏と口頭で区別がつかない ^^;)
強いn-圏はほぼ合意された定義がありますが、弱いn-圏の定義は山ほどあり、それらが同値であるか、そうでないかの確認はできてないようです。
2-圏(強い2-圏)、双圏(弱い2-圏)とは別に、二重圏(double category)という概念もあります。一言でいえば、圏の圏Catのなかの内部圏(圏対象)のことです。定義も扱い方も2-圏/双圏とは違うのですが、高次圏論の文脈では「2次元の圏の異なった側面」という程度の違いしかない(大枠では統合される)ような気がします。
オマケ
http://math.ucr.edu/home/baez/trimble/tetracategories.html から参照されているPDFに、テトラ圏(弱4-圏)の諸法則を書き下した手書き原稿があります。もう、凄まじいですね。n = 5 になると、もう人間が作業するのは無理そう。計算機の出番でしょう。