このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

この機会にマスターしようぜ、正規表現、構文図、オートマトン

雑記／備忘

正規表現と構文図について解説します。オートマトンについても詳しく述べます。オートマトン・スゴロクで遊びましょう！

世間でよく知られている／使われている概念・方法にはこだわらず、僕（檜山）の感覚で一番わかりやすいと思われる筋書きと用語法／図式法を使って説明します。この記事に目を通して“感じ”が掴めたら、形式言語理論の教科書を読み始めることが出来るでしょう。

[追記]この記事の内容に対する具体例は、「正規表現とオートマトン：なんだ簡単じゃん、JavaScriptによる実装」にあります。[/追記]

内容：

関連するエントリー：

正規表現

まずは正規表現ですが、これについてはある程度ご存知であると仮定します。とはいえ、正規表現には色々な方言がありますから、この記事で使う記法を確認しておきます。

  1. カンマ「,」： 連接を表します。
  2. 縦棒「|」 ： 選択を表します。
  3. 疑問符「?」 ： 省略可能であることを表します。
  4. 星印「*」 ： 任意回（0回でもよい）の繰り返しを表します。

正規表現を組み立てるときの基本素材となる記号は、原子記号（atomic symbol）、終端記号（terminal symbol）、文字（letter）とか呼ばれます。ここでは基本記号という言葉を使います。（それに対して、先に触れたカンマや縦棒などは、構文的な演算子記号です*1。）基本記号は、a, b などの英小文字で表すことにします。英小文字は、実際の基本記号そのものを表すときと、基本記号を値とする変数として使うことがあります。が、定数と変数の区別をあまり神経質にする必要はありません。

使用するすべての基本記号からなる集合はアルファベットと呼ばれます。アルファベットは、英字の集合とは限らず、どんな集合でもかまいません。例えば、1から100までの整数の集合をアルファベットとしてもいいのです。ときに、無限集合をアルファベットにすることもあります。以下では、アルファベットをAで表します*2。

念のために、正規表現の定義をきちんと述べておきます。

  1. 基本記号は正規表現である。
  2. E, F が正規表現のとき、(E, F) は正規表現である。
  3. E, F が正規表現のとき、(E | F) は正規表現である。
  4. E が正規表現のとき、E? は正規表現である。
  5. E が正規表現のとき、E* は正規表現である。
  6. 以上に定義したものだけが正規表現である。

このような定義の方法を帰納的定義（inductive definition）といいます。帰納的定義を簡略に表すために正規表現が使われることがあります。次は「正規表現を帰納的に定義する正規表現」です。x は基本記号、E は正規表現を表します。

  • E ::= x | '(' E ',' E ')' | '(' E '|' E ')' | E '?' | E '*'

簡略すぎてかえって分かりにくいかもしれませんね。わかんなくても、別に気にしなくていいですよ。

正規表現の例

アルファベットAを、A = {a, b, c} として、いくつかの正規表現の事例を示します。

  1. a
  2. (a, b)
  3. c*
  4. ((a | b) | c)
  5. (a, ((a | b) | c)?, b*)
  6. ((a, ( b | c), b?)*, (a*, c))

((a, b), c) と (a, (b, c)) は同じとみなして (a, b, c) と書いてもいいことにします。((a | b) | c) と (a | (b | c)) も同様で、 どちらも (a | b | c) と書けます。

演算子の優先順位（結合の強度）を次のように定義しましょう。

  1. 優先順位が高い／結合の強度が強い 「?」と「*」
  2. 優先順位が中くらい／結合の強度が中くらい 「,」
  3. 優先順位が低い／結合の強度が弱い 「|」

この優先順位に基づき、丸括弧は適宜省略することにします。また、加減乗除で掛け算記号を省略するのと同様に、連接の演算子「,」を省略することもあります。

以上の省略ルールを適用すると、(a, ((a | b) | c)?, b*) は a(a|b|c)?b* と短く書けます。ただし、この記事内ではカンマは省略せずにちゃんと書きます。

構文図

構文の定義に構文図を使った事例としては、JSONが有名ですね。例えば、次は「JSONオブジェクト」の構文を定義する構文図です。（[追記]この図に関する注意として、コメント欄を参照のこと[/追記]）

Wikipediaの項目 http://en.wikipedia.org/wiki/Syntax_diagram にも構文図の例がいくつか載っています。

構文図（syntax diagram）は、ある種の有向グラフです。ノードと向きの付いた辺から構成されます。向きを示すのに普通は矢印を使いますが、ここでは電荷（charge）も併用します。電荷（極性（polarity）とか符号（sign）ともいいます）は、プラスとマイナスのことです。電荷と向きの関係は毎度悩むのですが、マイナスからプラスの向きと決めます。

マイナス記号が描かれたノードが始点、プラス記号が描かれたノードが終点になります。

では、正規表現の帰納的な定義に沿って、対応する構文図を定義していきましょう。以下に紹介する描き方は一番標準的というわけではありませんが、僕はこれが使いやすいと思っています*3。

基本記号

基本記号は次のように描きます。基本記号が描かれたノードを記号ノードと呼ぶことにします。記号ノード以外に、始点のマイナスノードと終点のプラスノードも描きます*4。

連接

一般に、なんらかの正規表現に対応する図を四角で描くことにします。E、F などの英大文字は、既に描かれている図に付けた呼び名です。連接 (E, F) を図示すると次のようになります。プラスノードとマイナスノードが接合されて黒丸のノードになることに注意してください。

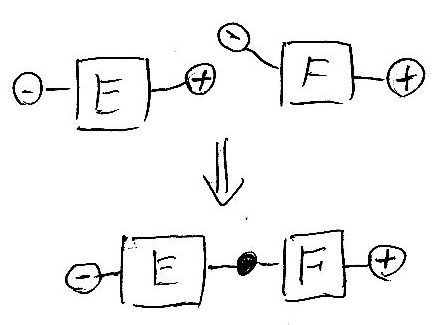
選択

次は選択です。マイナスノードどうし、プラスノードどうしを重ね合わせます。重なったノード達は、1つのマイナスノードと1つのプラスノードになります。

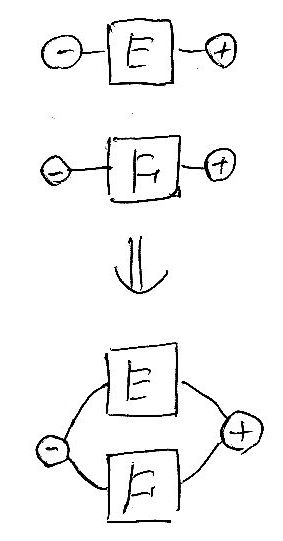
省略可能

省略可能性（オプショナル）を図示するには、マイナスノードからプラスノードに辺を一本加えます。加えた辺は、中間にノードを持たない単なるワイヤーです。

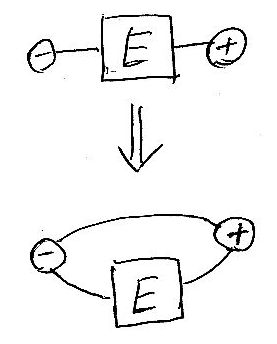
繰り返し

最後は繰り返しの図示ですね。ワイヤーを本体にグルリと巻きつけて、スタートのマイナスノードを通過させて前方に出す感じです*5。

[追記]この繰り返しの構成は、ノードの個数を節約し過ぎですね。繰り返しを作る目的は達成してますが、連接や選択の構成を一緒に使うときは具合が悪いかもしれません。開始点であるノードに入る辺があると、状態遷移の意図せぬ“逆流”や“混線”が起きます。あまりケチケチせずにノードを1個増やしたほうが無難です。[/追記]

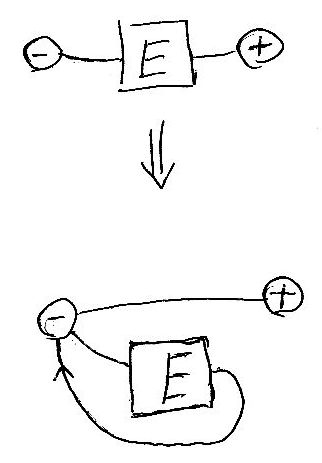
ストレートワイヤーによるレイアウト調整

今導入した方法で正規表現を図示すると、ノード数が少なくコンパクトな絵を描けます。しかし、レイアウト的には窮屈な印象になり、ワイヤーの引き回しがゴチャゴチャしがちです。例えば、正規表現 *6。εは、基本記号が出現しないこと、つまり空列を表すので、(ε, E) = (E, ε) = E となり、連接演算の単位元となります*7。εに対応するストレートワイヤーは次のようです。

εに対応するストレートワイヤーを付け足しても黒丸のノードが増えるだけで構文図のつながり具合は変更されません。構文図の両端だけではなくて、中間のワイヤーをちょん切ってストレートワイヤーを挟んでもかまいません。このとき黒丸ノードが2個増えます。黒丸ノードは、つながり具合（トポロジー）には影響しないので適当に増やしたり減らしてもかまいません。

有限状態オートマトン

正規表現から作った構文図は、そのままオートマトンとして使えます。

まず、構文図のマイナスノード、プラスノード、黒丸ノードに適当に番号をふります。それから、記号ノードを取り除き、同じ場所に同じ記号を“辺（ワイヤー）のラベル”として貼りつけます。この操作により、次のような「辺にラベルが付いた有向グラフ」ができます。ただし、もとのイプシロン辺にはラベルが付いてません。

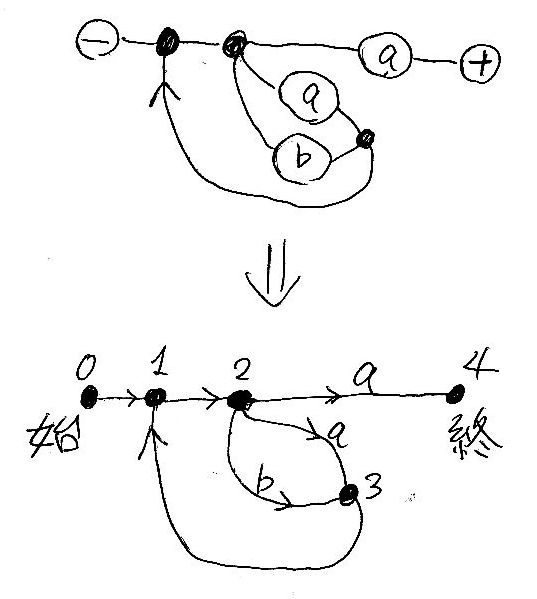
この有向グラフのノードが状態点です。有向辺が状態遷移（の経路）を表します。（実際の状態遷移手順はすぐ後で述べます。）もとのマイナスノードが始状態、もとのプラスノードが終状態という特別な状態として識別されます。

このようにして正規表現から作られた有限状態オートマトンはどのように動作するのでしょうか。次の節で述べます。

有限状態オートマトンの実行

オートマトンは、状態遷移マシンの一種です。実際のコンピュータやプロセスと同様に、逐次実行方式と並列実行方式がありますが、ここでは逐次実行（直列順次実行）を考えます。マシンの現状態（カレントステート）が常に1つ決まっています。入力があると、その入力にトリガーされて、状態が変化します。これが状態遷移です。「変化する」には状態が変わらない（同じ状態にとどまる）ことも含まれます。状態と状態遷移は、有向グラフのノードと辺により完全に記述されます。

正規表現に対応するオートマトンに入力可能なデータの集合は、最初に指定したアルファベットAです。例えば、A = {a, b, c}。入力終了を明示的に知らせるエンドマーカー記号をAに付け加えます。エンドマーカーは、習慣上ドルマーク「$」を使うことが多いようです。ファイル入力に例えるなら、「$」はEOF（End Of File）に対応する特殊記号です。以下では、入力の時系列を [a, b, a, c, $] のようなリストで表すことにします。

状態遷移マシンの実行開始時点（ほんとの機械なら電源投入時点）では、状態が始状態（前もって決まった初期状態）にセットされます。基本記号が1個入力されると、それによって次の状態点へ移動します。このとき、次のルールに従います。

  • 現状態点から、“入力された基本記号と同じラベルが付いた辺”が出ていれば、その辺をたどって次の状態点に移動してよい。
  • “入力された基本記号と同じラベルが付いた辺”が1本もないときは失敗（失敗の処理は後述）
  • 現状態点から、ラベルが付いていない辺（イプシロン辺）が出ていれば、入力と無関係に自由にたどってよい。

入力の列、例えば [a, b, a, a, $] がオートマトンによって受理（accept）されるとは次のことです。

  1. 始状態から、入力「a」による状態遷移が成功する。
  2. 現状態から、入力「b」による状態遷移が成功する。
  3. 現状態から、入力「a」による状態遷移が成功する。
  4. 現状態から、入力「a」による状態遷移が成功する。
  5. 現状態は終状態で、エンドマーカー記号「$」が入力された。

状態遷移が失敗したとき、その入力列は受理不可能なモノでしょうか？ そうとも言えないんですよね。多少の失敗があっても、人生を捨てちゃいけないよ、ってことです。詳しくは次節で。

バックトラックと先読み

状態遷移のルールを再掲します。

  • 現状態点から、“入力された基本記号と同じラベルが付いた辺”が出ていれば、その辺をたどって次の状態点に移動してよい。

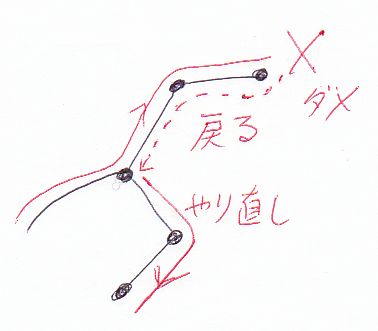
このルールが適用されるとき、“入力された基本記号と同じラベルが付いた辺”は一本とは限らないのです。ここで選択が生じるのです。ヘタな選択をすると、行き詰まって状態遷移が失敗します。しかし、選択を行った地点まで戻って別な選択肢を選ぶとウマクいくことがあります。

戻って別な選択肢を選んでやり直すことをバックトラックといいます。普通は、一番最後（直近）に選択をした場所まで戻ります。理論的には「同じ轍を踏まない」なら、どんな方法でバックトラックしてもかまいません。「同じ轍を踏まない」ためには、以前の選択や既に入力された記号列を保存しておく必要があります。これは、オートマトン実装の手間と実行効率の両方の意味で負担となります。

バックトラックをやり尽くしても、結局は失敗することもあります。そんなときは、その入力列を受理でないことになります。入力列は拒否（refuterefuse）されたとも言います。単に状態遷移が失敗したからといって、入力例を拒否することはできません。ありとあらゆる可能性をやり尽くしてみて、どうやってもダメだと分かって初めて拒否できるのです。

バックトラックと似た効果をあげる方法として先読みがあります。これは、選択を保留して様子見するのです。1個の入力記号で判断できない状況で、引き続く何個かの入力を眺めて決定を下します。バックトラックが「ダメモトでもとりあえずやってみる」態度なのに対し、先読みは「しばらく待ってから決定をする」態度ですね。先読みも、余分なメモリやメカニズムが必要なので、処理は複雑になります。

スゴロクとオートマトン

僕が説明するネタって、たいていは時間的に変動する絵を使うので、アニメーションを使うのが一番効果的な気がします。でも、アニメーション資料は作れないので、代わりにスゴロクを使った「オートマトン遊び」を紹介しますからやってみてください。

アルファベットが A = {a, b, c} なら、エンドマーカー記号を付け加えて {a, b, c, $} が入力記号の集合です。この場合は、四面体（三角錐）のサイコロを使い、各面に a, b, c, $ を書き込んでおきます。

紙に有向グラフを描きます。辺には、a, b, c のラベルを付けます。ラベルがない辺（イプシロン辺）を入れておいてもいいです。スタートノード（始状態）とゴールノード（終状態）を決めておいてくださいね。

さて、ゲーム開始です。スタートノードにコマを置いて、サイコロを振ります。出た目により移動先を決めます。バックトラックが許されるので、コマが移動した経路は色を塗るとか別紙に記録するとかして後から分かるようにしてください。ラベルがない辺に沿った移動はサイコロの目と無関係にいつでもできます。

出たサイコロの目と一致するラベルの辺がないときは失敗ですが、バックトラックが可能なら戻って別な経路を進むことができます。移動に失敗し、バックトラックの余地もなくなったら、あなたは失格。「サイコロの目の履歴＝入力の記号列」は拒否されます。コマがゴールノードにある状態で、サイコロ振って「$」が出れば成功です。おめでとうございます。「サイコロの目の履歴＝入力の記号列」は受理されます。

バカバカしい？ そんなこと言って手を動かさないといつまでたっても実感として理解できないと思いますよ。

コマをたくさん使うスゴロクと並列処理

しばらくオートマトン・スゴロクで遊んでいると、バックトラックによりイチイチやり直すのが面倒になります。もっといい方法がないでしょうか？ コマをたくさん使って、最初からすべての可能性を押さえておいてはどうでしょう。

例えば、サイコロを振って「a」が出て、「a」により進める道が2本あったとき、コマを1つ増やして2箇所にコマを置きます。同時に複数のコマを管理することになりますが、後戻りする面倒は避けられます。どれか1個のコマがゴールノードにあるときに「$」が出ればアガリです。逆に、「$」が出たとき、ゴールノードにいる自分のコマがないなら失格です。

1つのスゴロク盤の上を複数のコマが同時に動き回る状況は、並列処理の簡単な例になっています。それぞれが独立な状態を持つ複数のプロセッサに入力（サイコロの目）がコピーされるシステムですね。実行中にプロセッサの数が増えるので、状態空間の全体（プロセッサごとの状態空間の直積）もどんどん大きくなります -- 失敗した経路に対応するプロセッサは停止破棄していいから、アクティブなプロセッサが減ることもあるけど。

非決定性オートマトンと決定性オートマトン

バックトラック、先読み、並列処理などが必要になるのは、入力に対する状態遷移の行き先が一意的に決まらないからです。このような状態遷移の不定性を持ったオートマトンを非決定性オートマトン（nondeterministic automaton）と呼びます。一方、どの状態点（有向グラフのノード）においても、状態遷移が失敗するか、状態遷移先が1個だけに決まるとき、そのオートマトンを決定性オートマトン（deterministic automaton）と言います。

オートマトンをプログラムにより実装するときは、決定性オートマトンのほうが簡単だし高速で有利なんですが、理論上は非決定性オートマトンのほうが扱いやすいのです。この「決定性／非決定性のギャップ」で四苦八苦することになりますが、その話は今日はしません。

正規表現とオートマトン

正規表現Eから構文図を経由して有限状態オートマトンMを作りました。ある記号列が正規表現Eにマッチすることと、その記号列が有限状態オートマトンMに受理されることは同値です。有限状態オートマトンが先に与えられたとき、それと同等な正規表現を作ることもできます。より一般に、次のような方法で定義される言語（記号列の集合）は同じ種別のもので、正規言語（regular language）と呼ばれます。

  1. 右線形文法
  2. 左線形文法
  3. 拡張BNF記法
  4. 正規表現
  5. 有限状態オートマトン

他に、クリーネ（クリーニ）代数や圏論を使った定式化もあります。フラクタル幾何や離散力学系にも正規言語やその拡張である文脈自由言語が出現します。詳細は形式言語の教科書を眺めてください。

この記事では、暗黙にオートマトンのアルファベットと状態空間は有限だと仮定していますが、無限アルファベット／無限状態空間を考えることは重要です。現実のコンピュータのアルファベットや状態空間は有限ですが、あまりにも巨大な有限なので、無限で近似したほうが扱いやすくなります。よって、コンピュータとソフトウェアのモデルに無限オートマトンを使うことがあります。

他の文献を読むときの注意

「世間でよく知られている／使われている概念・方法にはこだわらず」の方針でこの記事を書いたので、最後に一般的な概念・方法との違いを注意しておきます。

構文図の端点に電荷を与えることは、ほとんど前例がないかも知れません。電荷と電流（電子の流れ）を考えると、2つの構文図を連接で繋ぐとき、回路の直列結合との類似が成立します。選択は回路の並列結合ですね。構文図を圏論的に考えるときは、コンパクト閉圏を使うのが一番ふさわしいと思うのですが、そのとき、電荷や電流を本質的に利用します。

正規表現から構文図を経由して作ったオートマトンは、始状態点も終状態点も1個ですが、一般にはオートマトンの終状態点はたくさんあってもいいのです。正規表現からオートマトンを作る方法は、マクノートン・山田*8（McNaughton-Yamada）、グラシュコフ（Glushkov）などの構成法が古くから知られています。それらの構成法では、終状態点が複数個現れることがあります。

この記事では、エンドマーカー記号「$」を導入して、「終状態点にいるときに$を入力したら受理」と定義しました。普通は、エンドマーカー記号は導入せずに、「最後の入力により終状態点に遷移したら受理」と定義します。ほとんど差はないのですが、明示的なエンドマーカーがあったほうが僕は分かりやすく感じます*9。

[追記]この記事の内容に対する具体例は、「正規表現とオートマトン：なんだ簡単じゃん、JavaScriptによる実装」にあります。[/追記]

*1:構文的な演算子記号を、メタ記号、メタ文字と呼ぶこともあります。

*2:アルファベットはΣで表すことが多いのですが、ここでは英字を使います。

*3:実は、圏論との相性が非常に良いのです。トレース付きモノイド圏、コンパクト閉圏による定式化まで、この描き方をそのまま使い続けることができます。

*4:基本記号にマイナス記号やプラス記号が入っていたときに困りますね。ウーン、色塗るとかノードの形を変えるとかして対処してくださいな。

*5:省略可能は縄跳びで、繰り返しはゴルフと覚えたらいいかも。

*6:a|b)*, a) はこうなります。 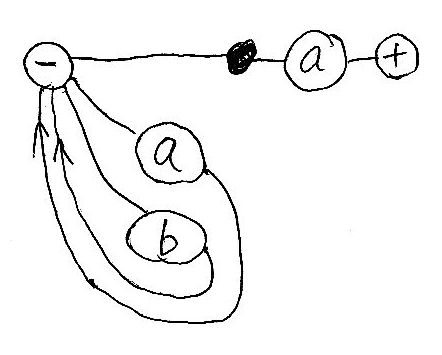もう少し余裕を持ったレイアウトにしたほうが見やすいですね、例えば次のように。（[追記]アリッ、矢印が一箇所間違っている。ゴメン。でも直さない。[/追記]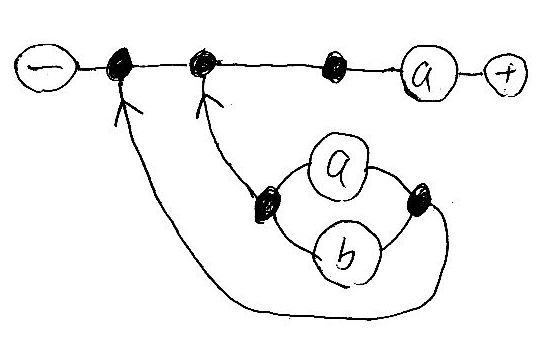） レイアウトを変更する（つながり具合は変更しない！）ときは、記号ノードを持たないワイヤーを使います。このような単なるワイヤーを、記号的にはε（イプシロン）とかI（大文字アイ）で示します((空列をモノイドの単位元、または圏の恒等と考えるときは、「1に似たI」がふさわしいでしょう。

*7:正確に言えば、空列だけからなる言語が、言語の連接演算の単位になっているってことです。

*8:山田尚勇（やまだ・ひさお）氏、2008年5月18日ご逝去

*9:while ((c = getchar()) != EOF) なんてイディオムが染み付いているせいでしょう。