「コンパクト閉圏と絵算で理解する線形代数とシーケント計算(入り口だけ)」において、アブラムスキーのネーム/コネームの話をしました。もう少し一般的な文脈では、射fのネームの仲間は4種類あります。それぞろを、∩f、f∩、∪f、 f∪ と書きましょう。絵で描けば次のとおり。
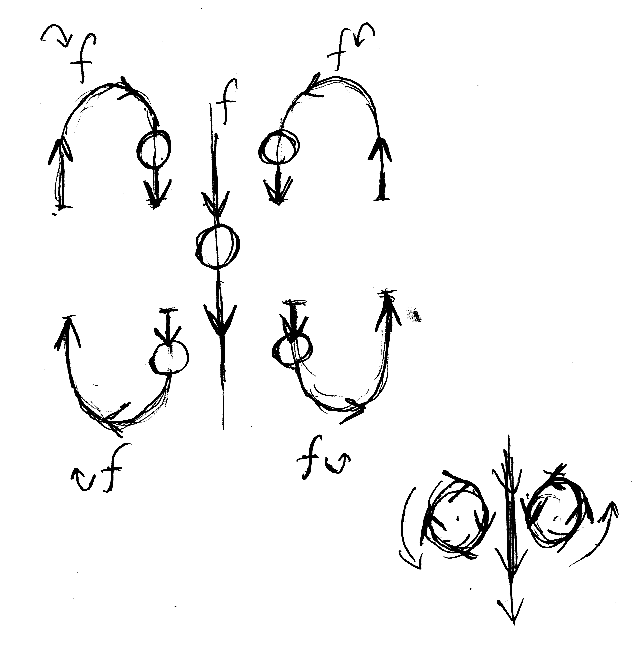
絵では、上下左右の添字にしている∩、∪に方向(矢印)も付けています。絵全体の印象は右下の小さな絵を見てください。[追記 dateTime="2010-12-24T08:18:37"]ウゲ、小さい絵の左側の回転方向が間違っている、逆だわ。左側は時計回りです。[/追記]
∩f がfのネーム、f∪ がfのコネームでした。f∩、∪f はなんて呼びましょう? 図の左右の入れ替えを「反」(op)という形容詞を付けて表現するとして、反ネーム(opname)、反コネーム(opconame)(またはコ反ネーム(coopname))とでもしましょう。
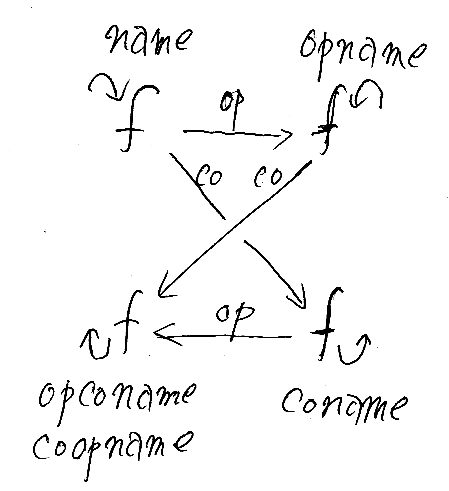
*AはAの左双対、A*はAの右双対です。左右の双対に関しては、「双対と随伴、そして左と右」を参照してください。
恒等射 A = idA:A→A に対して、4種のネーム類は次のようになります。
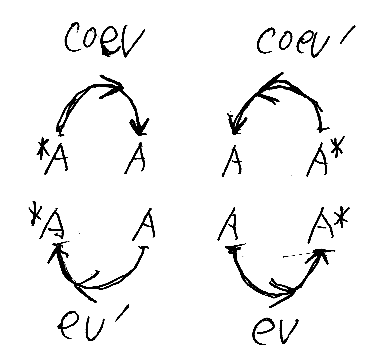
いろいろな呼び名がありますが、ここでは次のようにしました。
- coev := ∩A = (A = idAのネーム)
- coev' := A∩ = (A = idAの反ネーム)
- ev := A∪ = (A = idAのコネーム)
- ev' := ∪A = (A = idAの反ネーム)
線形代数などでは、ev(非退化双線形形式に対応)とcoev(正則行列に対応)だけで済んでしまうのは、ベースとなる圏において、左右の双対を区別する必要がなく、対称(symmetry)が存在するからです。例えば、coev'は、coevと対称σ = σA*,A の組み合わせで次のように記述できます。
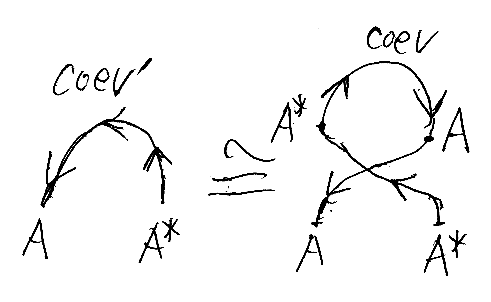
対称σによる同型をフリップ同型と呼ぶこともあります。対称σの代わりにブレイディングβ+、β-を使うと事情が少し複雑になりますが、同様なフリップ同型を定義できます。
ここらの話は、物理における粒子の対生成、対消滅、スワップと対応しているらしいのですが、僕にはよくわかりません。計算の議論としては、平面ラムダ計算に対応するようです。自己関手と自然変換の圏などでは、対称やブレイディングが存在するとは限らないので、左右を区別して4種のネーム類を考える必要があります。面白いような面倒なような……