また、「よくわからんわー」という愚痴みたいなハナシ。
記号の約束
Catを、小さい圏と関手からなる圏だとします。同様に、BiCatは小さい双圏と双圏のあいだの準同型*1からなる圏です。Catは厳密2-圏(特別な双圏)の構造を持ち、BiCatは3-圏の構造まで持ったりするようです(3次元の圏は僕よく知りません)。
Set、Cat、BiCat などを集合として含むようなもっと大きな宇宙(universe; 普遍領域)を考えて、その宇宙のなかの小さな圏の全体をCATとします。Set、Cat、BiCat などは、おおきな宇宙のなかでは集合なので、CAT(Cat, Set) などもおおきな宇宙のなかでは把握可能/取り扱い可能です(おおきな宇宙内でも、圏CATが小さいとは保証できませんが)。BICATも同様に、外側のおおきな宇宙で考えた双圏の圏です。
実際のところ、サイズ問題の扱い方はよくわからないのですが、とりあえず上記の二段階の宇宙で考えることにします。
圏の米田の補題
米田の補題から導かれる米田埋め込みでは、圏Cをその前層の圏に埋め込みます。C上の前層の圏は、CAT(Cop, Set) とCATのホムセットとして書けます。CATがデカルト閉*2で、内部ホム(指数、ベキ)があるので、CAT(Cop, Set) を表現する内部ホムを [Cop, Set] と書くと、この内部ホムは圏CATの対象として確定します。
Cの米田埋め込みは、yC:C→[Cop, Set] in CAT という関手で、次のように定義されます。
- yC(A) := C(-, A)
- yC(f:A→B) := (f*::C(-, A)⇒C(-, B))
f*は自然変換で、φ := f* = yC(f) と置くと、φの成分は次のように書けます。
- φX:C(X, A)→C(X, B), φX(g) := g;f
関手 yC:C→[Cop, Set] が充満忠実であることは、米田の補題の帰結のひとつです。
双圏の米田の補題
双圏に関する米田の補題から導かれる2次元版米田埋め込みは、Bを(小さな)双圏だとして、Bを [Bop, Cat]bi に埋め込む形をしているようです。[Bop, Cat]bi は、ホムセット BICAT(Bop, Cat) の内部化です。ここで、Catを双圏とみなして、双圏の準同型の全体が BICAT(Bop, Cat) です。内部化した [Bop, Cat]bi は、圏BICATの対象なので、これ自体双圏です。
双圏に関する米田の補題から、B→[Bop, Cat]bi が実際に埋め込みであることがわかり、任意の双圏は、2次の前層からなる双圏の部分双圏とみなしていいことになります。
具体的な計算は、Igor Bakovic "Bicategorical Yoneda lemma"にあります。図式が山盛りで、追いかけるには根性が要りますね。根性なしの僕には無理だ。
簡易版の2-Yoneda
以上に触れたように、双圏に関する立派な米田の補題があるのですが、立派過ぎて僕にはとても使えません。もうちょっと簡易版というか、特殊な状況で形が簡単になる米田スタイルの補題が欲しいのです。特殊な状況なので、一般性はなくなりますし、特殊な状況としての適用可能性条件も必要になります
で、どんな形の簡易版2-Yonedaが欲しいのかを以下に述べます。いつものように、計算モデルの圏で出会った状況から「欲しい」と思ったものです。
だったらいいな
ほんとはup-to-isoで考えるべきでしょうが、話が複雑になるので、on-the-nose(strict)の状況で述べます。つまり、一般の双圏ではなくて、Cat豊饒圏で考えます*3。以下、圏の直積をモノイド積、自明な圏1(対象1個、射も1個)をモノイド単位として、Cat = (Cat, 1, ×) をモノイド圏と考えます。
BはCat豊饒圏とします。つまり、B0= |B| を対象(0セル)の集合として、A, B∈B0 に対するB(A, B)が(小さい)圏になっています。そして、結合(composition)を与える双関手 compA,B,C:B(A, B)×B(B, C)→B(A, C) と恒等を与える関手 idA:1→B(A, A) が適切に与えられているとします。
ホム圏B(A, B)内の対象(1セル)は、f, gなどの記号で表し、ホム圏B(A, B)内の射(2セル)は、α、βなどとします。ホム圏内の射=2セルの結合はいつものとおり「;」を使い、compで与えられる結合のほうはスター積とも呼び、二項演算子記号「*」で表すことにします。順序は左から右/上から下の図式順(diagrammatic order)です。
α;β は2セルのホム圏内の結合=縦結合、α*γは2セルの横結合です。
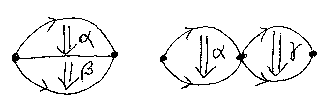
α::f⇒g, β::g⇒h、γ::j⇒k ならば、α;β::f⇒h、α*γ::f*j⇒g*k となります。
Bの0セルと1セルからなる圏をB1とします。|B1| = B0、B1(A, B) = |B(A, B)| となり、射の結合は横結合「*」で与えられます。B1は普通の(1次元の)圏です。B1は2次元の圏Bから2セルを取り除いた1次元骨格ですね。
さて本題; 2次元の圏Bからインデックスされた圏(indexed category)を作って、さらにインデックスされた関手と自然変換を考えて、それに関して米田の補題(の類似)が成立しているといいな、ってことです。この「いいな」はご都合主義な期待なので、一般的には成立してないでしょう。特定状況では成立しそうな状況証拠はあります。どんな条件なら成立するか/しないか? が知りたいのです。
まず、Bから、B1をベースとするインデックス付き圏を構成しましょう。A∈B0 を固定して、X∈B0 ごとに B(X, A)∈|Cat| を対応させます。つまり、次のような対応を作ります。
- B(-, A) = λX∈|B1|.B(X, A)∈|Cat|
f = (f:X→Y)∈B1(X, Y) に対しては、B(Y, A)→B(X, A) という関手が、fのpre-composeにより定義できます。これを、B(f:X→Y, A):B(Y, A)→B(X, A) と書きましょう。これもラムダ風に書くと:
- B(-, A) = λf∈B1(X, Y).B(f:X→Y, A)∈Cat(B(Y, A), B(X, A))
B(-, A) は、B1上で定義されてCatに値を持つ反変関手になるので、B1をベースとするインデックス付き圏となります。同様にして、B(A, -) は、B1をベースとする余インデックス付き圏となります。B(-, A) でも B(A, -) でも同じなので、B(-, A) のほうで考えることにします。
B(-, A) は、B1op→Cat という関手です(つまりインデックス付き圏)。f:A→B in B1 があると、fの後結合(post-composition)により B(-, A)⇒B(-, B) という自然変換ができます。
- f*::B(-, A)⇒B(-, B)
以上の定義は、通常の米田の補題/埋め込みとほとんど同様で、集合(Set)が圏(Cat)に置き換わるだけです。一般的な双圏のような複雑な構成は出て来ません。
この状況で、適当な条件を付ければ B→[B1, Cat] が圏同値の意味で埋め込み(擬埋め込みと呼べばいいのでしょうか)になっているといいな、というのが僕の期待です。Bの対象(0セル)Aに対して、関手 B(-, A) を A* のように略記すると、B(A, B) と [B1, Cat](A*, B*) は圏同値になります(なるといいな、ですが)。この圏同値は(もしそれがあれば)、アイレンベルグ(アイレンベルク)/ウォッツ(Eilenberg-Watts)*4の定理に相当するんじゃないか、と思えるのですが … はてさて?