モノイド圏と加群圏に関するフォークロアとマックレーン五角形・三角形

Cがモノイド圏でDが圏のとき、二項関手（双関手） H:C×D→D が結合律と単位律を満たすならば、(D, H)をC上の加群圏（module category）と呼びます。（加群の圏（category of modules）とは違いますから注意。）

モノイド圏C上の加群圏(D, H)と、モノイド関手 Φ:C→End(D) が同じであることは、圏論のフォークロアのひとつでしょう。フォークロアとは、誰かの発見と特定できるようなものではなく、なんとなく知られている事実のことです。

このフォークロアを律儀に確認してみます。その過程で、モノイド積やモノイド作用に関するマックレーン五角形・三角形の別解釈が得られます。

内容：

モノイド圏上の加群圏
左作用に関する一貫性
自己関手圏
二項関手のカリー化
左作用から高階関手の構成
モノイド関手
加群圏構造からモノイド関手を構成する
計算の準備
モノイド関手の結合律とマックレーン五角形
モノイド関手の単位律とマックレーン三角形
加群圏の左作用と表現モノイド関手の対応
フォークロアが教えてくれること

モノイド圏上の加群圏

C = (C, $\otimes$ , I, α, λ, ρ) をモノイド圏（monoidal category）とします。α, λ, ρは、モノイド積 $\otimes$ の結合律と左右の単位律を与える自然同型です*1。二項関手 H:C×D→D を、中置演算子記号 $\odot$ でも表すことにします。 $\odot$ が次の性質を持つとき、 $\odot$ を“モノイド圏Cの圏Dへの左作用（left action）”と呼びます。

A, B∈|C|、X∈|D| に対して、(A $\otimes$ B) $\odot$ X $\stackrel{\sim}{=}$ A $\odot$ (B $\odot$ X)
I $\odot$ X $\stackrel{\sim}{=}$ X

一番目を左作用の結合律、二番目を左作用の単位律と呼びます。

上記の定義は大雑把なもので、より精密な定義は後でします。とりあえず、モノイド圏Cによる左作用を持つ圏を、C上の左加群圏（left module category）と呼びます。この記事では左作用／左加群圏しか出てこない（右は扱わない）ので、左作用／左加群圏を単に作用／加群圏と言うこともあります。

“モノイド圏による作用＝加群圏”に関しては、WikipediaでもnLabでも矢鱈に雑な説明しかされていません。

モノイド圏作用（monoidal category action）、モノイド圏加群（monoidal category module）なんて名前もあるんだな、と分かる程度ですね。参考文献や起源に関しては、次のpantodonページがまとまっています。

http://pantodon.shinshu-u.ac.jp/topology/literature/monoidal_category_module.html

余談ですが、言葉について注意を付け加えておくと；加群圏（module category）は、加群の圏（category of modules）とは違います。ところが、加群の圏を加群圏と呼ぶこともあるので紛らわしい！「モノイド圏」の場合、英語では"monoidal"と語尾が"-al"で終わる形容詞が使われていますが、modular category（モジュラー圏）は既に別な意味で使われているし、mudulalという形容詞はないようです。結局、名詞module（加群）をそのまま形容詞にも使っています。

日本語だと、"-al"に相当する（と思われる）「的」を付けて「加群的圏」もありますが、鬱陶しい感じがするので「的」は付けませんでした。"-al"とか「的」で形容詞らしくするって方法を一貫するのも難しいので、もういいや、と思ってます。例えば、環的／半環的な圏を ringal/semiringal category と呼ぶほうが好ましいでしょうが、最近は ring/semiring category も目にします。モノグサな僕は、名詞をそのまま形容詞に使う用法のほうがラクチンで好きです。

左作用に関する一貫性

前節で述べた左作用の結合律と単位律を再掲すると：

A, B∈|C|、X∈|D| に対して、(A $\otimes$ B) $\odot$ X $\stackrel{\sim}{=}$ A $\odot$ (B $\odot$ X)
I $\odot$ X $\stackrel{\sim}{=}$ X

この同型を与える可逆射を、それぞれα'_A,B,X、λ'_Xとします。

α'_A,B,X:(A $\otimes$ B) $\odot$ X→A $\odot$ (B $\odot$ X)
λ'_X:I $\odot$ X→X

ダッシュ（プライム）を付けているのは、モノイド圏Cのモノイド積 $\otimes$ に関するα、λと区別するためです。

α、λ、ρに関しては、マックレーンの五角形図式と三角形図式が可換であることが要求されます（モノイド圏の一貫性の要求）。同様に、α'、λ'に関しても五角形図式と三角形図式の可換性を要求します。ただし、図式はα'、λ'だけで構成されるのではなくて、α、λ、ρも混じった図式です。

五角形図式／三角形図式が可換であることを、もう少し説明しましょう。

A, B, C∈|C| と X∈|D| を $\otimes$ または $\odot$ をあいだに挟んで並べると、いくつかの記号列が得られます。これらの記号列は、括弧の付け方のバリエーションを列挙したものです。

見やすくするために、 $\otimes$ も $\odot$ も省略して単なる併置でモノイド積と左作用を表すことにしてます。例えば、(A B) (C X) は (A $\otimes$ B) $\odot$ (C $\odot$ X) です。括弧付けのバリエーションを書き並べると：

A (B (C X))
(A B) (C X)
((A B) C) X
(A (B C)) X
A ((B C) X)

これら5つのバリエーションのあいだを、α、α'、恒等射の組み合わせで繋ぐと五角形になります。これから先では、その五角形の可換性を要求するわけです。左作用に関する五角形は、モノイド積に対する五角形とほぼ同じなので、次の記事の絵も参照してください。

単位律に関して言うと、次の3つで可換な三角形を作ります。

A X
I (A X)
(I A) X

もうひとつの三角形があります。

A X
A (I X)
(A I) X

上記の2つの三角形が可換になることも要求します。

五角形・三角形の図式は今ここでは描きませんが、後で出てきます（五角形、三角形）。

自己関手圏

Dを圏とします。Dはモノイド構造を持つ必要はなくて、単なる圏で十分です。D上の自己関手の圏をEnd(D)と書くことにします。End(D)は、モナドの話でも登場する重要な圏です*2。

End(D)の射は自己関手のあいだの自然変換であり、自然変換の縦結合で圏となります。さらに、自己関手の結合と自然変換の横結合をモノイド積と考えて非対称なモノイド圏となります。End(D)をEと略記して説明すると：

Eの対象は、F:D→D という自己関手である。
F, GをEの対象（自己関手）として、FからGへの射は、自然変換 α::F⇒G:D→D である。
α::F⇒G, β::G⇒G' をEの射（自然変換）として、αとβの結合は、自然変換の縦結合 α;β::F⇒G' である。
恒等射は、関手に対する恒等自然変換である。
F, GをEの対象として、FとGのモノイド積は、関手の結合 F*G である（「*」は、図式順の結合を表す記号）。
α::F⇒G, β::F'⇒G' をEの射（自然変換）として、αとβのモノイド積は、自然変換の横結合 α*β::F*F'⇒G*G' である。
モノイド単位は、Dの恒等関手である。

ここで、アスタリスク記号「*」を、関手の図式順結合と自然変換の図式順横結合の意味で使いました。反図式順の結合と横結合には、「 $\circ$ 」を使うことにします。G $\circ$ F = F*G、β $\circ$ α = α*β です。

僕は反図式順を嫌っていますが、今回の話では反図式順のほうが便利なので、反図式順記法も使うことにします。

二項関手のカリー化

今回話題にしているフォークロアは、“モノイド圏C上の加群圏D”と、“CからEnd(D)へのモノイド関手”が1：1に対応する、というものです。この主張の背後には、モノイド構造を無視した状況で、二項関手と高階関手*3が1：1に対応する事実があります。

上記の1：1対応は、「圏の圏Catがデカルト閉圏である」ことに由来します。X, Y, Zが圏のとき、一般に次の同型が存在します。

Cat(X×Y, Z) $\stackrel{\sim}{=}$ Cat(X, [Y, Z])

ここで、[Y, Z]は関手圏を表します。つまり、X×Y→Z という形の二項関手（双関手）と、X→[Y, Z] という形の高階関手が1：1に対応するのです。これは、関手のカリー化／反カリー化に他なりません。

X = C、Y = Z = D と置いみると：

Cat(C×D, D) $\stackrel{\sim}{=}$ Cat(C, [D, D])

C×D→D という二項関手と、C→End(D) という高階関手がカリー対応することになります。

モノイド圏C上の加群圏の実質は、左作用を与える二項関手 H:C×D→D ですから、これをカリー化すると、高階関手 Φ:C→End(D) が得られます。逆に、高階関手Φから二項関手Hを作ることもできます。

問題となるのは、Hの結合性／単位性／一貫性とΦのモノイド関手性（これも結合性／単位性）がキチンと対応するかどうかです。

左作用から高階関手の構成

モノイド圏C上の加群圏(D, H)があったとして、二項関手 H:C×D→D から高階関手 Φ:C→End(C) を構成しましょう。とりあえずCのモノイド構造は忘れて、二項関手Hのカリー化から始めます。H(-, -) と - $\odot$ - は同じ意味です。

Cの対象Aをひとつ取ってきて、F_A:D→D を定義します。

F_A(X) := A $\odot$ X
F_A(f:X→Y) := (A $\odot$ f:A $\odot$ X→A $\odot$ Y)

A $\odot$ fは、正確には id_A $\odot$ f ですが、対象Aと恒等射id_Aは同一視することにします。

F_AがD上の自己関手であることは容易に確認できるので、A|→F_A が |C|→|End(D)| という対応を定義することが分かります。一般的に、二項関手の片一方の変項を固定すると、残った変項に関する単項関手（普通の関手）が得られます。

次に、f:A→B をCの射とします。fに対して、自然変換 φ::F_A⇒F_B:D→D を定義しましょう。自然変換はその成分で決まるので：

φ_X := H(f, X)

より具体的に書くと：

φ_X := f $\odot$ X : A $\odot$ X→B $\odot$ Y in D

φが自然変換であることは、一般論からも出ますが、具体的な表示を使って書きましょう。u:X→Y をDの射として、次の図式が可換になればいいわけです。

AX -φ_X→ BX
｜　　　　　｜
Au　　　　Bu
↓　　　　　↓
AY -φ_Y→ BY

φの定義を展開すると、この図式の可換性は、次の等式となります。

(A $\odot$ u);(f $\odot$ Y) = (f $\odot$ X);(B $\odot$ u)

これは、H（= $\odot$ ）が二項関手（双関手）であることからの帰結ですが、 $\odot$ に関する交替律（interchange law）とみなせます

自然変換φは、Cの射fから決まるので、φ = Φ(f) と書くことにします。記号を合わせるために、Φ(A) = F_A、Φ(B) = F_B と置きます。すると、Cの射 f:A→B から、自然変換 Φ(f):Φ(A)→Φ(B) in End(D) が決まることになります。次の等式の成立も図式か等式の計算で出ます。

Φ(f;g) = Φ(f);Φ(g) （右辺は自然変換の縦結合）
Φ(id_A) = ι_Φ(A) （ι_Fは、関手Fの恒等自然変換）

以上で、HからΦが作れました。しかし、Cがモノイド圏であることは何も使ってないので、Φがモノイド関手になる（モノイド関手に出来る）保証は、今この時点ではありません。

モノイド関手

モノイド関手（とラックスモノイド関手）については、次の記事で説明しています。

ここでは、用語と記法を確認するだけにします。

二項関手 H:C×D→D からの関手カリー化により、高階関手 Φ:C→End(D) が得られました。HとΦの関係は、大雑把に言えば、Φ(A)(X) := H(A, X) = A $\odot$ X です。

Cにはモノイド構造 (C, $\otimes$ , I)、End(D)にもモノイド構造 (End(C), $\circ$ , Id) があります（ $\circ$ は反図式順結合、IdはDの恒等関手）。これらのモノイド構造に関して、Φがモノイド関手になるかどうかが問題です。

モノイド関手の定義には、台となる関手だけではなくて、自然同型μとεが必要でした（「モノイド関手／ラックス・モノイド関手とその実例」参照）。μをモノイド関手乗法、εをモノイド関手単位と呼ぶことにします。台関手がΦであるモノイド関手乗法、モノイド関手単位とは次のようなものです。

A, B∈|C| に対して、μ_A,B:Φ(A) $\circ$ Φ(B)→Φ(A $\otimes$ B) in D
ε:Id→Φ(I) in D

Φ, μ, εが従うべき法則は、モノイド関手の結合律と左右の単位律です。これらの法則に関しては「モノイド関手／ラックス・モノイド関手とその実例」を参照してください、マッカーディのストライプ図による説明があります。

加群圏構造からモノイド関手を構成する

台関手 Φ:C→End(D) 上にモノイド関手としての構造を与えましょう。Cはモノイド圏で、Dへの左作用を持ちました。それらの前提を使ってΦをモノイド関手に仕立てます。

End(D)の射 μ_A,B:Φ(A) $\circ$ Φ(B)→Φ(A $\otimes$ B) は自然変換なので、自然変換らしく書けば μ_A,B::Φ(A) $\circ$ Φ(B)⇒Φ(A $\otimes$ B):D→D です。自然変換μ_A,BのX-成分（X∈|D|）は次のように書けます。

(μ_A,B)_X:(Φ(A) $\circ$ Φ(B))(X)→(Φ(A $\otimes$ B))(X)

記号 $\odot$ を使って書けば：

(μ_A,B)_X:A $\odot$ (B $\odot$ X)→(A $\otimes$ B) $\odot$ X

この形を見れば、(μ_A,B)_Xをどう定義すべきか見当はつくでしょう。

(μ_A,B)_X := (α'_A,B,X)^-1 : A $\odot$ (B $\odot$ X)→(A $\otimes$ B) $\odot$ X

α'が自然同型だったので、成分ごとに可逆で、α'^-1を作れるわけです。最初からα'の向きを逆にしておけば、逆射を取る必要もなかったですけどね。

モノイド関手の単位 ε::Id⇒Φ(I) も同様な考察から：

ε_X := (λ'_X)^-1 : X→I $\odot$ X

これで、(Φ, μ, ε) という三つ組が揃いました。あとは、(Φ, μ, ε) がモノイド関手の結合律、左右の単位律を満たすことを確認する計算です。

計算の準備

モノイド関手の結合律と左右の単位律を計算で示せばいいのですが、このテの計算は、難しくはないけど手間がかかるもんです。前もって手順を考えて、幾つかの準備をしておきます。

僕は、ペースティング図の可換性を追いかける方法が苦手なので、マッカーディ（Micah Blake McCurdy）のストライプ図と等式的記号計算を組み合わせた次の手順を採用します。

モノイド関手の結合律と左右の単位律に対するマッカーディのストライプ図を描く。
ストライプ図を見ながら記号的表現に置き換える。
マックレーンの五角形、三角形に帰着させる。

ストライプ図と記号的表現の対応を取るために、いくつか約束をしておきます。

結合律（Associative law）をAs, 左単位律（Left Unit law）をLU、右単位律（Right Unit law）をRUと略記する。
それぞれの法則の左辺は接尾辞L、右辺は接尾辞Rを付けて表す。詳しくは：
1. 結合律の左辺はAsL、右辺はAsR
2. 左単位律の左辺はLUL、右辺はLUR
3. 右単位律の左辺はRUL、右辺はRUR
ストライプ図のなかに何本かの水平な“水準線”を引く。
水準線には上から順に番号を付ける。AsL1, AsL2など。

各水準線ごとに記号表現に置き換えます（次節で実際にやります）。

左単位律の自然同型に小文字ラムダを使ってしまったので、ラムダ式「λ変数.式」の代わりに、「(変数|式)」の形をラムダ抽象として使います。例えば、(X|(A $\otimes$ B) $\odot$ X)。

圏の射に関する等式を、左右ではなくて上下に書くことがあります。例えば、f;g = h という等式を、次の形に書きます。

   A -(f)→ B -(g)→ C
  ====================
   A -(h)→ C

この図の意味は「上段の射のチェーンを結合したものと、下段の射のチェーンを結合したものが等しい」ということです。

モノイド関手の結合律とマックレーン五角形

まずは、マッカーディのストライプ図。描画方向は ↓→ です。旗で示すならば：

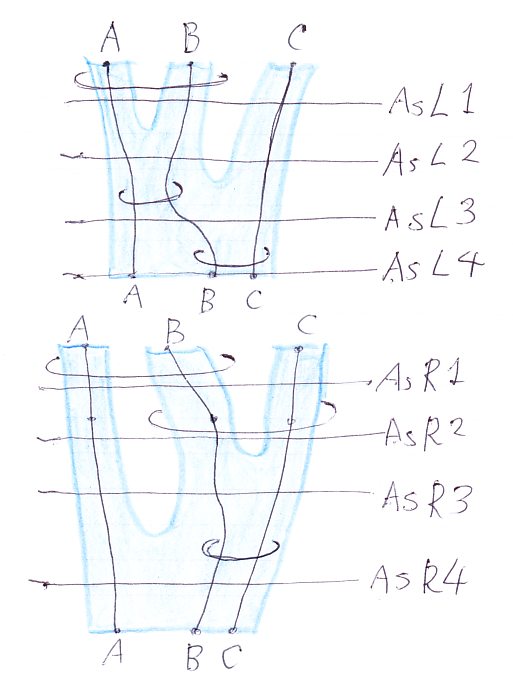
各水準線ごとに記号表現に置き換えます。

AsL1: (Φ(A) $\circ$ Φ(B)) $\circ$ Φ(C)
AsL2: Φ(A $\otimes$ B) $\circ$ Φ(C)
AsL3: Φ((A $\otimes$ B) $\otimes$ C)
AsL4: Φ(A $\otimes$ (B $\otimes$ C))

前節で説明したラムダ式の構文を使ってより具体的に書き下せば：

AsL1: ((Z|A $\odot$ Z) $\circ$ (Y|B $\odot$ Y)) $\circ$ (X|C $\odot$ X) =
(X|A $\odot$ (B $\odot$ (C $\odot$ X)))
AsL2: (Y|(A $\otimes$ B) $\odot$ Y) $\circ$ (X|C $\odot$ X) =
(X|(A $\otimes$ B) $\odot$ (C $\odot$ X))
AsL3: (X|((A $\otimes$ B) $\otimes$ C) $\odot$ X)
AsL4: (X|(A $\otimes$ (B $\otimes$ C)) $\odot$ X)

ラムダ式にDの対象Xを適用して、各水準線のあいだを縦に繋ぐ射を書き下します。

AsL1→AsL2: (α'_A,B,CX)^-1 : A $\odot$ (B $\odot$ (C $\odot$ X)) → (A $\otimes$ B) $\odot$ (C $\odot$ X)
AsL2→AsL3: (α'_AB,C,X)^-1 : (A $\otimes$ B) $\odot$ (C $\odot$ X) → ((A $\otimes$ B) $\otimes$ C) $\odot$ X
AsL3→AsL4: α_A,B,C $\odot$ X : ((A $\otimes$ B) $\otimes$ C) $\odot$ X → (A $\otimes$ (B $\otimes$ C)) $\odot$ X

すべての射を並べたチェーンは次のように書けます。

AsL1 -((α'_A,B,CX)^-1)→ AsL2 -((α'_AB,C,X)^-1)→ AsL3 -(α_A,B,C $\odot$ X)→ AsL4

次は右辺です。

AsR1: (Φ(A) $\circ$ Φ(B)) $\circ$ Φ(C)
AsR2: Φ(A) $\circ$ (Φ(B) $\circ$ Φ(C))
AsR3: Φ(A) $\circ$ Φ(B $\otimes$ C)
AsR4: Φ(A $\otimes$ (B $\otimes$ C))

ラムダ式で表現：

AsR1: ((Z|A $\odot$ Z) $\circ$ (Y|B $\odot$ Y)) $\circ$ (X|C $\odot$ X) =
(X|A $\odot$ (B $\odot$ (C $\odot$ X)))
AsR2: (Z|A $\odot$ Z) $\circ$ ((Y|B $\odot$ Y) $\circ$ (X|C $\odot$ X)) =
(X|A $\odot$ (B $\odot$ (C $\odot$ X)))
AsR3: (Y|A $\otimes$ Y) $\circ$ (X|(B $\otimes$ C) $\odot$ X) =
(X|A $\odot$ ((B $\otimes$ C) $\odot$ X))
AsR4: (X|(A $\otimes$ (B $\otimes$ C)) $\odot$ X)

各水準線のあいだを繋ぐ射は：

AsR1→AsR2: id : A $\odot$ (B $\odot$ (C $\odot$ X)) → A $\odot$ (B $\odot$ (C $\odot$ X))
AsR2→AsR3: A $\odot$ (α'_B,C,X)^-1 : A $\odot$ (B $\odot$ (C $\odot$ X)) → A $\odot$ ((B $\otimes$ C) $\odot$ X)
AsR3→AsR4: (α'_A,BC,X)^-1 : A $\odot$ ((B $\otimes$ C) $\odot$ X) → (A $\otimes$ (B $\otimes$ C)) $\odot$ X

射のチェーンは：

AsR1 -(id)→ AsR2 -(A $\odot$ (α'_B,C,X)^-1)→ AsR3 -((α'_A,BC,X)^-1)→ AsR4

AsL1 = AsR1 = AsR2、AsL4 = AsR4 に注意して番号を振り直します。

AsL1 = AsR1 = AsR2 : A $\odot$ (B $\odot$ (C $\odot$ X))
AsL2 : (A $\otimes$ B) $\odot$ (C $\odot$ X)
AsL3 : ((A $\otimes$ B) $\otimes$ C) $\odot$ X
AsL4 = AsR4 : (A $\otimes$ (B $\otimes$ C)) $\odot$ X
AsR3 : A $\odot$ ((B $\otimes$ C) $\odot$ X)

この番号で、モノイド関手に関する結合律を等式として書くと：

 (1)-((α'_A,B,CX)^-1)→(2)-((α'_AB,C,X)^-1)→(3)-(α_A,B,CX)→(4)
 ==============================================================
 (1)-(A(α'_B,C,X)^-1)→(5)-((α'_A,BC,X)^-1)→(4)

これが、モノイド関手の結合律ですが、可換図式の形に書き換えると、左作用に関するマックレーンの五角形になります。

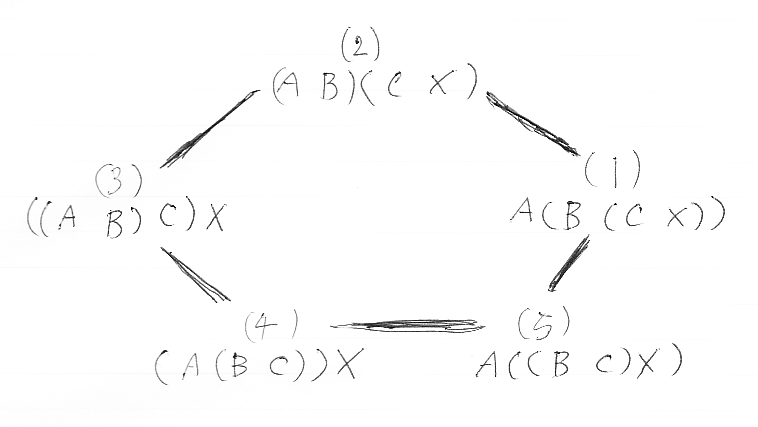
先の等式（上段・下段の図）は、(1)→(2)→(3)→(4) の経路と、(1)→(5)→(4) の経路が等しいことを主張してますが、普通の五角形等式は、(3)→(2)→(1) の経路と、(3)→(4)→(5)→(1) の経路が等しい形をしています。五角形の辺はすべて可逆なので、要するに「どこを通っても同じ」になっていれば何でもいいのです。

結局、「モノイド関手の結合律」と「左作用に関するマックレーンの五角形」は同値な条件だったのです。

モノイド関手の単位律とマックレーン三角形

モノイド関手の単位律には左と右がありますが、大差ないので、左単位律だけを示します。最初にマッカーディのストライプ図：

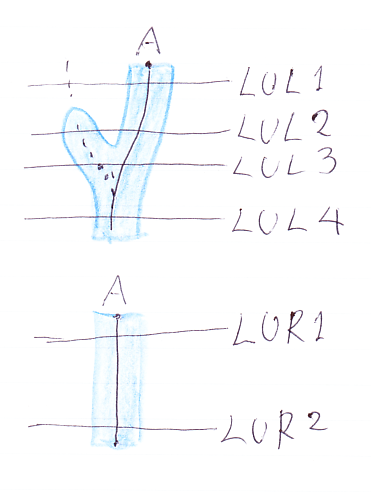
LUL1: Id $\circ$ Φ(A)
LUL2: Φ(I) $\circ$ Φ(A)
LUL3: Φ(I $\otimes$ A)
LUL4: Φ(A)

ラムダ式による表現：

LUL1: (Y|Y) $\circ$ (X|A $\odot$ X) =
(X|A $\odot$ X)
LUL2: (Y|I $\odot$ Y) $\circ$ (X|A $\odot$ X) =
(X|I $\odot$ (A $\odot$ X))
LUL3: (X|(I $\otimes$ A) $\odot$ X)
LUL4: (X|A $\odot$ X)

各水準線のあいだを繋ぐ射は：

LUL1→LUL2: (λ'_AX)^-1 : A $\odot$ X → I $\odot$ (A $\odot$ X)
LUL2→LUL3: (α'_I,A,X)^-1 : I $\odot$ (A $\odot$ X) → (I $\otimes$ A) $\odot$ X
LUL3→LUL4: λ_A $\odot$ X : (I $\otimes$ A) $\odot$ X → A $\odot$ X

射のチェーンは：

LUL1 -((λ'_AX)^-1)→ LUL2 -((α'_I,A,X)^-1)→ LUL3 -(λ_A $\odot$ X)→ LUL4

右辺は単純です。

LUR1: Φ(A) = (X|A $\odot$ X)
LUR2: Φ(A) = (X|A $\odot$ X)

射のチェーンは自明です。

LUR1 -(id)→ LUR2

LUL1 = LUL4 = LUR1 = LUR2 に注意して番号を振り直します。

LUL1 = LUL4 = LUR1 = LUR2 : A $\odot$ X
LUL2 : I $\odot$ (A $\odot$ X)
LUL3 : (I $\otimes$ A) $\odot$ X

等式は次の形になります。

 (1)-((λ'_AX)^-1)→(2)-((α'_I,A,X)^-1)→(3)-(λ_AX)→(1)
 ======================================================
 (1)-(id)→(1)

可換な三角形として描くと次のようになります。

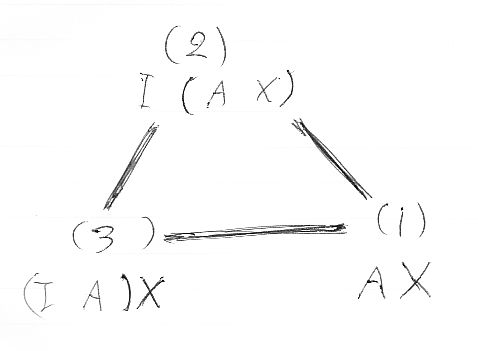
五角形のときと事情は同じで、どんな経路を通っても同じであることを主張しています。したがって、「モノイド関手の単位律」と「左作用に関するマックレーンの三角形」は同値な条件です。

加群圏の左作用と表現モノイド関手の対応

圏Dに対して、モノイド圏C上の左加群構造を与えているのは、左作用二項関手 H:C×D→D （H = $\odot$ ）です。Hから標準的に高階関手Φ:C→End(D) が構成できますが、ΦはCをD上の自己関手圏内に“表現”する関手です。群やモノイドの線形表現などとの類似があります。なので、Φは加群圏に付随する（Cの）表現モノイド関手と呼ぶことにします。

前節の計算から、加群圏の左作用と表現モノイド関手のあいだには次のような対応があることがわかります。

加群圏の左作用	表現モノイド関手
結合性自然同型 α'	モノイド関手乗法 μ
左単位性自然同型 λ'	モノイド関手単位 ε
マックレーンの五角形等式	モノイド関手結合律
マックレーンの三角形等式	モノイド関手単位律