一般化されたマイヒル／ネロードの定理 3：オートマトンの振る舞いと観測

ソフトウェアの設計と実装では、サブシステムやコンポネントの内部構造を明かすべきではない、と考えられています。アプリケーションプログラムは、サブシステム／コンポネントの公式のインターフェイスにだけ依拠すべきだ、となります。それを守れば、サブシステム／コンポネントの内部構造が変わっても（インターフェイスが不変なら）アプリケーションはそのまま動き続けるでしょう。

上記のような原則や、それからの帰結を一般化オートマトンの文脈で定式化してみます。

内容：

1. 隠蔽原則
2. 復習：構文と意味
3. 振る舞い
4. オートマトンの振る舞いと観測
5. 非退化指標／非退化オートマトン
6. 振る舞いの反カリー化表現と観測手順
7. リファクタリング補題と観測の関手性
8. 今回のまとめ

• 初回／ハブ記事

隠蔽原則

一般化オートマトンの典型的な例は、伝統的オートマトンや特定のインターフェイスに対する実装クラスなどです。これらのオートマトンは内部構造を持ちます。しかし、その内部構造を知ることは出来ないという仮定を置きます。この仮定を情報隠蔽原則（information hiding principle）、または単に隠蔽原則と呼びましょう。「実装の細部を利用者に漏らしてはならない」というアレです。

しかしですね、現実には内部構造（＝実装の詳細）が見えちゃうこともあるんですよね。なので、隠蔽原則は、「内部構造を知り得るにしても、それを利用してはならない」という利用者側の規範だと捉えるのが実際的でしょう。

我々の設定において知ってはいけない内部構造（実装の詳細）とは、オートマトンの状態空間のことです。F:Φ→Set がオートマトンのとき、xが隠蔽頂点ならF(x)は型xの状態空間です。そのようなF(x)がどんな集合であるかは何も分からないということです。状態空間F(x)の正体は完全に未知（不可知）なのですから、F(x)からの写像やF(x)への写像の正体もサッパリ分かりません。

一方で、xが可視頂点（x∈(S∪D)）なら、F(x)は既知の値空間であり、完全に理解できます。既知の値空間（例：整数値の空間、真偽値の空間）のあいだの関数もまた完全に理解できるとします。

徹底した隠蔽原則の支配下において、我々は何が出来るでしょうか？ -- この問題意識が、マイヒル／ネロードの定理の源泉です。そして、マイヒル／ネロードの定理が教えてくれる答は、「頑張れば、知りたいことは何でも分かる」です。

「頑張る」とは何をすることでしょう？ 「知りたいこと」とは何でしょう？ 今後、これらに正確な定義を与えていくことにします。

復習：構文と意味

「一般化されたマイヒル／ネロードの定理 2：文化的なギャップを乗り越えるための対訳表」で述べたように、このテの話題で最大の難関は言葉・用語法・記法の問題だと思います。もう一度言葉の一覧表を示しておきます。「くどい」と思われる方はこの節をスキップしてください。以下、Φ = (Φ, S, D), C = FreeCat(Φ), Hid = |Φ|＼(S∪D) です。

モノ	グラフ理論	圏論	形式的プログラム構文論	説明
|Φ|の要素	頂点	対象	ソート記号	型の名前
Φ(x, y)の要素	辺	（生成系の）射	オペレーション記号	基本手続きの名前
C(x, y)の要素	パス	射	オペレーション記号の列	プログラムコード
Dの要素	開始頂点	開始対象	開始ソート記号	コンストラクタの引数の型の名前
Sの要素	識別頂点	識別対象	識別ソート記号	クエリーの値の型の名前
D∪S の要素	可視頂点	可視対象	可視ソート記号	既知の型の名前
Hidの要素	隠蔽頂点	隠蔽対象	隠蔽ソート記号	不可知な型の名前
s∈S, x∈Hid として Φ(s, x)の要素	コストラクタ辺	コンストラクタ射	コンストラクタ記号	コンストラクタの名前
x∈Hid, d∈D として Φ(x, d)の要素	クエリー辺	クエリー射	クエリー記号	クエリーの名前
x, y∈Hid として Φ(x, y)の要素	コマンド辺	コマンド射	コマンド記号	コマンドの名前

これらは指標グラフΦ、指標圏Cに関連する概念で、すべては構文的存在物です。意味は、関手 F:C→Set によって与えられます。意味を与える関手Fがオートマトンそのものです。Fの行き先は集合圏なので、集合と写像の世界です。構文に対応する意味的存在物は次のように呼びます。

モノ	呼び名
x∈(D∪S) として F(x)	値空間
s∈S として F(s)	開始値空間
d∈D として F(d)	識別値空間
y∈Hid として F(y)	状態空間
s∈S, x∈Hid, c∈Φ(s, x) として F(c)	コストラクタ写像
d∈D, x∈Hid, q∈Φ(x, d) として F(q)	クエリー写像
x, y∈Hid, f∈Φ(x, y) として F(f)	コマンド写像

ΦやCに属するモノ（頂点、辺、パス）とSetに属するモノ（集合、写像）は徹底的に区別しましょう。そうでないと、話がワヤクチャになります。

例として、整数スタックの指標グラフを再掲します。（thisがマズかったなー、という話は「整数スタックの例」に追記で強調されてます。マズイけど、そのまま。）

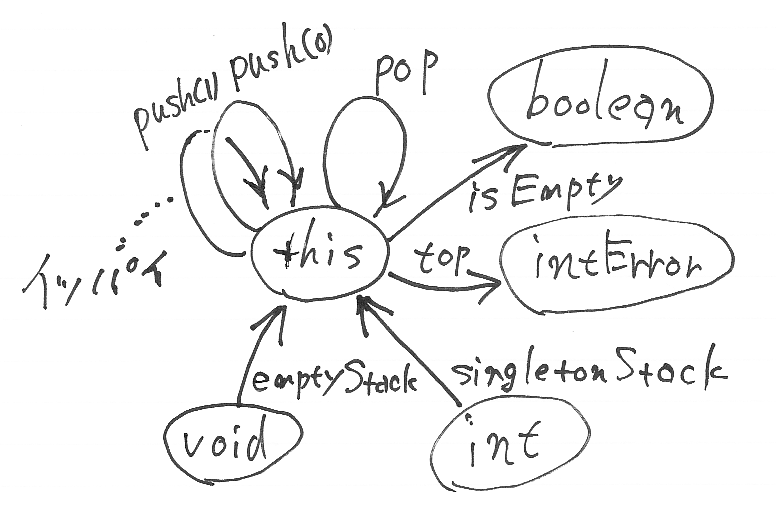
この例において：

• 開始頂点：{void, int}
• 識別頂点：{boolean, intError}
• 可視頂点：{void, int, boolean, intError}
• 隠蔽頂点：{this}
• コンストラクタ辺：{emptyStack, singletonStack}
• クエリー辺：{isEmpty, top}
• コマンド辺：{pop}∪{push(n) | n∈Z}

可視頂点には、前もって実際の集合が割当てられています。その割当ては固定化関手Kで行われます。

1. K(void) = 1 = {0}
2. K(int) = Z = {... -1, 0, 1, 2, ...}
3. K(boolean) = B = {true, false}
4. K(intError) = Z∪{error}

この例の指標をΨとして、オートマトン G:Ψ→Set を定義するとは、次のモノを決めることになります。

1. 集合 G(this)
2. 写像 G(emptyStack):1→G(this)
3. 写像 G(singletonStack):Z→G(this)
4. 写像 G(isEmpty):G(this)→B
5. 写像 G(top):G(this)→Z∪{error}
6. 写像 G(pop):G(this)→G(this)
7. n∈Zごとの写像 G(push(n)):G(this)→G(this)

数学的な記法ではなくて、実在のプログラミング言語でGを書き下してみましょう。TypeScriptを使ってみます。

// IntStack.ts

// intがないのでナンチャッテ定義
// 名前がintになっているだけ
type int = number;

class IntStack {
    private list_: int[]; // G(this) = List(Z) 隠蔽されている
    constructor() {
        this.list_ = [];
    }
    // メイヤー先生のクエリ
    isEmpty() : boolean {
        return (this.list_.length == 0);
    }
    top() : int {
        if (this.isEmpty()) {
            throw new Error("error");
        }
        return this.list_[this.list_.length - 1];
    }

    // メイヤー先生のコマンド
    pop() : void {
        if (this.isEmpty()){
            return; // ちと分かりにくいが、何もしない
        }
        this.list_.pop();
    }
    push(n : int) : void {
        this.list_.push(n);
    }

    // 生成子（コンストラクタ）
    // TypeScriptネイティブのコンストラクタを使って
    // static関数として実装
    static emptyStack() : IntStack {
        return new IntStack();
    }
    static singletonStack(n : int) : IntStack {
        var stk = new IntStack();
        stk.push(n);
        return stk;
    }
}

振る舞い

Φ = (Φ, S, D), K:Φ_vis→Setとして、部分固定指標Φ/Kに対して、振る舞いと呼ばれるモノを定義します。振る舞い（behavior, behaviour）とは、s∈D, d∈D で添字付けられた写像の族 b_{s, d}:C(s, d)→Set(K(s), K(d)) のことです。ここで、C = FreeCat(Φ) です。振る舞いは英字小文字ボールド体で示すことにします -- a, b などは指標グラフΦの辺、指標圏Cの射を表すことがあるので区別したいのです。

伝統的オートマトンの部分固定指標Φ/Kについて、その振る舞いを見てみます。Φ/Kが伝統的オートマトンの部分固定指標なら、|Φ| = {0, 1, 2}, S = {0}, D = {2}, Φ(0, 1) = {i}, Φ(1, 1) = Γ, Φ(1, 2) = {t}, K(0) = 1, K(2) = B となります。振る舞いは b_{0, 2} だけで決まるので、b_{0, 2}を単にbと書きます。

振る舞いの定義より、b:C(0, 2)→Set(1, B) という写像です。C(0, 2) C(1, 1) = Γ^* です。Γ = Φ(1, 1) で、Γ^* はΓのクリーネスターです。一方、Set(1, B) B なので、結局 b:Γ^*→B とみなしてかまいません。

b:Γ^*→B に対して、b^-1(true) はΓ^* の部分集合です。逆にΓ^* の部分集合から、写像 Γ^*→B が決まります。Γ^* の部分集合とは、アルファベットΓの形式言語に他なりません。つまり、伝統的オートマトンにおける振る舞いと形式言語は1：1対応するのです。

部分固定指標Φ/Kに対して、その振る舞いの全体からなる集合をBeh[Φ/K]とします。Φ/Kが伝統的オートマトンの部分固定指標の場合は、上で述べたとおり、Beh[Φ/K]はアルファベットΓ上の言語の集合と同じものです。Γ上のすべての形式言語からなる集合をLang(Γ)とすると、

• 伝統的オートマトンでは、Beh[Φ/K] Lang(Γ) 。

整数スタックの例では、振る舞いbは次の写像達からなります。

1. b_{void, boolean}:C(void, boolean)→Set(1, B)
2. b_{void, intError}:C(void, intError)→Set(1, Z∪{error})
3. b_{int, boolean}:C(int, boolean)→Set(Z, B)
4. b_{int, intError}:C(int, intError)→Set(Z,Z∪{error})

b_{int, intError}の値の実例を幾つか出しましょう。次のパス（Cの射はΦのパス）を取ります。

1. singletonStack;top
2. singletonStack;push(2);push(3);top
3. singletonStack;pop;top

これらのパスに対する値は：

1. b_{int, intError}(singletonStack;top) = λn∈Z.n
2. b_{int, intError}(singletonStack;push(2);push(3);top) = λn∈Z.3
3. b_{int, intError}(singletonStack;pop;top) = λn∈Z.error

オートマトンの振る舞いと観測

Φ/Kが任意の部分固定指標として、F:Φ→Set をΦ/K上のオートマトンとします。つまり、F∈|Autom[Φ/K]| 。記号Fは、F:Φ→Set と F:C→Set の両方を表します（「プレオートマトンの定義」参照）。関手FのホムセットC(x, y)への制限をF_{x, y}と書くことにします。

オートマトンFの振る舞いbは、簡単に定義できます。

• b_{s, d} := F_{s, d}

要するに、関手Fを、SからDへのホムセットに制限したものがFの振る舞いです。オートマトンFにその振る舞いを対応させることを振る舞い観測（behavior/behaviour observation）、または単に観測（observation）と言います。

振る舞い観測は、(オートマトン ｜→ 振る舞い) という対応なので、Obs:|Autom[Φ/K]|→Beh[Φ/K] という写像になります。この定義からは、Obsは関手にはならないように思えますが、実は関手になります（後述）。

Aが伝統的オートマトンで、Fが対応する関手オートマトンだとします。このとき、Fの振る舞いは、伝統的オートマトンAが受理する形式言語と同じことです。この事実を示すことは良い練習問題です。やってみてください。

一般的関手オートマトンFをその振る舞いから調べることは、伝統的オートマトンを受理言語から調べる方法の一般化になります。伝統的マイヒル／ネロードの定理の一般化も、このラインに沿って行います。

非退化指標／非退化オートマトン

今後、振る舞い全体の集合Beh[Φ/K]を道具に使うのですが、指標グラフ Φ = (Φ, S, D) によっては振る舞いが無意味化することがあります。振る舞いbは、S×Dで添字付けられることになりますので、S×Dが空だと振る舞いは無意味になってしまいます。そこで次の条件を付けます。

• 開始頂点族Sは空ではない。
• 識別頂点族Dは空ではない。

Hid = |Φ|＼(S∪D) として、Hidが空の場合も面白くありません。次の条件も追加します。

• 隠蔽頂点族Hidは空ではない。

S, D, Hのすべてが空でない指標を非退化指標（non-degenerate signature）と呼びます。非退化指標Φを定義域とするようなオートマトン F:Φ→Set を非退化オートマトン（non-degenerate automaton）と呼ぶことにします。非退化条件を満たさないモノは、退化した指標／オートマトンです。

今後扱う指標／オートマトンは、非退化であると仮定します。退化オートマトンでは観測が出来ません。

振る舞いの反カリー化表現と観測手順

b∈Beh[Φ/K] のとき、s∈, d∈D に対して b_{s, d}:C(s, d)→Set(K(s), K(d)) ですが、少し変形しておくと取り扱いが便利になります。次の形です。

• b^∨_{s, d}:K(s)×C(s, d)→K(d)

b^∨_{s, d}は、b_{s, d}の反カリー化になっています。

集合圏SetのホムセットSet(K(s), K(d))は、集合の指数でもあるので、

• b_{s, d}:C(s, d)→K(d)^K(s) in Set

と書けます。集合圏はデカルト閉圏なので、反カリー化により指数を直積に直して、

• (b_{s, d})^∨:K(d)×C(s, d)→K(s) in Set

ここで、(-)^∨は反カリー化する演算子とします。ほんとは (-)_∨ にしたかったんですが（そのほうが辻褄が合う）、「s, d」が下付きなので「∨」は上付きにしました。

• b^∨_{s, d} := (b_{s, d})^∨

と定義して、bの反カリー化b^∨が出来上がります。

bでもb^∨でも何の変わりもありませんが、オートマトン F∈Autom[Φ/K] の振る舞いを求める行為（つまり観測）は、b^∨に基づいて次のように記述できます。

1. 開始値（開始値空間の要素） u∈F(s) を選ぶ。
2. プログラムコード（Cの射） f∈C を選ぶ。
3. 実行系F上で、uをfに適用する。
4. 評価結果（実行結果） F(f)(u)∈F(d) を見る。

このような、開始値／プログラムコードを選んでの個別観測行為をタクサンタクサン繰り返すことが、Fの観測です。観測行為の総体をObsで表すと、Obs(F)が実行系Fの振る舞いとなります。

リファクタリング補題と観測の関手性

次に述べる命題は、とても簡単に示せますが、意外な結果です。人によっては当たり前かも知れませんが、僕は驚きました。この結果を使えば、圏Autom[Φ/K]の構造を探れるな、と期待が持てたのでした。

• オートマトンの準同型写像（自然変換） α:F→G があるとき、Obs(F) = Obs(G)

Obsの定義から、s∈S, d∈D を任意に選んだとき、F_{s, d} = G_{s, d} を示せばいいわけです。αが自然変換であることから、次の図式が可換になります。

F(s) -αs→G(s)

｜         ｜

F(f)       G(f)

↓         ↓

F(d) -αd→G(d)

ところが、オートマトンはS, D上では固定化関手Kと一致するので、F(s) = G(s) = K(s), F(d) = G(d) = K(d), α_s = id_K(s), α_d = id_K(d) となり、

• F(f) = G(f)

が成立します。fは任意なので、「任意の f∈C(s, d) に対して F(f) = G(f)」が成立し、F_{s, d} = G_{s, d} が言えます。QED.

F→G または G→F のどちらか一方向でも準同型写像があれば、FとDは同じ振る舞いを持ちます。隠蔽原則の支配下にある我々に出来ることは振る舞い観測だけなので、準同型写像で結ばれた2つのオートマトンF, Gを区別することは出来ません。別な言い方をすると、準同型写像 α:F→G があるなら、振る舞いを一切変えずにインターフェイスΦ/Kの実装をFからGに（あるいはGからFに）取り替えることが出来るのです。準同型写像αはリファクタリングと捉えられます。もっと正確に言うと、準同型写像の存在がリファクタリングの正当性の保証を与えます。

Φ/Kを（一部実装付き）のインターフェイス、Φ/K-オートマトンをインターフェイスの実装、振る舞い観測は網羅的ブラックボックス・テストと解釈できます。FとGの振る舞いが一致することは、「実装FをGに取り替えても気付かれない」という意味でリスコフ置換可能性です。次のように言っていいでしょう。

• Fの振る舞いとGの振る舞いは一致する ⇔ FとGはリスコフ置換可能である

「メイヤーオートマトンに関するマイヒル／ネロードの定理を宣伝する」では次のように説明しています。

メイヤーオートマトンは、Command-Query分離されたインターフェース（メイヤー指標）の実装ですが、「アプリケーションプログラムから見て区別が付かない」とは、どんなに頑張ってテストしても挙動の食い違いを発見できない、ことです。

どんなに頑張ってテストしても挙動の食い違いを発見できないなら、それは異なる実装と考える必要はなくて、（事実はどうあれ）「同じ実装」とみなして差し支えありません。この「同じ」という概念がリスコフ置換可能性としての同値関係です。

この節の冒頭で出した「オートマトンの準同型写像（自然変換） α:F→G があるとき、Obs(F) = Obs(G)」は、「リファクタリングしても振る舞いは変わらない」と読めます。もう少し正確に言うと：

• Gを構成した。
• FからG（あるいはGからF）への準同型写像が存在する。
• このとき、GはFをリファクタリングして作った、と言ってよい。
• なぜなら、FとGは同じ振る舞いを持つから。

この点を鑑み、「オートマトンの準同型写像（自然変換） α:F→G があるとき、Obs(F) = Obs(G)」という命題をリファクタリング補題として参照します。

リファクタリング補題から、「振る舞い観測は関手と考えてよい」ことが導けます。

• α:F→G in Autom[Φ/K] に対して Obs(f) = id_Obs(F) = id_Obs(G) と定義すると、ObsはAutom[Φ/K]から離散圏とみなしたBeh[Φ/K]への関手となる。

離散圏とは、恒等射だけを射とする圏です。この関手性は、定義を知っていれば簡単に示せるのでやってみてください。

今回のまとめ

隠蔽原則とは次のことです：

• サブシステム／コンポネントの実装者は、内部構造（実装の詳細）を利用者に知らせてはならない。
• サブシステム／コンポネントの利用者は、仮に内部構造を知り得るにしても、その情報を利用してはならない。
• 我々のモデルにおいて、サブシステム／コンポネントとは一般化されたオートマトンであり、内部構造とは状態空間のことである。

隠蔽原則の支配下において可能なことは、ブラックボックス・テストだけです。テスト対象プログラムコード f∈C(s, d) と開始値 u∈K(s) を選んで実行すると、識別値 F(f)(u)∈K(d) が得られます。この行為を網羅的に行うと、K(s)×C(s, d)→K(d) が得られるますが、カリー化すれば、C(s, d)→Set(K(s), K(d)) ともみなせます。

網羅的ブラックボックス・テストの概念を抽象化すると、振る舞いの集合Beh[Φ/K]と観測関手 Obs:Autom[Φ/K]→Beh[Φ/K] として表せます。Obsが（離散圏への）関手であることは、次のリファクタリング補題から従います。

• オートマトンの準同型写像（自然変換） α:F→G があるとき、Obs(F) = Obs(G)

αの存在は実装者視点からのリファクタリングの正当性保証であり、Obs(F) = Obs(G) は利用者視点で「FとGは区別できない（リスコフ置換可能である）」ことです。