タイトルに付いている「高次圏:」の意味は、前回記事「高次圏: 用語法と文脈(主に2次元)」を参照してください。要するに、ダラダラした記事です。
「高次圏論は難しいなー」とため息をついているだけでは生産的じゃないですが、「なんで難しいか?」と考えてみるのは意味があるでしょう。難しさを引き起こす2つの要因についてダラダラ書きます。
内容:
高次化と弱化
「高次圏: 用語法と文脈(主に2次元)」で述べたように、高次圏論の用語法はハチャメチャです。これは、高次圏論を学習困難にしているひとつの理由ではありますが、問題を引き起こしているのは人間です。
人間の行為云々は抜きにしても、高次圏という対象物は、それ自体で難しい対象物です。難しさの主たる理由は複雑さでしょう。その複雑さを2種類、あるいは2方向に分けて考えるとよさそうです。
- 次元が増えることによって複雑さが増す。
- 定義を弱くすることによって複雑さが増す。
図にするとこんな(↓)感じです。
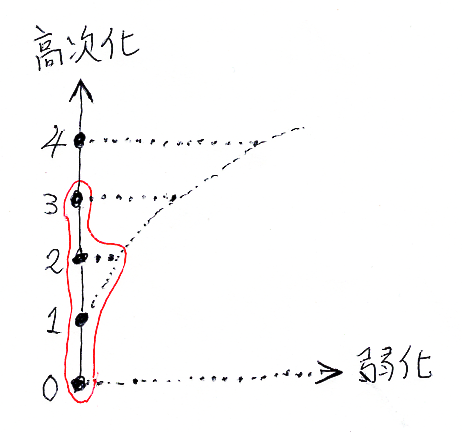
- 縦軸の0, 1, 2, 3, 4, ... は次元を表します。
- 縦軸上に乗っている黒丸は、0次元の厳密圏, 1次元の厳密圏, 2次元の厳密圏, 3次元の厳密圏, 4次元の厳密圏, ... (厳密n-圏)を表します。
- 0次元と1次元では、厳密圏しかありません。s0-Cat=集合の圏、s1-Cat=通常の圏の圏。
- 2次元以上では、厳密圏以外に弱い圏〈weak category〉が登場します。横方向は、“弱さ”の拡がりです。
- 弱さにはバリエーション(弱さの程度)があります。次元が増えるにしたがって、弱さのバリエーションは急激に増大します。
- 赤枠で囲ってある部分は、常識的な労力で定義が書き下せそうな範囲です。
最後の「常識的な労力で定義が書き下せそう」は僕の主観です。“常識的”でない例はあります。例えば、トッド・トリンブル〈Todd Trimble〉は、次元4の弱い(おそらく最も弱い)圏の定義を書き下しています。http://math.ucr.edu/home/baez/trimble/tetracategories.html の"2. The Definition of Tetracategory"から参照されているPDFに、合計51ページの定義があります。これは大変な力技で「常識的な労力」とは思えません。
弱さの集合
厳密n-圏の全体をsn-Catと書きます。sはstrictから、nは自然数を動く変数です。sn-Catの定義では、自然数nに関する数学的帰納法が使えるので、(簡単ではないが)ハッキリとした定義ができそうです。ハッキリとしていても、nが大きくなれば複雑な定義になります。
厳密とは限らない弱いn圏の全体をwn-Catと書きます。wはweakからです。任意のnに対して、wn-Catがハッキリ定義できるかどうかはよく分かりません。現状では、定義がたくさんあり、どれがベストか分かりません。そもそもベストな定義があるのかどうかも分かりません。なので、wn-Catは、実体的に存在するというより、希望的観測による想定上の存在です。
想定上の存在について語るので、雰囲気的な話になります。何もないよりは雰囲気でもあるだけマシでしょう。
いま、wn-Catは、最も弱い、あるいは完全に弱い〈fully weakened〉n-圏の定義に基づくクラス(大きい集合)だとします。すると、sn-Cat ⊆ ws-Cat と考えていいでしょう。しかし、意味のあるn-圏のクラスはsn-Catとws-Catだけに限らないでしょう。何らかの意味でのn-圏のクラスWがあり、sn-Cat ⊆ W ⊆ ws-Cat と位置付けられるでしょう。
前節の図をもう一度見てもらうと、点線の横棒は、nが多くなると幅が拡がっていきます。この横棒を“弱さ”を表すインデックス集合と考えて、Wnとします。Wnがどんな集合か? と聞かれると分かりませんが、存在はすると思います。“弱さ”を組み合わ的に分類すれば、Wnは有限集合にできる(有限種類に分類できる)のではないかと期待してます(期待だけ)。
nが何であっても、s, w∈Wn であって、任意の ρ∈Wn に対して次の包含関係が成立します。
- sn-Cat ⊆ ρn-Cat ⊆ ws-Cat
ρ, τ∈Wn に対して、
- ρn-Cat ⊆ τs-Cat ⇔ ρ ≦ τ
となるような順序関係≦を定義できます(できると想定する)。この順序関係で、sは最小元、wは最大元です。
nが2, 3, 4くらい(低次元のケース)なら、Wnとその上の順序構造を具体的に決定できるんじゃないのかな(期待だけ)。Wnがハッキリすれば、それはn-圏の世界の地図のようなものになります。
半厳密n-圏
半厳密n-圏〈semistrict n-category〉という概念があります。各次元ごとのWnと、ρ∈Wn に対するρn-Catが定義されて、さらに弱n-圏の同値性が定義されれば、半厳密性も定義できます。ここで、弱n-圏の同値性とは、「弱n-圏として事実上同じ」ことですが、nが大きくなれば同値性の定義も大変になります。n = 2, 3 のケースでは、biequivalent, triequivalentとして同値性が定義されています。
ρ∈Wnに対するρn-Catが次の性質を持つとします。
- 任意の C∈|wn-Cat| に対して、CとDが同値となる D∈|ρn-Cat| が存在する。
最も一般的なクラスwn-Catの代わりにρn-Catを用いても大丈夫だ、ということです。
ρn-Catが上の性質を持っていて、さらに次が成立するとします。
- τ < ρである任意のτ(τ∈Wn)に対して、τn-Catは上の性質を持たない。
つまり、ρを小さくするともはや一般性を失います。一般性を失わないで、ギリギリまで厳密方向に近いn-圏達のクラスがρn-Catです。このとき、ρn-Catの対象を半厳密n圏と呼びます。Wnが全順序とは限らないので、半厳密n-圏の定義も一意的ではありません。
n = 2 では、すべての弱2-圏が厳密2-圏と同値(biequivalent)なので、半厳密性は n ≧ 3 で意味を持ちます。n = 3 では、Gray-圏の圏が半厳密性を持つことが知られています。
半厳密性を持つ ρ∈Wn が見つかれば、ρn-Cat は“n-圏の圏”としての一般性を持ち、厳密に近いことから扱いやすいはずです。半厳密n-圏のクラスを見つけることは、適切な作業環境を手に入れることなので重要です。wn-Catではなくても、何らかの目的に対して十分なτn-Catがあるとき、τn-Catに対する“半厳密n-圏の圏”ρn-Catも役に立ちます。