小さい圏Cから集合圏Setへの関手 F:C→Set に限定して、その極限を具体的に扱います。具体的とは、極限を、(無限かも知れない)直積と条件絞り込みで実際に構成することを意味します。具体的構成の方針(精神)は、「錐〈すい〉集合関手の表現対象を作りましょう」です。
内容:
- 具体的に具体的に
- 関手の極限の復習
- 錐集合関手と関手の表現対象
- 錐の圏の終対象と錐集合関手の表現対象
- プレ錐集合の表現集合
- “頂点Xのプレ錐”と“Xから直積への写像”
- 錐条件で絞り込む
- 例:スパンの極限
- おわりに
具体的に具体的に
圏論における極限(とその双対である余極限)は重要な概念ですが、最初は実感が湧きにくいかも知れません。そこで、状況設定を限定する(一般性を犠牲にする)ことで、極限を手で触れる(感じがする)モノとして定義します。限定した状況設定を以下に述べます。
Cは、この記事を通じて小さな圏とします。Cの対象は、i, j, kなどの小文字で表すことにします。そのココロは、Cの対象を単なるインデックス(ラベル、番号、名前)として扱おう、ということです。圏の対象を集合だと思いこんでいる人、あるいは対象=集合のイメージが捨てられない人は多いみたいですが、Cの対象は単なるインデックスだと思ってください。なんなら、|C|⊆N と考えてください -- このとき、Cの対象は自然数です。
Cとして使いそうな具体例をいくつか挙げます。これらの例では、|C|⊆N と考えることができます。
- 空圏〈{empty | null} category〉: 対象も射もひとつもない圏です。“圏の圏”の始対象なので、始圏〈initial category〉と呼ぶこともあります。
- 一点離散圏〈one-{point | object} discrete category〉: 対象がひとつと、その恒等射だけからなる圏です。終圏〈{final | terminal} category〉、自明圏〈trivial category〉、単位圏〈unit category〉と呼ぶこともあります。
- ニ点離散圏〈two-{point | object} discrete category〉: 対象がふたつと、それぞれの恒等射だけからなる圏です。2と書かれることがあります。
- アロー圏〈arrow category〉: 対象がふたつと、それぞれの恒等射、一本の非恒等射だけからなる圏です。これも2と書かれることがあります -- '2'が二点離散圏かアロー圏かを確認する必要がありますね。二値ブール集合の論理的順序(false < true)から得られる圏はアロー圏です。アロー圏{・→・}から圏Dへの関手圏[{・→・}, D]を、(Dの)アロー圏(category of arrows)と呼ぶこともあるので注意してください。あと、ヒューズ(John Hughes)のアローってのもあります。曖昧さを避けるには単アロー圏〈{one- | single-} arrow category〉と呼ぶのが安全かも知れません。
- 離散圏〈discrete category〉: 集合Sを圏とみなしたものです。対象はSの要素、射は恒等射しかありません。S = {}, {0}, {1, 2} のとき、対応する離散圏はそれぞれ、空圏、一点離散圏、二点離散圏です。
- 余離散圏〈codiscrete cateory〉: 集合Sを頂点集合とする有向完全グラフを作って、それを圏とみなしたものです。射の集合Mor(C)は、S×Sと1:1対応します。密着圏〈indiscrete category〉、カオス圏〈chaotic category〉とも呼びます。
- 平行対〈parallel pair〉: 対象がふたつ、恒等射、同じ向きのニ本の非恒等射だけからなる圏です。
- スパン〈span〉: 対象が3つで、二本の非恒等射が ・←・→・ の形をした圏です。
- {余 | コ}スパン〈cospan〉: 対象が3つで、二本の非恒等射が ・→・←・ の形をした圏です。
- 有限箙からの自由圏: Qを有限個の頂点と有限本の辺を持つ箙〈えびら | quiver〉(多重辺と自己ループ辺を許す有向グラフ)として、Qから生成される自由圏とは、Qの道(繋がった辺の列、パス)を射とする圏です。「圏論番外:有向グラフのパスの圏(実装付き)」参照。
- 片側無限系列: 自然数Nの普通の順序構造 0<1<2< ... から作った圏です。
これはいずれも可愛い圏です。形式的には、Cは小さい圏であれば何でもいいですが、可愛い圏*1で考えると具体性が増すと思います。
これから考える関手は、上記のような小さい圏Cからの関手に限ります。関手が値をとる圏は集合圏Setです。Setは大きな圏ですが、お馴染みの圏ですね。関手 F:C→Set は、Cの対象や射でラベルされた図式〈diagram〉と考えられます。その図式は集合圏内にあるので、頂点は集合、矢印は写像です。関手Fを“集合と写像からなる図式”と考えたとき、圏Cは図式の形状〈shape〉を与えます。
この節のタイトルに「具体的に」が二回繰り返されてますが、4回繰り返しの話が次の記事にあります。具体例を知らないと妄想的な思弁に奔〈はし〉る危険があるので、具体的に、具体的に、…
関手の極限の復習
関手の極限の話はあんまり書いてないなー、と思ったんですが、2012年の記事がありました。
この過去記事に説明と定義があります。現時点(2018年)でも同じ説明しか思いつかないので、極限の導入と定義は上記記事を見てください。記号・用語も上記記事にほぼ従います。次の用語はそのまま使います。
- 錐〈cone〉
- 頂点〈apex〉
- 底面〈base〉
- 錐の圏〈category of cones〉
錐の「母線」〈generating line〉という言葉はやめます(下図)。「母線」の図形的な意味は、下図の意図と違いますから。
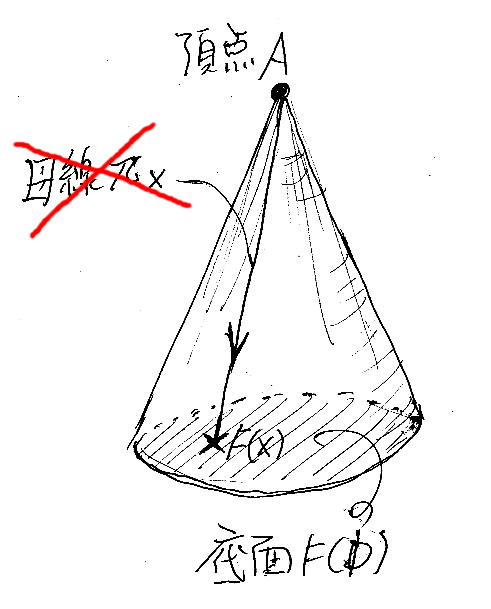
頂点と底面の点を結ぶ線は、錐を自然変換と考えたときの成分〈component〉に相当するので、成分線〈component {segment | arrow | line}〉にします*2。
関手 F:C→Set に対して、底面Fの錐の圏はCone(F:C→Set)、または単にCone(F)と書きます(2012年記事と同じ)。Cone(F)をConeFと書くときもあります。例えば、圏Cone(F)のホムセットは、Cone(F)(α, β) より ConeF(α, β) のほうが見やすいでしょう。
底面がFで頂点がAである錐の集合をCone(F)[A]と書くのは、錐の圏と紛らわしいので、ConeSetF(A)に変えます。ConeSetは圏ではなくて錐集合〈set of cones〉です。ConeSetF = |ConeF| 。Aを引数と考えた A|→ConeSetF(A) は Set→Set という関手になります(次節で詳述)。
「関手Fの極限」といったときに、その意味が曖昧だったり誤解しがちだったりするので、ここでハッキリさせておきましょう。まず、同義語がたくさんあります。
| 最近の用語 | 極限〈limit〉 | 余極限〈colimit〉 |
|---|---|---|
| 古めの用語 | 逆極限〈inverse limit〉 | 順極限〈直極限 | direct limit〉 |
| 別な用語 | 射影極限〈projective limit〉 | 帰納極限〈inductive limit〉 |
「順極限=極限、逆極限=余極限」ではないので注意してください。ときに逆極限と呼ばれるものが圏論的な極限です。表の縦の欄は同義語なので区別する必要はありません。
[追記]マックレーンの教科書(The Book)の第III章を見たら、極限は左根〈left root〉とも呼ぶと書いてありました(幸いに、今では死語に近いでしょうが)。一方、右カン拡張は極限の一般化です。双対も含めて同義語・類義語を並べると:
- 極限=逆極限=左根≒右カン拡張
- 余極限=順極限=右根≒左カン拡張
圏論用語のむちゃくちゃ・ハチャメチャぶりがよく分かる事例ですね。[/追記]
Fの極限はFを底面とする錐の圏Cone(F)の終対象(余極限は余錐の圏の始対象)として定義されます。この定義を文字通りに受け取ると、極限とは錐です。しかし多くの場合は、極限とは対象を意味するでしょう。この2つが区別されないことが多いですが、ここでは区別しましょう。
- LimCone(F)は、Fの極限錐〈limiting cone〉を意味する。Fの極限錐は、錐の圏Cone(F)の終対象である。LimCone(F)∈|Cone(F)|
- LimObj(F)は、Fの極限対象〈limit object〉を意味する。Fの極限対象は、Fの極限錐の頂点である。LimObj(F)∈|Set|(一般には、LimObj(F)はFの余域である圏の対象)
こう定義した上で、Limまたはlimは文脈で解釈してください、となります。実際の使用例を見ると、文脈なしでは判断できないようです。
錐は特殊な自然変換とみなせるので、α, βなどのギリシャ文字小文字で表すことにします。頂点がAで底面がFである錐は α::A⇒C F:C→Set と書くことにします。自然変換の書き方とほとんど同じです。区別するために、プレーンな'⇒'ではなくて'⇒C'としています。下付きのCはconeの'C'です。錐αに対して、apex(α) := A、base(α) = F で頂点と底面を取り出すことにしましょう。一般の自然変換と錐の用語・記号の対応を表にまとめます。
| 自然変換 α::G⇒F | 錐 α::A⇒C F |
|---|---|
| αの域 dom(α) = G | αの頂点 apex(α) = A |
| αの余域 cod(α) = F | αの底面 base(α) = F |
| Fのiでの値 F(i) | 底面の点 F(i) |
| αの成分 αx:G(i)→F(i) | αの成分 αi:A→F(i) |
| 自然性条件 | 錐条件 |
最後の錐条件〈cone condition〉とは次の等式です。底面内の射と2本の成分線が作る三角形の可換性を主張しています。
- すべての φ:i→j in C に対して、αi;F(φ) = αj
「具体的に、具体的に」のモットーに基づけば、具体的な小さな圏Cに対して、具体的な関手 F:C→Set を与えて、具体的に錐の圏Cone(F)を構成して、その終対象として極限錐を求め、極限錐の頂点として極限対象を取り出してみるべきです。幾つかやってみます。
- Cが空圏のとき、関手 F:空圏→Set はただ1つ在り、唯一のFに対して Cone(F) = Set です。したがって、LimObj(F)はSetの終対象〈{final | terminal} object〉です。
- Cが一点離散圏のとき、F:{0}→Set は F(0)∈|Set| で決まるので、F(0) = A とすると、頂点Xの錐は X→A という写像で、Cone(F) = Set/A です。ここで、Set/Aはアンダー圏で、LimObj(F)はAです。
- Cがニ点離散圏のとき、F:{1, 2}→Set は F(1), F(2)∈|Set| で決まるので、F(1) = A, F(2) = B とすると、頂点Xの錐は X→A, X→B という写像の対で、Cone(F) = SPANSet(A, B) です。ここで、SPANSetは、「スパンの圏と行列の圏」で定義しているSPAN(Set)と同じです。LimObj(F)は直積〈direct product〉A×Bです。
- Cが平行対のとき、F:平行対→Set は、両端(始域と終域)を共有する2つの写像 f, g:A→B です。集合Xを頂点とする錐は、e;f = e;g を満たすような e:X→A を成分として、残りの成分は e;f, e;g で与えられます。LimObj(F)はfとgの等値核〈イコライザー | equalizer〉です。
錐は自然変換に似てるのではなくて、自然変換そのものです。集合Aを選んで、関手 G:C→Set を次のように定義します。
- G(i) = A
- G(φ:i→j) = (idA:A→A)
GからFへの自然変換を α::G⇒F:C→Set とすると、αは、Aを頂点としてFを底面とする錐と同じものです。錐条件は、自然変換の自然性条件です。錐と一般の自然変換で用語・記法を区別しないというやり方もあるでしょうが、ここでは錐特有の用語・記法を導入しています。
錐は特殊な自然変換なので、自然変換の一般論はすべて適用できます。例えば、“関手の極限対象を取る操作LimObj”は、“対象から定数関手(Gのような関手)を作る操作Const”の右随伴として定義できます。
- SetC(Const(X), F)
Set(X, LimObj(F))
- Const -| LimObj :SetC→Set
同様に、
- Set(ColimObj(F), Y)
SetC(F, Const(Y))
- ColimObj -| Const :Set→SetC
一緒にすると随伴トリオ(「カン拡張における上下左右: 入門の前に整理すべきこと // 随伴トリオとその例」参照)になります。
- ColimObj -| Const -| LimObj
「カン拡張における上下左右: 入門の前に整理すべきこと // 随伴トリオとその例」で述べた Σ -| Δ -| Π は、ColimObj -| Const -| LimObj の特殊例(C = (n点離散圏))です。
[/補足]
錐集合関手と関手の表現対象
関手(図式) F:C→Set を固定して、集合X(X∈|Set|)を選びます。底面がFでXを頂点とする錐の全体をConeSetF(X)とします。
- α∈ConeSetF(X) ⇔ αは、底面がFでXを頂点とする錐
Fは固定したままで集合Xを動かすと、X|→ConeSetF(X) は |Set|→|Set| という対応になります。写像 f:X→Y に対して、f*:ConeSetF(Y)→ConeSetF(X) を次のように定義できます。
- すべての i∈|C| に対して、(f*(β))i := f;βi
このように定義されたf*(β)が、実際に“底面がFでXを頂点とする錐”になることは確認が必要です(練習問題)。f*が写像 ConeSetF(Y)→ConeSetF(X) としてちゃんと定義されている〈well-defined〉であると分かったら、ConeSetF(f) := f* とします。これにより、ConeSetF(-):Setop→Set は(反変の*3)関手となります(これも確認必要)。
関手 F:C→Set に対して、ConeSetF:Setop→Set という関手が作れることが分かりました(2012年記事では、ConeSetFをf^と書いています)。集合Xに錐集合を対応させる関手ConeSetFを(底面がFの)錐集合関手〈cone-set functor〉と呼びましょう。
ここで、表現可能関手〈representable functor〉と表現対象〈representing object〉をちょっとだけ復習します。Dを必ずしも小さくない圏として、関手 K:Dop→Set (Dから集合圏への反変関手)を考えます。Dの対象rがあって、反変関手Kが反変ホム関手D(-, r)と同値になる*4とき、次の言い方をします。
- K:Dop→Set は表現可能〈representable〉な関手である。
- Dの対象rは、関手 K:Dop→Set を表現〈represent〉する
- Dの対象rは、関手 K:Dop→Set の表現対象〈representing object〉である。
例えば、反変ベキ集合関手Pow:Setop→Set に対して、次が成立するので、{0, 1}が反変ベキ集合関手の表現対象です。
- ∀X∈|Set|. Pow(X)
Set(X, {0, 1})
- ∀f:X→Y in Set. Pow(f:X→Y)
Set(f, {0, 1})
今回の例では、反変関手ConeSetFが注目している関手です。ConeSetFの表現対象(があるとしてそれ)をRと置きましょう。表現対象の定義から、
- ∀X∈|Set|. ConeSetF(X)
Set(X, R)
- ∀f:X→Y in Set. ConeSetF(f:X→Y)
Set(f, R)
PowもConeSetFも、SetからSetへの反変関手なので、表現対象があればそれは集合ですから、集合値反変関手の表現集合〈representing set〉と呼んでもいいでしょう。
錐の圏の終対象と錐集合関手の表現対象
この記事の目的は、錐集合関手 ConeSetF:Set→Set の表現対象(表現集合)Rを具体的に構成することです。では、何のために構成するのか、構成して何がうれしいのか? それを確認しておきます。
次の事実があります。
- 錐集合関手の表現対象があれば、それは同型を除いて一意的である。
- 錐集合関手の表現対象があれば、それから錐の圏の終対象を構成できる。
- 錐の圏の終対象があれば、それから錐集合関手の表現対象を構成できる。
- 上記の構成は互いに逆で、1:1の対応を与える。
これらのことから、錐集合関手の表現対象(表現集合)を作ってしまえば、それはもとの関手 F:C→Set の極限(錐の圏の終対象)になるわけです。作り方がどうであれ、でき上がるものは同型なので、作り方は気にせずに(できりゃいいのだ)、とにかく頑張ればいいのです。表現対象を作れば、極限対象が手に入るのです。
さて、上記の事実の2,3,4番は、錐集合(錐集合関手の値)と写像の集合(ホムセット関手の値)の系統的1:1対応から、「錐の圏の終対象」と「錐集合関手の表現対象」が同じ概念になると主張しています。そうなると、終対象の(up-to-isoでの)一意性から、表現対象の一意性(1番の事実)も出てきます。この流れだと1番は余分な前提といえます。
2,3,4番の事実は、カン拡張の立場から解釈するのがよさそうなので、今日は「そんな背景があるよ」で済ませます。余分な前提に見える1番「関手の表現対象があれば、同型を除いて(up-to-isoで)一意的」は、2,3,4番とは独立な一般論から言えるので、以下に述べます。(オマケなので飛ばしてもいいです。)
ConeSetFに限らず、一般的な枠組みで語ります: Dは(必ずしも小さくない)圏だとして、K:Dop→Set を関手とします。r∈|D|を関手Kの表現対象だとします。つまり、
- K(x)
D(x, r) in Set
ここで、xはDの対象全体を走ります。
- ∀x∈|D|.( K(x)
D(x, r) in Set )
しかも、対象xごとに与えられる“集合の同型”は、xごとにパランパランにあるわけではなくて、系統的に連携しています。これはつまり、関手Kと関手D(-, r)のあいだに自然同型(可逆な自然変換で与えられる同型)がある、ということです。
関手圏[Dop, Set](D上の前層の圏ともいう)で考えましょう。関手圏の対象KとD(-, r)は、関手圏内で同型なので、
- K
D(-, r) in [Dop, Set]
同型の右辺D(-, r)は、米田埋め込み〈Yoneda embedding〉による r∈D の像です。「米田の「よ」とか: ちょっと変わった記法・名前達」と「困った時の米田頼み、ご利益ツールズ」の記法で書くなら:
- D(-, r) = λx.D(x, r) = よ(r) = r米
いま、Fの表現対象をもうひとつ取ってきてsとします。rもsも表現対象であることから、
- K
r米 in [Dop, Set]
- K
s米 in [Dop, Set]
したがって、
- r米
s米 in [Dop, Set]
ここで、米田埋め込みの性質を思い出しましょう(例えば https://ncatlab.org/nlab/show/Yoneda+embedding 参照)。米田埋め込み よ = (-)米 は、D→[Dop, Set] という充満忠実関手〈full-and-faithful functor〉です。Dは、[Dop, Set]のなかに、充満部分圏〈full subcategory〉としてそのままスッポリ入り込んでいるのです(だから「埋め込み」と呼ぶ)。
以上のことにより、埋め込み先における同型 r米 s米 から、もとの圏Dにおける同型 r
s が導けます。そう、関手Kに対する2つの表現対象rとsは同型です。
プレ錐集合の表現集合
いきなり錐集合関手の表現集合を作るのではなくて、準備としてプレ錐集合関手(すぐ後に説明)の表現集合を構成します。関手 F:C→Set はずっと固定したままです。
集合Xに対して、Xを頂点としてFを底面とするプレ錐〈precone〉とは、i∈|C| ごとに、写像 αi:X→F(i) を割り当てた族とします。錐とは違い、錐条件はありません。
プレ錐αとは、|C| = Obj(C) をインデックス集合〈indexing set〉とする写像の族 α:Obj(C)→Mor(Set) で次の条件を満たすものです。
- dom(αi) = X
- cod(αi) = F(i)
Xを頂点としてFを底面とするプレ錐の全体をPreconeSetF(X)と書きます。
- PreconeSetF(X) = {α:Obj(C)→Mor(Set) | ∀i∈Obj(C).(dom(αi) = X) ∧ ∀i∈Obj(C).(cod(αi) = F(i)) }
プレ錐では錐条件がないということは、φ:i→j in C があっても、φが考慮されないことです。Cが離散圏のときのプレ錐は錐になります(もともと非恒等な射φがないので)。こういう言い方もできます: 関手 F:C→Set の対象部〈object part〉 Fobj:Obj(C)→Obj(Set) だけでプレ錐は決定される。
錐の場合と同様に、PreconeSetF(-)を集合圏Setの自己反変関手にできます。
- PreconeSetF:Setop→Set
集合Qがプレ錐集合関手の表現集合であるとは、次の同型が成立することです。
- PreconeSetF(X)
Set(X, Q)
多少の後知恵を使うと: Cが離散圏のときのプレ錐は錐でもあるので、集合Qは離散圏からの関手の極限となり、QはF(i)達の直積だと見当が付きます(あくまで後知恵だけど)。
実際、QはF(i)達の直積となり、次の同型が成立します。
- PreconeSetF(X)
Set(X, Π(F))
Π(F)という簡略な記法を使いましたが、丁寧に書けば次のようです。
「写像、集合族、直積」という集合に関する基本概念を使えば、上記の同型は“明らか”と言えなくもありませんが、“明らかとは思えない”人もいると思います。次節で“具体的に”追いかけてみます。
“頂点Xのプレ錐”と“Xから直積への写像”
F:C→Set は相変わらず固定しています。プレ錐の話のときは、Cの射は何の役割も演じないので、Cを集合(離散圏)と思ってもかまいません。この設定では、関手Fは、|C| = Obj(C) をインデックス集合とする集合族に他なりません。集合族、集合の直和、集合の直積に関しては、「集合族と集合の集合、関連する構成法」の最後の2つの節を読んでください。
集合X, Yに対して、Set(X, Y), YX, Map(X, Y) という記法を使いますが、これらはすべて同じ意味です。しかし、使う場面により次のニュアンスがあります。
- Set(X, Y)は、集合圏Setを外から眺めたときの(外部)ホムセット。Set(X, Y)⊆Mor(Set) と捉える。
- YXは、2つの集合X, Yから作った指数対象(ベキ対象)。YXの要素は、eval:YX×X→Y により関数として機能するが、YXは単なる集合に過ぎない。YX∈|Set| と捉える。
- Map(X, Y)は、集合圏Setは意識せずに、集合のあいだの写像の集合を表したもの。必要に応じて、Map(X, Y) = Set(X, Y)、Map(X, Y) = YX と解釈するかも知れない。
(i∈I |→ F(i))が集合族のとき、∪(F), Σ(F), Π(F)を次のように定義します。
最後のSectについては「集合族と集合の集合、関連する構成法 // 直和のセクションの集合=直積」を見てください。この記事では、直積をセクションの集合として定義します。
集合族(i∈I |→ F(i))に対して、直積Π(F)が上記のように定義できますが、i∈I に対するi番射影〈i-th projection〉πiは次の通りです。
- y∈Π(F) に対して、πi(x) = y(i)
射影πiは、iによる球値写像です。
ここまで準備をすれば、PreconeSetF(X) Set(X, Π(F)) が自明に見え始めると思います。
α∈PreconeSetF(X) を取ると、これは i∈|C| ごとに αi:X→F(i) という写像を割り当てます。x∈X をαiに渡すと:
- αi(x)
これを、
- αi(x) = α'(x)i
と書き換えてみます。α'は、xを引数にもらって直積Π(F)に値を持つ関数です。
- α':X→Π(F) where α'(x)i = αi(x)
α |→ α' という対応が、PreconeSetF(X)→Set(X, Π(F)) の方向の写像です。逆方向の対応も同様に作れて、α←→α' は同型となります。
もう少しハッキリと言えば、次のような定義/同型があるのです。(iは、|C| = Obj(C) の上を走る変数とします。)
- セクション集合の定義
- 直積集合の定義
- 積と指数に関する分配法則
1. セクション集合の定義
一番上の等式は、集合族のセクション集合の定義です。考える族は、(i |→ F(i)X)です。F(i)は関手(の対象部)として与えられています。Xは決まった集合なので、指数集合F(i)Xもiに依存して変わる集合族です。その集合族のセクション集合は、イコールの右辺のように定義されます。
αは写像ですが、α(i)の代わりにαiと書いています。写像αがセクションであるとは、値αiが、“X→F(i) という写像”、つまり指数集合(関数集合)F(i)Xの要素である必要があります -- という条件によりセクション/セクション集合が定義されます。
セクションの定義は、XからFへのプレ錐の定義と同じなので、セクション集合プレ錐集合 です。セクション集合=プレ錐集合 だと思ってもいいです。
2. 直積集合の定義
族(i |→ F(i)X)の直積をセクションとして定義しています。ここでは、セクション集合と直積集合、セクションとタプル、球値と射影は同義語です。
3. 積と指数に関する分配法則
この同型に名前がないようですが、表題のように呼べばいいかと。普通の分配法則は和と積に関するものですが、それを積と指数(ベキ)にした形をしていますから。
,
で、αとα'が対応しているとき、次が成立しています。
- (πi(α))(x) = πi(α'(x))
あるいはもっと簡略に:
- αi(x) = α'(x)i
要するに、αはi(i∈|C|)とx(x∈X)に依存して値が変化するのですが、iとxのどちらを先に考えるかの順序を変えているだけです。iが先に変化すると思えば、プレ錐=関数値のセクション=関数成分を持つタプルで、xが先に変化すると思えば、直積への関数です。
錐条件で絞り込む
前節で、プレ錐の集合PreconeSetF(X)とホムセットSet(X, Π(F))の同型を構成しました。次のような同型や等式から言えました。
- プレ錐集合はセクション集合と同型(または同じ)
- セクション集合と直積集合は同じ
- 積と指数に関する分配法則
- 直積集合の略記
- 集合の指数とホムセットは同じ
PreconeSetF(X)は錐条件を考えてないので、錐として認められないプレ錐が混じっています。それら不適切なプレ錐をふるい落とせば錐の集合が得られます。つまり、錐集合ConeSetF(X)はプレ錐集合PreconeSetF(X)の部分集合になり、次のように書けるはずです。
- ConeSetF(X) = {α∈PreconeSetF(X) | αの錐条件 }
錐条件は、射 φ:i→j in C ごとに、写像の三角形「F(φ), αi, αj」に関する可換性を書けばいいので、次の論理式になります。
- ∀φ:i→j in C. αi;F(φ) = αj
あるいは次の形にも書けます。
- ∀φ∈Mor(C). αdom(φ);F(φ) = αcod(φ)
この条件を、Π(F)上の条件に翻訳すれば、錐集合関手の表現集合 R⊆Π(F) が得られます。
とりあえず、αi;F(φ) = αj のイコールが関数の等値なので、変数xを入れて書き換えます。
- ∀x∈X. F(φ)(αi(x)) = αj(x)
αi(x) = α'(x)i、αj(x) = α(x)j を使ってα'に関する条件にすれば、それはΠ(F)上の条件になります。
- ∀x∈X. F(φ)(α'(x)i) = α'(x)j
y∈Π(F) に関する条件として書けば:
- F(φ)(yi) = yj
さらに、Π(F)の部分集合Rの定義に書きかえましょう。
- R = {y∈Π(F) | ∀φ:i→j in C. F(φ)(yi) = yj}
集合Xから、Π(F)の部分集合Rへの写像 f:X→R があれば、fから αi(x) := πi(f(x)) として構成した(i∈Obj(C) |→ αi)は錐条件を満たします。細部を確認すれば、次の同型(Xに関して“自然”な同型)が得られます。
- ConeSetF(X)
Set(X, R)
例:スパンの極限
Cがスパンの場合に極限=錐集合関手の表現対象を求めてみます。Cは次の通りとします。
- |C| = {1, 2, 3}
- Mor(C) = {a:1→3, b:2→3, 恒等射達}
F:C→Set は次の通り:
- F(1) = A (Aは集合)
- F(2) = B (Bは集合)
- F(3) = C (Cは集合)
- F(a) = f:A→C (fは写像)
- F(b) = g:B→C (gは写像)
Π(F)はA×B×Cであり、表現対象(表現集合)Rは、次のように与えられます。
- R = {y∈A×B×C | ∀φ:i→j in C. F(φ)(yi) = yj}
∀φ:i→j を5つの射それぞれに展開すると:
- F(id1)(y1) = y1
- F(id2)(y2) = y2
- F(id3)(y3) = y3
- F(a)(y1) = y3
- F(b)(y2) = y3
恒等に関する条件は常に真なので、a, b∈Mor(C) に関する条件だけが効いて:
- F(a)(y1) = f(y1) = y3
- F(b)(y2) = g(y2) = y3
Rの定義は次のように書き直せます。
- R = {(y1, y2, y3)∈A×B×C | f(y1) = y3 ∧ f(y2) = y3}
あるいは、
- R = {(a, b, c)∈A×B×C | f(a) = c ∧ f(b) = c}
通常、スパンの極限として“AとBのファイバー積”を取りますが、Rは“AとBのファイバー積”と同型です。
おわりに
小さい圏Cからの関手 F:C→Set に関しては、極限に関する具体的な表示が得られました。
- LimObj(F) = {y∈Π(F) | ∀φ:i→j in C. F(φ)(yi) = yj}
これを使えば、極限は必ず求まります。冒頭に挙げた小さい圏達に適用してみてください。
次の3つのことは保留になっています。
- 錐集合集合の表現対象と、錐の圏の終対象が同じであること。
- ConeSetF(X)
Set(X, R) が自然同型であること。
- プレ錐集合を絞り込む条件=錐条件が、2つの写像の等値性として書けること。
これらはまた別な機会に。