ド・ラーム・コホモロジーとホッジ分解のオモチャ (1/2)

技術者・プログラマが、ド・ラーム理論〈de Rham theory〉やホッジ理論〈Hodge theory〉を必要とすることなんてあるのか？ ほとんどないとは思うのですが、「稀にはある」というのはどうも事実のようです。

なので、そのテの話をします。簡単なオモチャ〈toy model〉に関して、ド・ラーム・コホモロジーと調和形式によるその表示を、線形代数の技法だけで定式化します。その際、多様体や微積分の知識は仮定しませんし、使いもしません。ただし、背景や周辺のオハナシではいろんな概念が登場します、オハナシとして。

今回・前編(1/2)と次回・後編(2/2)の2回に分けて書きます。「ド・ラーム・コホモロジーとホッジ分解のオモチャ」の中核となる有限次元線形代数の議論は次回に行います。今回は、全体像や周辺知識、準備的な項目についてウダウダ述べます。

内容：

次回・後編の内容：

1. この記事の記述方法について
2. 内積ベクトル空間と随伴線形写像
3. 部分空間の直交性と直交補空間
4. ホッジの分解定理（ラプラシアンなしバージョン）
5. ラプラシアンとホッジ分解
6. ド・ラーム・コホモロジー空間
7. 多様体から線形代数へ
8. おわりに

予備知識は線形代数だけ

ド・ラーム理論はなめらかな多様体、ホッジ理論はさらにリーマン計量を持つ多様体上で展開される理論です。したがって、本質的に微積分に依存しています。それにも関わらず、できるだけ組み合わせ的／代数的に定式化すれば、多様体にも微積分にも依存しない構造を取り出すことが出来ます。

こうして取り出した構造（有限離散近似）では、接ベクトルや計量のような大事な概念が欠落してますが、取り扱いがとても簡単なので、オモチャとしてイジるには適しています。そんなオモチャでも、雰囲気を感じ取るにはまーまー役立ったりします。

というわけで、オモチャの話をします。オモチャの構成に位相空間や多様体の知識は全く不要ですし、微積分も使いません（背景を理解するとなると話は別ですが）。しかし、線形代数はそれなりに使います。次の言葉は理解している必要があります。

1. ベクトル空間〈線形空間〉
2. ベクトル空間の基底
3. 集合から作る自由ベクトル空間
4. 線形写像
5. 双対ベクトル空間と双対線形写像
6. 線形写像の核空間
7. 線形写像の像空間
8. ベクトル空間の部分空間による商空間
9. 線形写像の準同型定理 V/Ker(f) Im(f) where f:V→W
10. 内積ベクトル空間と随伴線形写像（次回の記事内で説明あり）

オモチャとして出てくるベクトル空間はすべて有限次元です。有限次元の線形代数を使って、（次回だけど）ド・ラーム理論とホッジ理論のミニチュアを組み立てます。

• お急ぎの方は次回へどうぞ。

背景のオハナシ（超・急ぎ足）

ド・ラーム・コホモロジーとホッジ分解のオモチャの構成には、ほんとに線形代数しか使わないので、純粋に代数的な話として理解することもできます。しかし、それでは味気ないという方のために、背景の説明をたいへんな急ぎ足でします。この節は、後（主に次回）で出てくる記号や用語が唐突過ぎるという感じを幾分かはやわらげるのに役立つでしょう。「この節がサッパリわからん」だとしても、次節以降（次回も含む）を読むのに差し支えはありません。なんなら、スキップしてもかまいません。

扱いやすくタチの良い図形を多様体〈manifold〉と呼びます。多様体の次元〈dimension〉とは、僕らが直感的に“図形の次元”と理解している“あの次元”のことです。Mをn次元の多様体とします。Mの図形的性質が反映された代数的情報をMから取り出したい、としましょう。そんな情報のひとつに、Mのコホモロジーがあります。スカラーとして実数を使うと決めれば、Mのコホモロジーは、実数係数ベクトル空間の添字族〈indexed family〉になります。

Mのコホモロジー H⁰(M), H¹(M), H²(M), ... （上付き添字は番号／インデックスで、各H^k(M)は実数係数ベクトル空間）を定義するひとつの方法として、M上の実数値関数の全体Ω⁰(M)を利用する方法があります。M上で微積分（ベクトル解析）ができるなら、関数 f∈Ω⁰(M) は微分できるので、関数fの微分dfが定義できます（ベクトル解析をご存知の方は、だいたい df = grad(f) と思ってください）。ここで、dfはもはやΩ⁰(M)の要素ではなくて、関数とは別なナニモノカの集合Ω¹(M)に属します。つまり、d:Ω⁰(M)→Ω¹(M) です。Ω¹(M)の要素は、関数の微分（無限小変位）を表すものなので、微分形式〈differential form〉と呼びます。

微分作用素（正確には外微分作用素〈exterior derivative operator〉）dは、d = d⁰ :Ω⁰(M)→Ω¹(M) だけではなく、d¹:Ω¹(M)→Ω²(M), d²:Ω²(M)→Ω³(M), ... のような系列として定義できます。各Ω^k(M)は（実数係数の）ベクトル空間で、その要素はk次の微分形式〈differential form of degree k〉、あるいはより短くk-形式〈k-form〉と呼びます。各d^kは線形写像で、k次の外微分作用素〈exterior derivative operator of degree k〉です。また、d^k+1d^k = 0 を満たします（これ重要！）。記号''は作用素（線形写像）の反図式順の結合記号〈anti-diagrammatic composition symbol〉です*1。

(... → Ω^-1(M) - d^-1 → Ω⁰(M) - d⁰ → Ω¹(M) - d¹ → Ω²(M) - d² → ...) という、ベクトル空間Ω^k(Ω)達と線形写像d^k達の無限系列を、Mのド・ラーム複体〈de Rham complex〉と呼びます。ここで、kが負整数のときのΩ^k(M)はゼロ空間です。k ＞ n のときのΩ^k(M)もゼロ空間になります。無限系列とはいっても、非ゼロな部分は有限個しかありません。

H^k(M) := Ker(d_k)/Im(d_k-1) と定義して作ったベクトル空間の族 (..., H^-1(M), H⁰(M), H¹(M), H²(M), ...) が、Mのド・ラーム・コホモロジー〈de Rham cohomolgy〉です。H^k(M)には、M上のk-形式の振る舞いの情報がエンコードされています。ひいてはそれが、Mの図形的性質も反映します。

ド・ラーム複体を構成するk-形式のベクトル空間Ω^k(M)達に内積が入ったとしましょう。外微分作用素 d^k:Ω^k(M)→Ω^k+1(M) に対して、内積に関する随伴線形写像 δ^k = (d^k-1)^† :Ω^k(M)→Ω^k-1(M) が定義できます。(... - Ω^-1(M) ← δ⁰ - Ω⁰(M) ← δ¹ - Ω¹(M) ← δ² - Ω²(M) ← δ³ ← ...) は、もとのド・ラーム複体とは矢印の向きと番号付けが変わっています*2。こちらを随伴ド・ラーム複体〈adjoint de Rham complex〉と呼びましょう。ド・ラーム複体と随伴ド・ラーム複体を一緒に書くと、次のような感じです。

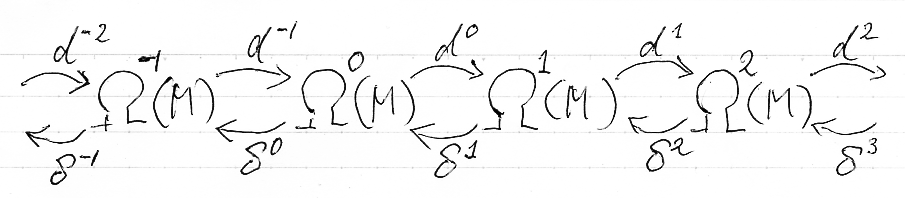
適当なkに注目して、d^k-1δ^kとδ^k+1d^kを考えます。d^k-1δ^kもδ^k+1d^kも、道順は違いますが、Ω^k(M)から出て戻ってくる作用素（線形写像）になります。d^k-1δ^k, δ^k+1d^k :Ω^k(M)→Ω^k(M) ですね、下の図を見てください。

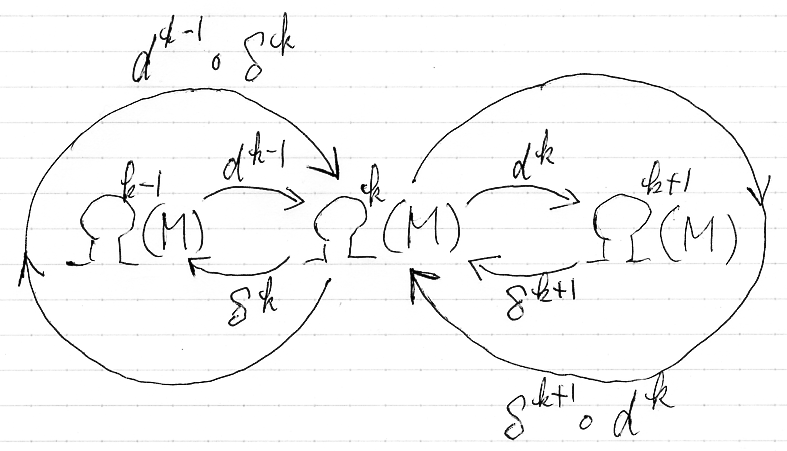
d^k-1, δ^k, δ^k+1, d^k を使って、k次のラプラシアン〈Laplacian of degree k〉Δ^kを次のように定義します。

• Δ^k := d^k-1δ^k + δ^k+1d^k :Ω^k(M)→Ω^k(M)

反図式順結合記号''と添字は、煩雑なのでしばしば省略されます。

• Δ := dδ + δd

ユークリッド空間Rⁿの標準座標系を使って Δ⁰:Ω⁰(Rⁿ)→Ω⁰(Rⁿ) を陽に表示すると、それは古典的ラプラシアンに（符号は気にしなければ）一致します。（ラプラシアンについては、最後の節にも説明があります。）

Ω^k(M)の部分ベクトル空間Θ^k(M)を次のように定義します。

• Θ^k(M) := {α∈Ω^k(M) | Δ^k(α) = 0}

α∈Θ^k(M) のとき、αを（M上の）調和k-形式〈harmonic k-form〉と呼びます。特に調和0-形式を調和関数〈harmonic function〉と呼びます。Θ^k(M)は、M上の調和k-形式の空間です。調和形式とド・ラーム複体／随伴ド・ラーム複体／ド・ラーム・コホモロジーのあいだには次の関係があります。

• H^k(M) Θ^k(M)
• Ω^k(M) = Im(d^k-1)_⊥Im(δ^k+1)_⊥Θ^k(M) （_⊥は直交直和を表す）

k次のド・ラーム・コホモロジーは、調和k-形式の空間と同型であり、k-形式の空間は、“外微分作用素の像空間”と“随伴外微分作用素*3の像空間”と“調和形式の空間”に直交直和分解します（ホッジ分解）。

今、ザーッと述べたことは、例えば次の本『微分形式の幾何学』にチャンと書いてあると思います（持ってるけど、ほとんど読んでない）。

微分形式の幾何学

複体

「複体〈complex〉」という言葉は、色々な分野・文脈で使われます。「簡単なモノを素材として出来上がる、より複雑なモノ」といった意味です。ここでは、複体を幾何複体、組み合わせ複体、代数的複体の3種に分けます。

• 幾何複体〈geometric complex〉は、「簡単な図形を素材として出来上がる、より複雑な図形」です。
• 組み合わせ複体〈combinatorial complex〉は、幾何複体の組み合わせ構造を抽出して、図形の点集合としての側面を忘れたものです。
• 代数的複体〈algebraic complex〉は、（前節を読んだのなら； ド・ラーム複体や随伴ド・ラーム複体のような）ベクトル空間と作用素（線形写像）の系列のことです。

この記事では、幾何複体は正式には定義せずに、絵を描いて済ませる（お茶を濁す、ともいう）ことにします。絵は、我々の目と心が認識するだけの対象物で、対応する組み合わせ複体をオフィシャルに扱います。組み合わせ複体から代数的複体は機械的な手順で作られます。したがって、幾何複体、組み合わせ複体、代数的複体は密接に関連していて、あまり区別しなくても（ほぼ同一視しても）問題は少ないと思います*4。

幾何複体の具体例を挙げておきます*5（下図）。この図形は、多様体の模倣ではなく、もっと自由気ままな図形です。

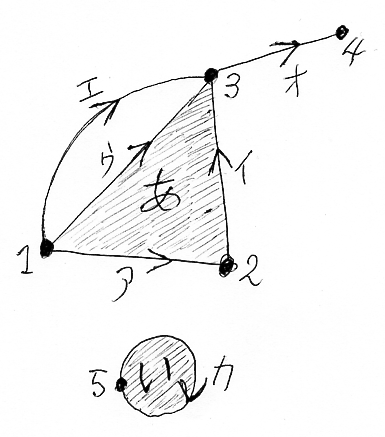
幾何複体の素材となる簡単な図形をセル〈cell〉と呼びます。

• 0次元セル： 点のこと
• 1次元セル： 線分のこと
• 2次元セル： 多角形のこと

k次元のセルを短くk-セル〈k-cell〉とも呼びます。0-セルは頂点〈vertex〉、1-セルは辺〈edge〉、2-セルは面〈face | area〉とも呼びます。

複体のセルには前もって向き〈orientation〉を与えておきます。「セルの向き」という概念には微妙なところがあります。セルの向きに関して2つの解釈が可能です。

1. セルの向きは、幾何複体の重要な特徴であり、セルの向きが変わると異なる複体とみなす。
2. セルの向きは、便宜的なものであり、セルの向きが変わっても、複体としては同じとみなす。

二番目の場合、注目しているのは向きを無視した図形であり、記述や計算の都合から向きを適当に割り当てている、ということです。ここでは、二番目の立場をとります。向きが最初からあるわけではなくて、人為的・無根拠に割り当てたとします。しかし、一度割り当てた向きは変えません。

さて、とりあえずは向きを便宜的に割り当てたとします。その後で、幾何複体が持つ幾何構造としての向きを定義することができます。他のセルの境界（の一部）ではないセルに、本来の向きが便宜的向きと一致しているかどうかを符号で指定します。セルの形状ごとに、そういう指定方法を考える必要があります*6。いずれにしろ実際の応用では、下部構造である便宜的向きの上に、上部構造として本来の向きを指定することになると思います。

複体上のパスとチェーン

Kが幾何複体だということは、Kが各次元のセルから構成されているということです。前節の例で言えば：

• Kの頂点＝0-セルの集合 = K₀ = {1, 2, 3, 4, 5}
• Kの辺＝1-セルの集合 = K₁ = {ア, イ, ウ, エ, オ, カ}
• Kの面＝2-セルの集合 = K₂ = {あ, い}

便宜上、k = 0, 1, 2 以外では、K_k = {} と定義します。これにより、任意の k∈Z に対して集合K_kが決っていることになります。集合K_kの要素は、図形としてのセルというより、セルに貼り付けたラベルの集合ですが、ここでは、ラベルと図形を同一視して語ります。

複体Kの、順序付けられた辺の列 [e₁, e₂, ..., e_ℓ] で、e_iの終点 = e_i+1の始点 （1 ≦ i ＜ ℓ）を満たすものをパス〈path | 道 | 経路〉と呼びます。次はパスの例です。

• [ウ, オ, -オ, -イ, -ア, エ, -イ]

ここで、マイナス符号'-'は辺を逆向きに辿ることを意味します。例えば [オ, -オ] の部分は、順方向に頂点3から頂点4に行って、逆方向に頂点4から頂点3に戻ることを示します。通過する頂点の列は、[1, 3, 4, 3, 2, 1, 3, 2] です。ただし、頂点を並べても、パスの記述にはなりません。[1, 3] だけでは、辺ウを通ったか辺エを通ったか不明です。

パスは、その辺に順序があるのでリスト・データでした。順序を無視してしまうと、次の集合になります。

• {ウ, オ, -オ, -イ, -ア, エ, -イ}

純粋な集合なら、二回出現する'-イ'は一回につぶせます。しかし、ここではマルチ集合〈multiset | bag〉とみなして、さらに符号の効果も考慮します。

1. 順序は問題ではない。自由に符号付き辺を並べ替えてよい。
2. 同じ辺がプラス（順行）とマイナス（逆行）で出現したらキャンセルして無くなる。
3. 同符号の同じ辺が複数回出現しても、それをつぶす（重複を除く）ことは出来ない。

次のような計算ができます。

  {ウ, オ, -オ, -イ, -ア, エ, -イ}
 // アイウエオ順でソート
= {-ア, -イ,  -イ, ウ, エ,  オ, -オ }
 // オ, -オ を消去
= {-ア, -イ,  -イ, ウ, エ}
 // -イ, -イ をまとめる
= {-ア, -2イ, ウ, エ}

{-ア, -2イ, ウ, エ} は、形式的な和を使って -ア + (-2イ) + ウ + エ あるいは、-ア - 2イ + ウ + エ とも書けます。先に提示した計算ルールは、和の記法と完全に整合します。

結局、ア, イ, ウ, エ, オ, カ に整数係数を付けて足し算した形になります。この形を整数係数のチェーン〈chain with integer coefficients〉と呼びます。整数係数のチェーンでは、当たり前の方法で足し算と整数スカラー倍ができます。例えば：

  (2ア + 5エ - カ) + (イ - 2エ + カ)
= 2ア + 5エ - カ + イ - 2エ + カ
= 2ア + イ + 5エ - 2エ - カ + カ
= 2ア + イ + (5 - 2)エ + (-1 + 1)カ
= 2ア + イ + 3エ + 0カ
= 2ア + イ + 3エ

  3(2ア + 5エ - カ)
= 3・2ア + 3・5エ - 3カ
= 6ア + 15エ - 3カ

パスは、図形の上を走る道／経路として具体的なイメージを持てます。それに対してチェーンは、天下りに代数的に定義されるので、幾何的イメージを持ちにくいものです。パスの素材である“向き付き辺”をバランバランにして、足し算できるようにしたモノ、くらいに考えてください。パスが持つ情報の一部は失われますが、その代わりチェーンの計算は自由にできます。

実数係数チェーン空間

前節で整数係数のチェーンを考えましたが、係数は形式的なものなので、実数係数にすることもできます。x_ア, x_イ, x_ウ, x_エ, x_オ, x_カ を勝手な6つの実数として、形式的なスカラー倍と和：

• x_アア + x_イイ + x_ウウ + x_エエ + x_オオ + x_カカ

を考えればいいのです。例えば、ア + √2イ + πエ - オ はそのような形式的な和です。

このような形式的な線形結合達は、全体として実数体上のベクトル空間を形成します。こうして作ったベクトル空間を実数係数チェーン空間〈chain space with real coefficients〉と呼びます。その要素である形式的な線形結合は実数係数チェーン〈chain with real coefficients〉ですね。以下、係数は常に実数とするので、「実数係数」は省略します。

チェーン空間は、もとになった幾何複体Kから決まるものです。そこで、C₁(K) と書きます。ん？ 下付きの1は何でしょうか？ 今定義したチェーン空間は、1次の（または1次元の）チェーン空間であり、他に0次のチェーン空間、-1次のチェーン空間、2次のチェーン空間などもあります（後述）。

複体Kに対する1次のチェーン空間は、Kの1-セル＝辺の集合K₁から自由生成された自由ベクトル空間です。集合Sからの自由ベクトル空間をR^Sと指数形式で書くとして：

• C₁(K) := R^K₁

我々の具体例においては、

• C₁(K) := R^K₁ = R^{{ア, イ, ウ, エ, オ, カ}} R⁶

複体Kに対して、0次のチェーン空間C₀(K)は、1次と同様に定義します。

• C₀(K) := R^K₀

我々の具体例においては、

• C₀(K) := R^K₀ = R^{{1, 2, 3, 4, 5}} R⁵

ここで、表記上のちょっとして問題が発生します。事例のC₀(K)は、集合{1, 2, 3, 4, 5}から生成されるので、自然な基底も{1, 2, 3, 4, 5}です。基底の要素1, 2に実数係数2, -3を付けて足すと 21 + (-3)2 = 21 - 32 となりワケワカリマセン。この問題を回避するためによく使われるのは物理起源のケットベクトル記法で、2|1> + (-3)|2> = 2|1> - 3|2> のように書きます。ここでは、もっと安直に長さ1のリストのように書いて 2[1] - 3[2] としましょう。辺の線形結合も、[ア] + √2[イ] + π[エ] - [オ] のように書いてもかまいません。

k = 0, 1, 2 以外の次数（または次元）kについても、

• C_k(K) := R^K_k

としてk次のチェーン空間を定義します。

我々の例では、k = 0, 1, 2 以外では、K_k = {} だったので、

• C_k(K) := R^K_k = R^{} R⁰ = {0}

となり、C_k(K)（k = 0, 1, 2 以外）はゼロベクトル空間になります。

境界作用素 1

幾何複体Kに対して、k次のチェーン空間C_k(K)が定義できました。ベクトル空間C_k(K)の要素は、k次のチェーン〈chain of degree k〉、あるいはより短くk-チェーン〈k-chain〉と呼びます。0-チェーンは0-セル＝頂点の形式的線形結合、1-チェーンは1-セル＝辺の形式的線形結合、2-チェーンは2-セル＝面の形式的線形結合でした。

これから、k-セルに(k-1)-チェーンを対応させる写像 B_k:K_k→C_k-1(K) を考えます。具体例を先に見ておきましょう。

我々の具体例である複体において、1-セルeに対してB₁(e)を次のように定義します。

e	B1(e)
ア	[2] - [1]
イ	[3] - [2]
ウ	[3] - [1]
エ	[3] - [1]
オ	[4] - [3]
カ	[5] - [5] = 0

これは、1-セル＝辺の両端となる頂点に符号を付けて足した（引いた）もので、次のようにも書けます。

• B₁(e) = eの終点 - eの始点

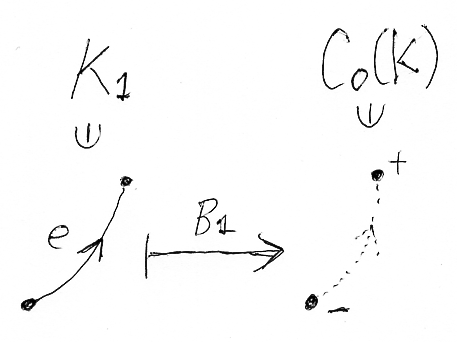
一般の1-チェーン、つまり1-セル＝辺の線形結合に対しては、上記定義を線形に拡張します。例えば：

  B1(ア + イ + オ)
= B1(ア) + B1(イ) + B1(オ)
= ([2] - [1]) + ([3] - [2]) + ([4] - [3])
= [2] - [1] + [3] - [2] + [4] - [3]
= [4] - [3] + [3] + [2] - [2] - [1]
= [4] - [1]

  B1(-ウ + 2エ)
= B1(-ウ) + B1(2エ)
= -B1(ウ) + 2B1(エ)
= -([3] - [1]) + 2([3] - [1])
= -[3] + [1] + 2[3] - 2[1]
= [3] - [1]

B₁に慣れるには、幾つかの例を計算してみるのが一番です。パスに対応するチェーン [ア] + [イ] + [オ]（上で計算済み）とか [エ] + [オ] + (-[オ]) + (-[イ]) などのB₁値を計算すると両端の差が出るはずです。また、[ア] + [イ] + (-[ウ]) のような一周するパスに対応するチェーンでは結果がゼロになるはずです。

写像 B₁:K₁→C₀(K) 、あるいは線形写像としての B₁:C₁(K)→C₀(K) を、1次の境界作用素〈boundary operator〉と呼びます。「境界」と呼ぶことは、計算例から納得できると思います（納得できるまで事例を計算してください）。

我々の具体例では、C₁(K) R⁶、C₀(K) R⁵ だったので、B₁:C₁(K)→C₀(K) は5行6列の行列で表示できます。その具体的な形は：

[tex:

B1 = \begin{pmatrix}


1 & 0  & -1 & -1 & 0  & 0 \\
1  & -1 & 0  & 0  & 0  & 0 \\

0  &  1 & 1  & 1  & -1 & 0 \\

0  &  0 & 0  & 0  & 1  & 0 \\

0  &  0 & 0  & 0  & 0  & 0 \\

\end{pmatrix}

]

ソフトウェアで行列計算してみましょうか。すぐ上の手計算をMaximaに計算させると次のようです。

B1 : matrix(

            [-1,  0, -1, -1,  0, 0],

            [ 1, -1,  0,  0,  0, 0],

            [ 0,  1,  1,  1, -1, 0],

            [ 0,  0,  0,  0,  1, 0],

            [ 0,  0,  0,  0,  0, 0]);

B1 . [1, 1, 0, 0, 1, 0] /* 1, 2, 3, 4を通るパスの境界 */;

B1 . [0, 0, -1, 2, 0, 0] /* パスではないチェーンの境界 */;

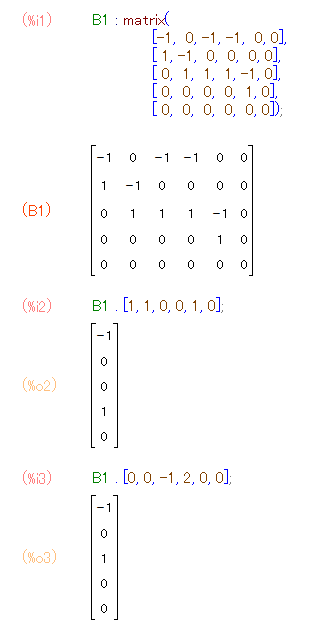
境界作用素 2

2-セル＝面xに対しては、B₂(x)を次のように定義します。

x	B2(x)
あ	[ア] + [イ] - [ウ]
い	[カ]

この定義は、図形としての面[あ]と面[い]の境界（周り）を1-チェーンとして表現していることになります。

面[あ]と面[い]の形式的線形結合である2次のチェーン（C₂(K)の要素）には、上記の定義を線形に拡張します。

  B2(-[あ] + 2[い])
= B2(-[あ]) + B2(2[い])
= -B2([あ]) + 2B2([い])
= -([ア] + [イ] - [ウ]) + 2([カ])
= -[ア] - [イ] + [ウ] + 2[カ]

具体例における2次の境界作用素B₂を行列表示すれば：

[tex:

B2 = \begin{pmatrix}

1  & 0 \\

1  & 0 \\


1 & 0 \\
0  & 0 \\

0  & 0 \\

0  & 1 \\

\end{pmatrix}

]

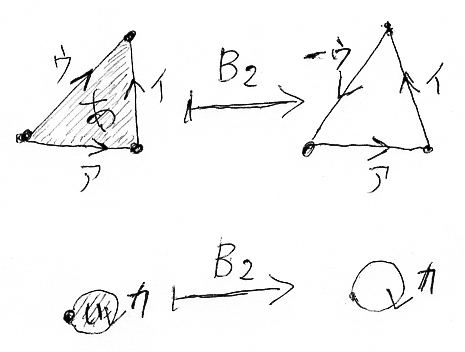
上の手計算をソフトウェアでやってみれば次のようです。

B2 : matrix(

            [1,  0],

            [1,  0],

            [-1, 0],

            [ 0, 0],

            [ 0, 0],

            [ 0, 1]);

B2 . [-1, 2];

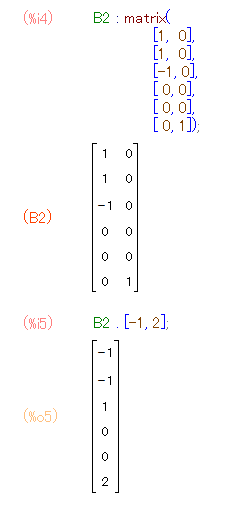
B₁とB₂のあいだには、極めて重要な次の関係が成立しています。

• B₁B₂ = 0

右辺の0はゼロ線形写像のことです。具体例で確認をしてみます。

B1 . B2;

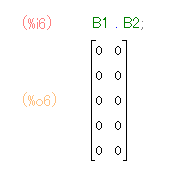
B₁B₂ = 0 の幾何的意味は次のように述べることができます。

• 1次元高い図形の境界となっているような図形には、もはや境界はない。

この事実は、次元によらずに成立すべきことで、一般的には次の形になります。

• B_k-1B_k = 0

我々の具体例では、k = 2, 1 以外のB_k（例えば、B₃, B₀）はゼロ線形写像なので、確かに（自明に）すべてのkで、B_k-1B_k = 0 です。

この記事の第3節「複体」において、複体という言葉は色々な場面で少しずつ違った意味で使われる、と言いました。B_k-1B_k = 0 という等式は、「複体」全般に共通する大原則なのです。幾何複体、組み合わせ複体、代数的複体のいずれも、この等式「境界には境界がない」で統御されています。

さて、今まで、境界作用素について具体例を使って説明してきました。一般的な定義はしていません。これから一般的な定義をする … かと言うと、しません。出来ません。境界の定義は、幾何セル（図形としてのセル）の形状によって扱いが変わります。幾何セル／幾何複体は絵を描いて済ませているこの記事では、正確な議論は出来ないのです。

境界作用素B_kを実際どう定義するか、の話題は割愛せざるを得ないのですが、どのように定義したにしろ、B_k-1B_k = 0 は成立する必要があります。成立するように定義するのです。

組み合わせ複体と代数的複体

Kが幾何複体だとすると、Kはセルという基本図形から構成される複合図形でした。そして、Kのk-セルの集合をK_kと書きました。実のところ、このK_kは図形の集合というよりはラベルの集合で、「ラベルと図形を同一視」することで、我々の心に“図形のイメージ”を持ち続けよう、という方針でした。

この“図形のイメージ”を捨て去れば、(K_k | k∈Z)は単に整数で番号（インデックス）付けられた集合族に過ぎません。ただし、集合の族だけでは、次元ごとに素材を書き並べているだけで、素材どうしの繋がり具合の情報が全くありません。組み合わせ的な繋がり具合／隣接関係の情報は、境界作用素として抽出することができます。つまり、組み合わせ複体は、「Z-インデックス付き集合族 ＋ 境界作用素の族」となります。

k次の境界作用素は、B_k:K_k→Z^K_k-1 という形で定式化できます。ここで、Z^K_k-1は、K_k-1の要素（セルのラベル）を整数係数で線形結合したチェーンの集合（Z-加群という構造を持ちます）でした。

今回、スカラーは実数と決めているので、B_k:K_k→Z^K_k-1 は、B_k:K_k→R^K_k-1 へと係数拡張して使いました。後から実数にするなら、最初から実数係数で考えて、「k次境界作用素は B_k:K_k→R^K_k-1 として与えられる」としたほうが手っ取り早いですね。

そんなこんなを考慮して、組み合わせ複体の正式な定義を与えましょう。(K_k, B_k | k∈Z) が組み合わせ複体〈combinatorial complex〉だとは：

1. k∈Z に対して、K_kは有限集合（空集合でもよい）。
2. K_k ≠ (ゼロ空間) であるkは有限個しかない。
3. k∈Z に対して、B_kは K_k→R^K_k-1 という写像。
4. k∈Z に対して、B_k-1B_k = 0 が成立する。

1番と2番の条件で、セル（のラベル）の総数が有限であることが保証され、神ならぬ人間／コンピュータでも取り扱い可能となります。「負次数（負次元）のセルがない」も条件に入れることが多いですが、これは気にしないことにします。

定義の上では、境界作用素B_kは K_k→R^K_k-1 として与えられます。しかしこれは、自明な線形拡張により B_k:R^K_k→R^K_k-1 という線形写像とみなせます。K_k→R^K_k-1 でも R^K_k→R^K_k-1 でも大差ないので、同じ記号B_kを使います。（圏論をご存知なら、R^(-)によるモナドのクライスリ圏とクライスリ結合を考える、と言えば察しが付くでしょう。）

B_kとB_k-1の結合は、B_k-1を線形写像 B_k-1:R^K_k-1→R^K_k-2 と考えて、B_k:K_k→R^K_k-1 の後に*7結合すれば、B_k-1B_k:K_k→R^K_k-2 が出来ます。あるいは、最初から線形写像どうしの結合と考えてもいいです。

等式 B_k-1B_k = 0 の左辺は今説明した結合写像〈composed map〉であり、右辺は常にゼロベクトルの値を取るゼロ写像です。k-セル x∈K_k での値を考えるなら、等式は次の形です。

• B_k-1(B_k(x)) = 0 in R^K_k-2

境界作用素B_kをすべて線形写像と考えると、組み合わせ複体Kから、ベクトル空間 C_k(K) := R^K_k と 線形写像 B_k:C_k(K)→C_k-1(K) のZ-インデックス付き族 (C_k(K), B_k | k∈Z) が得られます。これは代数的複体〈algebraic complex〉です。

組み合わせ複体から、ただちに代数的複体（ベクトル空間と線形写像の系列）が得られました。組み合わせ複体Kと対応する代数的複体(C_k(K), B_k | k∈Z)は、ほとんど同じものです。しかし、組み合わせ複体から独立した、純粋な代数的複体を考えることができるし、純粋な代数的複体を調べておいたほうがいいでしょう。次節で述べます。

代数的複体もっと

代数的複体は、チェーン複体〈chain complex〉と呼ばれることが多いのですが、「チェーン複体」はかなり曖昧な使い方がされる言葉なので、「代数的複体」という言葉を使って話を進めます。

代数的複体は、Zで番号付けられた無限個のベクトル空間V_k達と、隣り合ったベクトル空間のあいだの線形写像の列f_k達から構成されます。線形写像の向きによって、二種類に分けます。

• 共変代数的複体： f_k:V_k→V_k-1 と、番号が減る方向が線形写像の向き。
• 反変代数的複体： f_k:V_k→V_k+1 と、番号が増える方向が線形写像の向き。

共変／反変という形容詞は、代数的複体を圏論（の関手圏）で定式化すれば、合理的な意味を持ちます。が、今は気にしなくていいです。番号は、次数〈degree〉、次元〈dimension〉、階数〈grade | 位数〉など、色々と呼び名がありますが、これも気にしてもしゃーないです。まー、どうでもいい、と。

前々節で強調したように、複体と呼ばれるからには、次の条件が成立しています。

• 共変代数的複体： f_k-1f_k = 0
• 反変代数的複体： f_k+1f_k = 0

これらの条件を満たすようなベクトル空間／線形写像の無限列がそれぞれ、共変代数的複体〈covariant algebraic complex〉、反変代数的複体〈contravariant algebraic complex〉で、それらを総称して代数的複体〈algebraic complex〉と（ここでは）呼びます。

この定義だけだと、茫漠としていて何が嬉しいかサッパリ分かりませんが、線形代数を一般化した理論（ホモロジー代数）を展開できます。ベクトル空間より弱い構造である加群を考えたり、付加的な条件（例えば有界性、有限性）を付けたりします。

定義から感じるもうひとつの疑問： 共変代数的複体と反変代数的複体ってほぼ同じなのに、なんで2種類あるんだ？ 2種類いらんだろう、と。実は、両方を一度に考えることがあるので、必要なんですよ。

(V_k, f_k) が共変代数的複体だとします。f_k:V_k→V_k-1 と、番号が減る方向です。ベクトル空間V_k達の双対ベクトル空間と、線形写像f_k達の双対線形写像を考えます。すると：

• (f_k)^*:(V_k-1)^*→(V_k)^*

W_k := (V_k)^* と置けば：

• (f_k)^*:W_k-1→W_k

と、番号が増える方向の線形写像の列ができます。番号付けをちょっと変えて、g_k-1 := (f_k)^* （g_ℓ := (f_ℓ+1)^*）とすると：

• g_ℓ:W_ℓ→W_ℓ+1

(W_ℓ, g_ℓ)は、反変代数的複体となります。(W_ℓ, g_ℓ)は(V_k, f_k)の双対なので、ペアとして一緒に扱うことになります。

共変／反変の別を、番号添字を下付き／上付きで区別する習慣があります。しかし、絶対的なルールはないので、その場その場で、どのような番号付け・添字ルールを採用しているかを確認するしかないです。

そもそも、「チェーン複体」あるいは形容詞なしの「複体」が、共変代数的複体と反変代数的複体のどちらを指しているかは場面・文脈に依存しているので、なんとも言えません。「チェーン複体」とは反変代数的複体かも知れないし、共変代数的複体かも知れないし、両者を総称してるかも知れないし、あるいは、多様体や幾何複体から作った具体的代数的複体を指しているかも知れません。

ラプラシアンとラプラス方程式

電磁気、流体、熱伝導などの分野では、ラプラシアン〈Laplacian | Laplace operator〉と呼ばれる微分作用素が登場します。

これは直交座標系で書いたラプラシアンΔですが、ベクトル解析では、grad（勾配）とdiv（発散）を使ってラプラシアンを書きます。

現象の記述として、ラプラシアンを使った（偏微分）方程式 Δf = g （ポアソン方程式）が出てきます。現象が特別に単純な場合は、Δf = 0 となり、これをラプラス方程式〈Laplace equation〉（斉次〈せいじ〉ポアソン方程式）と呼びます。

僕は物理に無知なんで、ホントのところよく分からんのですが、特別に単純な現象を表現するラプラス方程式の解とは、次のようなものらしいです。

• 電磁気： 電荷がない自由空間における電位（電気的ポテンシャル）の場
• 流体： 非圧縮性流れの速度ポテンシャル場
• 熱伝導： 熱源がない場合の定常熱伝導の温度分布場

ん？ 話題が突然変わったような？ -- いや、そうでもないんです。物理現象そのものは、僕には理解も説明もできませんが、使われる方程式を整理すると代数的複体のなかで定式化できる、という話なんです。第2節と同様、代数構造として抽出蒸留される前の背景を述べてます。

現象が起きる舞台である空間をMとします。Mはn次元の多様体ですが、n = 2 または 3 のユークリッド空間だと思ってもいいです。Mの上には、様々な量の場があります。量の場とは、ベクトル解析で扱う対象なんですが、これがねー、なんだかワケワカランのですよ。

「ベクトル解析ワケワカラン！」という話は過去にしています。次の記事達（古い順）とそこからリンクされている他の記事達に書いてあります。

• テンソル：なぜ難しいのか
• なんとかならないのか!? ベクトル解析：用語法の無茶苦茶
• 伝統的テンソル計算を理解するヒント
• 雑談の効能：スピノールとか

要約すると、「反変ベクトル、共変ベクトル〈コベクトル | 余ベクトル〉、極性ベクトル、軸性ベクトル（擬ベクトル）とかって、何なんだよ、あれは！ フザケンナヨ、わっかんねーよ」です。

なぜ分かりにくいのかと言うと、ベクトル解析で扱う量（の場）はスカラー（場）とベクトル（場）なのですが、なし崩しに「ベクトルつっても、2種類あるかもな」だの「スカラーつっても、密度はちょっと違うかな」だのと言い出して、量の分類が不明瞭なのです。

空間M上の量の分類を整理すると、第2節で触れたド・ラーム複体と随伴ド・ラーム複体になります。

• Mのド・ラーム複体： … → Ω^-1(M) - d^-1 → Ω⁰(M) - d⁰ → Ω¹(M) - d¹ → Ω²(M) - d² → Ω³(M) - …
• Mの随伴ド・ラーム複体： … → Ω³(M) - δ³ → Ω²(M) - δ² → Ω¹(M) - δ¹ → Ω⁰(M) - δ⁰ → Ω^-1(M) - …

Mのド・ラーム複体は、反変代数的複体であり、随伴ド・ラーム複体は共変代数的複体です。ちなみに、ここで使われている形容詞「反変／共変」は圏論由来であり、「反変ベクトル／共変ベクトル」とは関係ありませんから要注意。

Mのド・ラーム複体と随伴ド・ラーム複体はペアになりますが、（前節で説明したような）線形代数の意味での双対になっているわけではなくて、ベクトル空間の内積によりペアを形成します。双対ペアじゃなくて随伴ペアです。ここらへんの代数的メカニズムは、次回に説明します。

ド・ラーム複体と随伴ド・ラーム複体により、ベクトル解析を明瞭に再定式化すると、grad, div, curlなどの微分作用素は、外微分作用素d^k／随伴外微分作用素〈ベルトラミ作用素〉δ^kに置き換えられます。そして、ラプラス方程式は次の形に一般化されます（第2節で既出）。

• (d^k-1δ^k + δ^k+1d^k)α = 0 （α∈Ω^k(M)）

k = 0 の場合が、特別に簡単な電位場／速度ポテンシャル場／温度分布場などを記述する方程式です。一般化されたラプラス方程式の k = 1 のときは、ベクトル解析の言葉で書くなら次のようになるようです。

• curl curl X - grad div X = 0

関数（スカラー場）に限らず、一般の微分形式（ベクトル場の双対となる場）にまで通用するラプラシアンの定義 Δ := dδ + δd *8を誰が発見したか僕は知りません。歴史的事実はワキに置いて、一般化ラプラシアンを表す言葉には、ド・ラーム〈de Rham〉、ベルトラミ〈Beltrami〉、ホッジ〈Hodge〉の名前を適当に混ぜて冠すればいいようです（例： ラプラス／ベルトラミ作用素、ラプラス／ド・ラーム作用素、ホッジ／ラプラス作用素）。

一般化ラプラシアン／ラプラス方程式は、代数的複体の枠組み内で定義できるわけですが、逆に、一般化ラプラシアン／ラプラス方程式により、代数的複体の構造を記述・分析できます。ラプラシアン／ラプラス方程式に現象的イメージをお持ちの方は（僕はダメですが）、代数的複体の構造にもヴィヴィッドな描像を得られるのではないでしょうか。

---

次回は実際に、ラプラシアンを道具に、代数的複体の構造を記述・分析します。現象を背景としたヴィヴィッドな描像を伝えることは僕には出来ませんが、代数的複体への線形代数的アプローチを説明したいと思います。

• 次回：ド・ラーム・コホモロジーとホッジ分解のオモチャ (2/2)

*1:最初にf, 次にgの順序での結合（合成）を、f;gと書くのが図式順、gfと書くのが反図式順です。

*2:番号付けを変えるのは単なる習慣です。習慣に反しますが、δ^k = (d^k)^†:Ω^k-1(M)→Ω^k(M) としたほうがスッキリする場面もあります。

*3:δは、余微分作用素〈codifferential operator〉と呼ばれることが多いですが、この言葉は混乱を招くので、随伴外微分作用素としておきます。後（次回）でベルトラミ作用素〈Beltrami operator〉という言葉も使います。

*4:ここでの「問題」はコミュニケーション上の問題のことで、「概念的に区別しなくてもよい」ということではありません。

*5:当初、この事例に関して露骨な計算〈explicit calculation〉を全てやるつもりでしたが、気力が萎えてやめました。

*6:メビウス・バンドのように、原理的に向きを割り当てられない図形もあります。

*7:図式順記法なら、「後に」は右になり、反図式順記法なら、「後に」は左になります。

*8:添字の省略と補完をうまくやる前提で、dd = 0, δδ = 0 なので、Δ := (d + δ)² とも書けます。