このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

分布から拡散へ： ミシェル・ジリィを巡って

雑記／備忘

確率・統計の概念・用語には、不明瞭なものが多くて難儀します。こういった不明瞭さに対して、きわめてクリアな解釈を与えてくれる道具にジリィモナド〈Giry monad〉があります。

ところが、ジリィモナド周辺もかなりとっ散らかった印象があります。ジリィモナドには多様なバリエーションがあるのですが、それらを包括的に語る言葉が不足しています。

物理現象である“拡散”をメタファーにすると、ジリィモナドを直感的に把握できるようになり、用語法の整理にも寄与することになります。

内容：

分布を寄せ集めると

以前、「確率分布」って言葉の意味が分からないなー、と嘆いていました。結果的に言えば、確率分布の意味は“確率測度または確率密度関数”です。そのどちらを意味するかは文脈によるし、ニュアンスを含めることもあります。

曖昧性やニュアンスがあることで分かりにくい言葉になっていますが、一方で、曖昧ゆえに使い勝手がいい言葉でもあります。

さて、分布のフォーマルな定義は一旦脇に置いて、分布という言葉の直感的な印象、あるいは雰囲気にについて語ります。

分布というからには、なにか空間的に広がっている印象がありますよね。Yが空間だとして、「yがYの点だ」とは、yが、点集合としてのYの要素ということです。一点yは分布していません。物理的に言えば、質量1の質点みたいなものです。

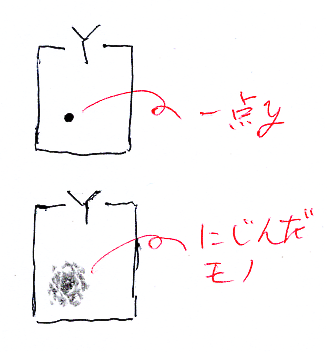
それに対して分布したモノは、一点ではなく、滲〈にじ〉んで広がっています。空間にモヤッと物質が存在する感じです。質点とは限らない物質は、その質量密度関数で記述できるでしょう。よって、分布を密度関数と同一視するのは悪くないと思えます。

Yの一点とは、単元集合〈singleton set〉 1 = {0} からYへの写像と言っても同じです。f:1→Y と f(0)∈Y は1：1に対応しますから。そうなると、分布は、写像 f:1→Y が滲んで広がってしまったモノとみなせます。

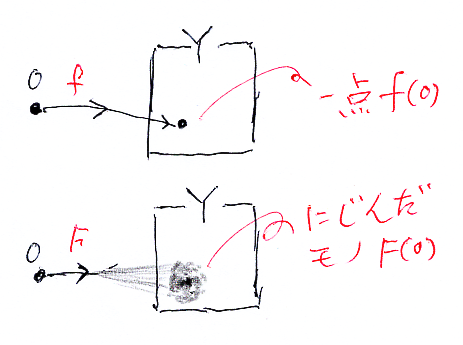
いま、別な空間Xを持ってきて、写像 f:X→Y を考えます。x∈X に対して f(x) はYの点です。確定した一点です、滲んでません。もし、f(x) が滲むと、Xの各点xに対して、Y上の滲み（あるいは物質）が対応することになります。点xに対応する滲みが F(x) です。

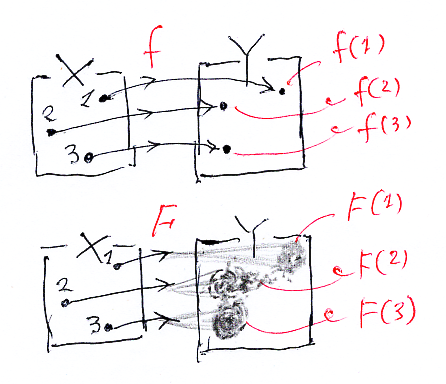
上の図では、Xの点が３つしか描いてありませんが、もっとたくさんの点があってもいいです。むしろ、Xに無限個の点があるほうが普通でしょう。無限かもしれないXの各点に、Y側の滲み（あるいは物質）が対応する状況です。各点ごとの分布が寄せ集まった状況とも言えます。

ローヴェアとジリィの定式化

Xの点でパラメトライズされた、Y上の滲み（あるいは物質）の集まり -- これをうまく定義する方法はウィリアム・ローヴェア*1〈William Lawvere〉により提案され、ミシェル・ジリィ〈Michèle Giry〉*2によりキチンと定義・調査されました。

空間Y上の確率分布〈probability distribution〉をすべて集めた集合をPDist(Y)と書きましょう。いま出た「確率分布」は雰囲気的なモノではなくて、確率論の意味での確率分布 -- つまり確率測度または確率密度関数のことです。

ローヴェア／ジリィのアイディアは、F:X→PDist(Y) という写像を使う、というものです。F:X→PDist(Y) は、Xの各点xに対して、Y上の確率分布 F(x) を対応させます。Y上の確率分布は、Y上に広がったモノ／滲んだモノ／物質（総質量は1）などの定式化になっています。

いま説明したような F:X→PDist(Y) を何と呼ぶか？ これが実に困った状況でして、「ライプニッツの微分記法とアインシュタインの総和規約を測度に使ってみる」で言ったように、山のように呼び名があります。

  1. stochastic map
  2. stochastic kernel
  3. stochastic relation
  4. stochastic matrix （台集合が有限のとき）
  5. probabilistic mapping
  6. probabilistic relation
  7. probabilistic matrix （台集合が有限のとき）
  8. regular conditional probability
  9. conditional probability density
  10. Markov kernel
  11. Markov matrix （台集合が有限のとき）
  12. transition probability
  13. transition probability density
  14. transition kernel
  15. transition matrix （台集合が有限のとき）
  16. probabilistic channel
  17. stochastic channel

このブログ内で使ったことがある呼び名は：

  1. 確率写像〈probabilistic mapping〉
  2. 確率関係〈stochastic relation〉
  3. 測度的積分核〈measure-theoretic integral kernel〉
  4. マルコフ行列〈markov matrix〉

測度的積分核は、確率写像／確率関係より広い意味で使っています。マルコフ行列は、扱う空間が有限集合のときの言葉です。

ちなみに、ローヴェア／ジリィのアイディア／定式化に（ゆるく）関係する過去記事には次があります（古い順）。

  1. 何故にあえて確率を学ぶのか？
  2. 測度的積分核と随伴構造
  3. 合同を持つ圏と測度空間の圏
  4. 質量モナド
  5. ライプニッツの微分記法とアインシュタインの総和規約を測度に使ってみる
  6. 同時確率分布の圏
  7. 同時確率分布の圏の使用例：超具体的
  8. アブダクションと確率的推論
  9. 確率的推論・判断の計算法：マルコフ・テンソル絵算
  10. 余可換コモノイド・モダリティ事件の解説

話を戻して、F:X→PDist(Y) を何と呼ぶか？ -- X = 1 = {0} のときはY上の分布なので、分布と関連する言葉／親和性がある言葉がいいんじゃないのかな、と僕は思いました。

「拡散」がよくね

分布と同様に、広がって滲む感じの言葉？ 「余可換コモノイド・モダリティ事件の解説」で、分散〈dispersion〉という言葉は使ったことがあります（否定的に「非分散的」として）。溶解〈disolution〉も同じ雰囲気です。でも、拡散〈diffusion〉が一番よく使いそうです。

ローヴェア／ジリィの F:X→PDist(Y) を拡散〈diffusion〉、あるいは拡散写像〈diffusion {map | mapping}〉と呼んではどうでしょう。

雰囲気はあってますよね。でも、物理的現象として拡散現象があるし、拡散方程式なんて偏微分方程式もあります。そういう意味での拡散と、ローヴェア／ジリィのアレが乖離していると、「拡散」という言葉を割り当てるのはよろしくない気がします。

そこで、物理現象のモデルとしての拡散について調べてみました。ちら見しただけで、理解はできませんが、どうやら拡散過程〈diffusion process〉とはマルコフ過程〈Markov process〉の一種のようです。拡散過程を特徴付ける重要な等式として、チャップマン／コルモゴロフ方程式〈Chapman-Kolmogorov equation〉というものがあるようです。

その他に、遷移確率(密度)〈transition probability (density)〉、条件付き確率密度〈conditional probability density〉なんて言葉も拡散の話に出てきます。ローヴェア／ジリィと同じ用語が出てくるなー。なんか関連があると思っていいのかな。

ジリィの原典を眺めると

現在、ジリィの論文はインターネット上にもあります*3。

最初の一文がイキナリ：

The aim of this paper is to give a categorical definition of random processes and provide tools for their study.

この論文の目的は、確率過程を圏論的に定義して、それらを調べる手段を提供することである。

random processって確率過程、それがジリィの目的だったのか。すぐにマルコフ過程の話になり、圏論的な結合〈composition〉を定義する等式はチャップマン／コルモゴロフ方程式だと述べています。

えっ、これは拡散過程の話とモロカブリじゃん。ジリィの本来の意図からしても、F:X→PDist(Y) は拡散過程の遷移記述だとみなしてよさそうです。ローヴェア／ジリィが定義した圏Pの射を拡散写像と呼ぶなら、確率過程は、順序構造により圏とみなしたNやR≧0からPへの関手となります。もっとも単純（原子的）な遷移のステップがPの射＝拡散写像となります。

ジリィはまた、次のようにも語っています。

As F. W. Lawvere already pointed out in an unpublished paper [3] in 1962, most problems in probability and statistics theory can be translated in terms of diagrams in these Kleisli categories.

ローヴェアが、1962年の未出版の論文で既に指摘しているように、確率や統計のほとんどの問題は、これらのクライスリ圏内の図式による表現へと翻訳できる。

うん、これはホントだと思う。

で、上記引用内の未出版の論文とは、ローヴェアがおこなったセミナーの資料です。"the highly referenced seminar handout notes"ということで、カーク・スターツ（Kirk Sturtz）が、書き込みが入った紙資料をスキャンして公開しています。

スターツは、「確率変数」と言うのはやめようと言った人です。スターツ自身、ローヴェア／ジリィ路線の論文を何編も書いています。

ジリィ・スタイルのモナド

さて、既に山のように同義語があるのに、新しい言葉が欲しかった理由を説明しましょう。

既存の用語の多くには、stochastic, probabilistic, probability が含まれます。確率的ということですが、それは全空間の測度が1を意味します。しかし、全空間の測度が1でない状況も扱いたいのです。となると、残る言葉は（正規表現で書けば）、{Markov | transition} {kernel | matrix} です。{kernel | matrix}は、表現・表示の手段であり、圏の射そのものを表すには不適切な気がします。以前僕が使っていた測度的積分核も同じ理由でよくありません。

結局、既存用語はどれも不合格です。今後は、拡散写像〈diffusion {map | mapping}〉を採用します。拡散写像を射とする圏は、拡散写像の圏〈category of diffusion {maps | mappings}〉または単に拡散圏〈diffusion category〉と呼ぶことにします。

拡散圏を定義するには、ジリィ・スタイルのモナド〈Giry-style monad〉の説明が必要です。モナドが定義できれば、拡散圏はそのクライスリ圏として定義できます。

現在ジリィモナドと呼ばれているモノは、特定のモナドではなくて、一群のモナド達の総称です。ジリィ自身、可測空間をベースにするモナドとポーランド空間をベースにするモナドの二種類を定義しています。

まず、基礎となる圏Hを選びます*4。Hは、可測空間と可測写像の圏Measへの忘却関手（忠実関手） U:H→Meas を持つとします。ジリィは、H = Meas と H = Polish（ボーランド空間と連続写像の圏）を扱っています*5。H = (距離空間と連続写像の圏) とかでもいいでしょう*6。

Hの対象Xは可測空間とみなせるので、X上のすべての測度の集合Meas(X)を考えることができます。Meas(X)の部分集合を次のように定義します。

  • Meas<∞(X) = (有限測度の全体)
  • Meas1(X) = (確率測度の全体)
  • Meas≦1(X) = (劣確率測度の全体)

劣確率測度〈subprobability measure〉とは、全空間の測度が1以下になる測度のことです。

これらの測度の集合に対して、構造を入れたり制限をしたりすることにより、圏H上の自己関手 G:H→H を作ります。さらに、モナド単位とモナド乗法を定義して、モナド G = (G, η, μ) に仕立てます。もとにした測度の集合により、次のように分類します。

HやGの作り方は多様なので、今述べた枠組みで作られるモナドを総称してジリィ・スタイルのモナド〈Giry-style monad〉と呼ぶことにします。ジリィ・スタイルのモナドのサブ分類として、上記の三種のモナド種別があり、そのインスタンスとして具体的な個々のモナドがあります。

Hが基礎となる圏〈base category | ground category〉だとして、GがH上のジリィ・スタイルのモナドのとき、クライスリ圏Kl(H, G)が（H上の）拡散圏です。Gが確率ジリィモナドのときは、Kl(H, G)を確率圏〈{stochastic | probabilistic} category〉と呼ぶことがあります。

ジリィモナドの相対化

前節で述べた枠組みで、基礎となる圏Hとその上のジリィ・スタイルのモナドGの選び方・作り方を変えれば、色々な拡散圏・確率圏を定義できます。目的に応じてカスタムメイドの圏を構成できるでしょう。

しかし、重要な事例でも前述の枠内に収まらないものがあります。FinSetを有限集合と写像の圏として、H = FinSet とします。このとき、H上のジリィ・スタイルのモナドをうまく作れません。有限集合のあいだの拡散写像はとても重要なので、これは困ります。

こんなときは相対モナド〈relative monad〉の出番です。相対モナドでは、台関手が自己関手でなくてもモナド類似構造を作れます。有限集合FinSetの場合ならば、例えば距離空間の圏Metに対して、埋め込み J:FinSet→Met を前提して、台関手Gを G:FinSet→Met の形に構成できます。

H = FinSet は離散有限な場合になるので、一般の（連続無限を含む）場合と比較するのは有用です。（[追記]縦と横を逆にしました。[/追記]）

離散有限な場合 一般の場合
有限集合 可測空間／位相空間
写像 可測写像／ボレル写像／連続写像など
横縦ベクトル 測度（分布）
縦横ベクトル 非負実数値関数
行列 積分核
スカラー積 積分
非負実数係数行列 拡散写像の積分核
マルコフ行列 確率拡散写像の積分核

通常のモナドでは、台関手に自己関手が必要で、そのためにある程度の規模の圏が必要です。相対モナドでは、J:H→C のような関手を仮定した上で、台関手は G:H→C の形でよく、FinSetのような小規模の圏を基礎の圏に取れます。モナドとして相対モナドまで許せば、ジリィ・スタイルのモナドとそのクライスリ圏（それが拡散圏）の応用範囲はさらに広がるでしょう。

資料

先に挙げた2つの原典は古い資料なので、もう少し新しいものを紹介します。

パナンガデン〈Prakash Panangaden〉の論文は、計算科学を意識して書かれているので、読みやすいと思います。次の2つの論文は、用語法を変えているだけで内容はほとんど同じです。

拡散写像には、反転〈converse | 転置〉と双対性という重要な話題があります。それについては、次の2つの論文に書いてあります。それぞれ、計算科学と統計への応用が意図されています。

　

エフェクト論理の観点からジリィモナドや積分について語っているものとして：

確率拡散写像を各著者がどう呼んでいるかというと：

  • ローヴェアは probabilistic mapping
  • ジリィは transition probability
  • スターツは conditional probability
  • パナンガデンは probabilistic relation と Markov kernel
  • ドバーカット〈Doberkat〉は stochastic relation
  • ドールクゥイスト〈Dahlqvist〉達は kernel
  • ヤコブス〈Jacobs〉は特に呼び名を付けてないようです。

ところで、拡散というと、空気中に広がる煙とか、水に溶けるインクとかを思い出すのですが、実写とCGを組み合わせた次の動画がすごい。[追記]残念ながら消失。[/追記][さらに追記]似た動画を見つけたのでURL差し替え。[/さらに追記]

*1:今まで、「ローヴェル」と表記してきたのですが、「ローヴェア」のほうがもとの音に近いようなので、「ローヴェア」にします → https://ja.forvo.com/word/william_lawvere/ 。Wikipeia項目も「ローヴェア」ですし。

*2:名前から判断するに、フランス人の女性でしょう、たぶん。

*3:存在は知っていても読めなかった論文なのでありがたいのですが、当該サイトが公開の権利を持っているかどうかはあやしいです。

*4:Hはジリィが使っていた記法です。

*5:ジリィの記号ではMesとPol。

*6:確率測度の空間上への距離の導入が必要になりますが、ハッチンソン距離〈Hutchinson {metric |distance}〉やワッサースタイン距離〈Wasserstein {metric |distance}〉が使えるでしょう。