論理の限量子 -- つまり全称限量子(記号は'∀')と存在限量子(記号は'∃')-- の使い方が分からない、という質問・相談を受けることがあります。なかでも、「∀と∃の順序を交換してイイの? それともダメなの?」はFAQ〈Frequently Asked Question〉でして、ここ1年でも4回聞かれた気がする。
内容:
like関係
論理式の意味や使い方を、日常生活や自然言語の比喩的事例を使って説明するのはヨロシクナイと僕は思っています。しかし、最初のとっかかりに関しては、比喩的事例も致し方ないですね。人間関係の記述を例題にします。
A, B, C, D の4つの要素を持つ集合Xを考えます。
- X = {A, B, C, D}
A, B, C, D は4人の人だと思ってください。集合Xは、サークルとか家族とか会社の部署とか、人間の集団です。そう思うとリアルで生々しくなるでしょ。でも、別に生々しくなくてもいい方は、単なる集合と要素だと思ってください。
集合Xの2つの要素のあいだの関係として、love〈愛している〉とかを出すと生々しさが過ぎるので、like〈好き〉という関係にしましょう。x, y∈X について、like(x, y) の意味は「xさんはyさんを好きである」だとします。「自分を好き」も意味を持つので、like(x, x) もあります。「好き」は対称的な関係ではないので、like(x, y) と like(y, x) は同じではありません。
現実世界では、好き(like(x, y) が真)か好きでないか(like(x, y) が偽、¬like(x, y) が真)をハッキリ決めるのは難しいですが、ここでは、x, y∈X に対して like(x, y) が完全に確定しているとします。この確定したlike関係を記述・表現するために3つの方法を使います。
- 有向グラフ
- 表〈テーブル〉
- 碁盤目
like関係の記述・表現
有向グラフ
A, B, C, D を平面内の4点(有向グラフのノード)として描きます。like(x, y) が真のとき、xからyへの矢印を描きます。例えば、「AさんはBさんを好き」なら like(A, B) が真なので、点Aから点Bへの矢印を描きます。次は、そうやって描いた有向グラフの一例です。
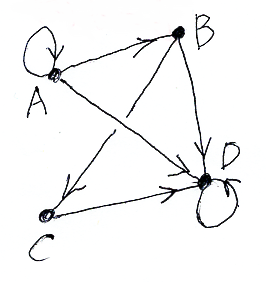
表〈テーブル〉
like(x, y) を表〈テーブル〉にすることもできます。横方向にx、縦方向にyをとるとして、like(x, y) が真ならマル、偽ならバツを記入することにします。
| y↓x→ | A | B | C | D |
|---|---|---|---|---|
| A | ◯ | ☓ | ☓ | ☓ |
| B | ◯ | ☓ | ☓ | ☓ |
| C | ☓ | ◯ | ☓ | ☓ |
| D | ◯ | ◯ | ◯ | ◯ |
表の欄は、直積集合 X×X の要素に対応します。欄が16あるのは、X×X が16要素を持つからです。
- X×X = {A, B, C, D}×{A, B, C, D} =
{(A, A), (A, B), (A, C), (A, D), (B, A), (B, B), (B, C), (B, D),
(C, A), (C, B), (C, C), (C, D), (D, A), (D, B), (D, C), (D, D)}
マルをtrue, バツをfalseと思えば、この表は X×X→{true, false} という関数〈写像〉の値を記述した表です。実際、likeはそのような関数とみなせるので、関数likeを表〈テーブル〉で記述・表現したことになります。
碁盤目
まず、縦に4本、横に4本の線を引いて、16個の交点(格子点)ができるようにします。碁盤目ですね。表の場合と同じように、各格子点が (A, A), (A, B), ..., (D, D) を表します。そして、like(x, y) が真である格子点 (x, y) に色を塗るとかマーカーを付けるとかします。
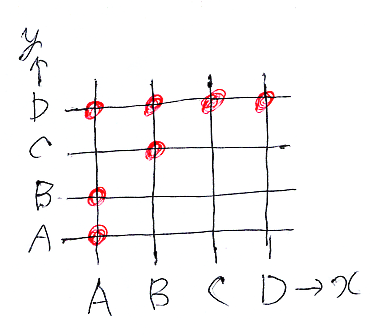
マークされた点達は、X×X の部分集合になります。この場合は:
- {(A, A), (A, B), (A, D), (B, C), (B, D), (C, D), (D, D)}
7個の要素からなる部分集合です。表のマルの数も7個だし、有向グラフの辺も7本でした。
碁盤目にマークする描き方は、likeを X×X の部分集合とみなす発想です。集合らしく最初の文字を大文字*1にして Like と書くと、Like ⊆ X×X で、(x, y)∈Like であることを like(x, y) と書くわけです。
他の例も
以上、特定のひとつの例に対して、有向グラフ/表/碁盤目で表現してみました。ここから先でも同じ例を使い続けます。が、他の例はいくらでも作れます。集合を {A, B, C, D} に固定しても、この集合上のlike関係は色々とあります。
例えば、碁盤目の16個の格子点から適当に点を選んでみれば、それが別な事例になります。自分で作った事例を調べてみることが、論理式や限量子に慣れる良い練習になります。
誰からも好かれる人
集合 X = {A, B, C, D} をサークルだと考えましょう。サークルのなかに、
- 誰からも好かれる人
がいるかも知れません。aさんが誰からも好かれることは、次のように書けます。
- ∀x∈X.like(x, a)
日本語で言えば:
- サークルXのメンバーはみんなaさんが好き。
「みんな」を使いましたが、「誰でもが」「全員が」「どんな人も」とかでも同じです。堅苦しい言い方なら「任意のメンバーは」となります。日本語のニュアンスは関係ありません。
今出てきた「aさん」は、誰と特定されているわけではないですが「とある誰かさん」という意味です。このような目的で使う変数aは自由変数です。それに対して変数xは全称記号'∀'と結びついて使用されているので束縛変数です。
自由変数/束縛変数にどんな文字を使ってもかまいませんが、ここでは、a, b, c などを自由変数、x, y, z などを束縛変数に使うことにします。これは、単にこの記事でのローカルな習慣で意味はありません。
サークルX内に「誰からも好かれる人」がいることは次のように書けます。
- ∃y∈X.∀x∈X.like(x, y)
我々の例では、Dさんが実際に誰からも好かれているので、上の命題は真になります。別な例を作れば、同じ命題が偽になるかも知れません。
好きな人はいますか?
前節の命題 ∃y∈X.∀x∈X.like(x, a) の、存在限量子と全称限量子の順序を変えると:
- ∀x∈X.∃y∈X.like(x, y)
内側の ∃y∈X.like(x, y) は、xさんには好きな人がいることです。xを自由変数aに書き換えてみれば:
- ∃y∈X.like(a, y)
堅苦しく言えば:
- サークルXの誰かyさんが存在して、aさんはyさんを好き。
もう少し素直な日本語にすれば:
- aさんには、サークルXのメンバーで好きな人がいる。
日本語の表現としては、束縛変数の名前は入れないほうが自然ですね。僕が「自然言語(日本語)を使って説明する/理解する」のがあまりヨロシクナイと思うのは、日本語の文法とか表現の多様さ・機微とかに注意が向いてしまい、論理のドライな骨格が見えにくくなるからです。日本語表現に注意を向けるのはやめてね。
さて、∃y∈X.like(a, y) の自由変数aをxに書き換えて全称記号で束縛する(外側に ∀x∈X. を付ける)と:
- ∀x∈X.∃y∈X.like(x, y)
日本語で言えば、
- サークルXの全員が、サークルXのメンバーで好きな人がいる。
前節の命題:
- サークルX内に、誰からも好かれる人がいる。
とはだいぶ違います。
好きな人は一人だけ
∀x∈X.∃y∈X.like(x, y) を否定してみます。限量子に関するド・モルガンの法則で順次変形していくと:
- ¬∀x∈X.∃y∈X.like(x, y)
- ∃x∈X.¬∃y∈X.like(x, y)
- ∃x∈X.∀y∈X.¬like(x, y)
最後の命題を日本語で言うなら:
- サークルXの誰のことも好きではない人が、サークルX内にいる。
我々の事例でそんな人はいるでしょうか? -- いませんね。では、好きな人が一人しかいない人はどうでしょう? これはいますね。CさんとDさんです。
Cさんは、誰からも好かれているDさんを好きですが、Dさん以外は自分自身も含めて好きではありません。Dさんは、自分しか好きではありません。にも関わらず、誰からも好かれています。不思議だ(フィクションですからね)。
aさんが、好きな人が一人しかいないことを論理式で表すのはけっこう難しいです。aさんが好きな相手をbさんとします。すると:
- like(a, b)
bさん以外(x≠b)は好きではないので、
- ∀x∈X.(x≠b ⇒ ¬like(a, x))
内部の含意論理式の対偶をとってもいいです。
- ∀x∈X.(like(a, x) ⇒ x = b)
こっちは、「好きならばそれはbさん」ってこと。
以上から、aさんはbさんだけを好きなことは:
- like(a, b)∧∀x∈X.(like(a, x) ⇒ x = b)
bさんの正体が明らかではなくて、そんな人がサークルX内にいる(存在する)よ、ってことなら:
- ∃y∈X.(like(a, y)∧∀x∈X.(like(a, x) ⇒ x = y))
これで、aさんが“単推し”(一人だけを好き)の人であることが表現できます。ただし、Dさんのように好きな相手が自分であってもかまいません。
自由変数aを束縛変数に変えて、さらに'∃'または'∀'を付けることができます。
- ∃z∈X.∃y∈X.(like(z, y)∧∀x∈X.(like(z, x) ⇒ x = y))
これは、サークルX内に“単推し”の人がいるよ、です。我々の例では真です。一方、
- ∀z∈X.∃y∈X.(like(z, y)∧∀x∈X.(like(z, x) ⇒ x = y))
サークルXのメンバーは全員が“単推し”だ、ということで、我々の例では真ではありません。実際、Aさん、Bさんは複数の人を好いています。「誰のことも好きではない人」がいても、この命題は偽になります。
言霊は困るんだけど
日常生活の複雑な事情、日本語表現の多様さや微妙な違いなどは、ドライな判断を惑わしたり、余計な感情を呼び起こすので、論理的に考えたいときは出来るだけ排除したい要素です。
以前、次の記事を書きました。
人に豊かなイメージをもたらす日本語の機能を“言霊”と呼んでいるのですが、これが大変に邪魔になる、という話です。
ですが、そもそも'∀'と'∃'の入り口でモヤモヤしている人は、日常と日本語からのエモーションの力を借りてでも一歩前に進めれば、まっ、いいかな。
*1:こういう習慣は何の意味もありませんけどね。集合を小文字で書いても何も悪いことはないので。