圏論では、点と矢印の図〈dots-and-arrows diagram〉を使って計算や証明をすることがよくあります。通常目にする図式は、組版や印刷の都合から、単色でレイアウトも平面的です。でも、手描きするなら、色を付けたり、立体的に描いたりするとだいぶ分かりやすくなりますよ。
内容:
図式の可換性と等値核の例
点(対象を表す)と矢印(射を表す)からなる図が可換〈commutative〉だとは、その図の任意の二点間を結ぶ有向パス(矢印を繋いだ道)がどれも同じ射を表すことです。可換図式は、幾つかの等式と同じことなんですが、等式よりずっと簡略で視認性に優れています。
図式が可換であることを暗黙に仮定する場合が多いですが、矢印で囲まれた多角形が可換であることを明示的に表したいときは、カギの形やクルリンと回った矢印を描くことがあります。僕は、単にマル印で済ませています。
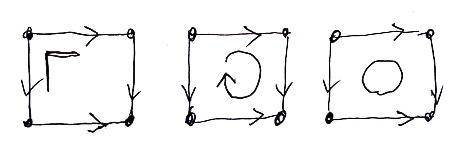
可換性を仮定しない多角形には、バツ印です。
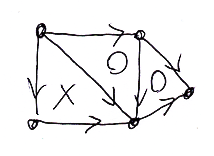
もし色鉛筆があるなら、可換な多角形は色で塗りつぶすといいですよ。塗ってないところは可換とはみなしませんが、念のためにバツ印を付けておいてもいいです。
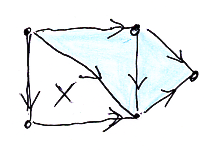
描いた後で気が付いたんですが、バツ印はエックスと紛らわしいですね。描いた本人は区別できても、他の人がエックスだと思って混乱するかも知れません。バツ印を付けるか付けないかは適宜判断してください。
さて、次の図で、共端な2つの射〈平行ペア〉f, g は可換(等しい)とは限りませんが、e;f = h かつ e;g = h 、つまり e;f = e;g です。
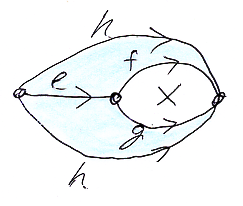
平面図では、hが2本の矢印になってますが、2本のhを重ねて立体的に描けば次のようです。

底面が二辺形であるとんがりコーン〈円錐形〉です。底面は抜けているので、頭に被れるコーンです。コーンの側面が2つの三角形で、どちらも可換なので色が塗ってあります。2つの塗った三角形が、e;f = h と e;g = h です。
抜けた底面を共有するもうひとつのとんがりコーンを持ってくると、頂点から頂点への矢印(射)が一意的に存在するとします。点線と'∃!'は、「点線の射が一意的に存在する」ことを表す目印です。
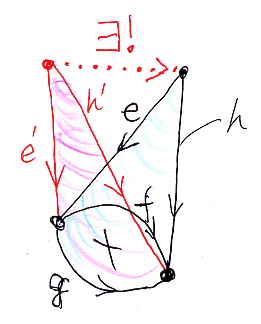
このとき、eは、f, g の等値核〈等化射 | イコライザー | equalizer〉です。実は、上の図で描いてない可換性(=塗るべき面)があるのですが、それは後で出てきます。
図式と論理記号
現状の組版・印刷の技術・コスト・習慣から、図式と論理記号を混ぜた論理式とかは使えないです。しかし、そのせいで、図式が何を意味するかが曖昧になってしまうことがあります。手描きなら、図式と論理記号のハイブリッド表現も自由ですからやってみます。
前節の等値核を集合圏で考えると、“fとgが定義する方程式の解集合”の埋め込み写像がeになります。等値核の域〈domain〉が解集合です。集合圏以外でも、等値核の域を(方程式の)解対象〈solution object〉と言っていいでしょう。
対象Xが、fとgで定義される方程式の解対象であることを、X is-solution-of (f, g) と表すことにします。これは、圏の対象・射を含む命題です -- is-solution-ofが二項述語です。fとgは共端な射であることも表すには、図式を混ぜ込んだほうがいいでしょう。
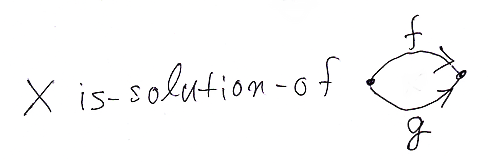
X is-solution-of (f, g) の意味は、Xから出る射eがあって、eが(f, g)の等値核であることですから:
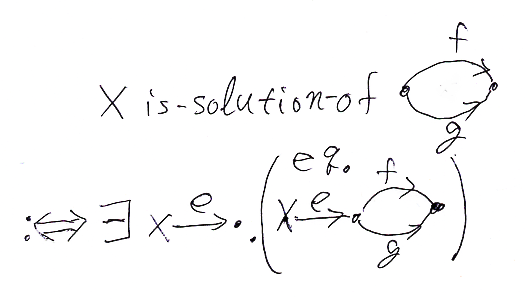
2行目の論理式に含まれる左上の'eq.'は、当該の図式が等値核図式であることを示します。等値核図式であること(is-equalizer-diagram)をちゃんと書けば次のようになります。(Xとバツ印が紛らわしいですからご注意。)
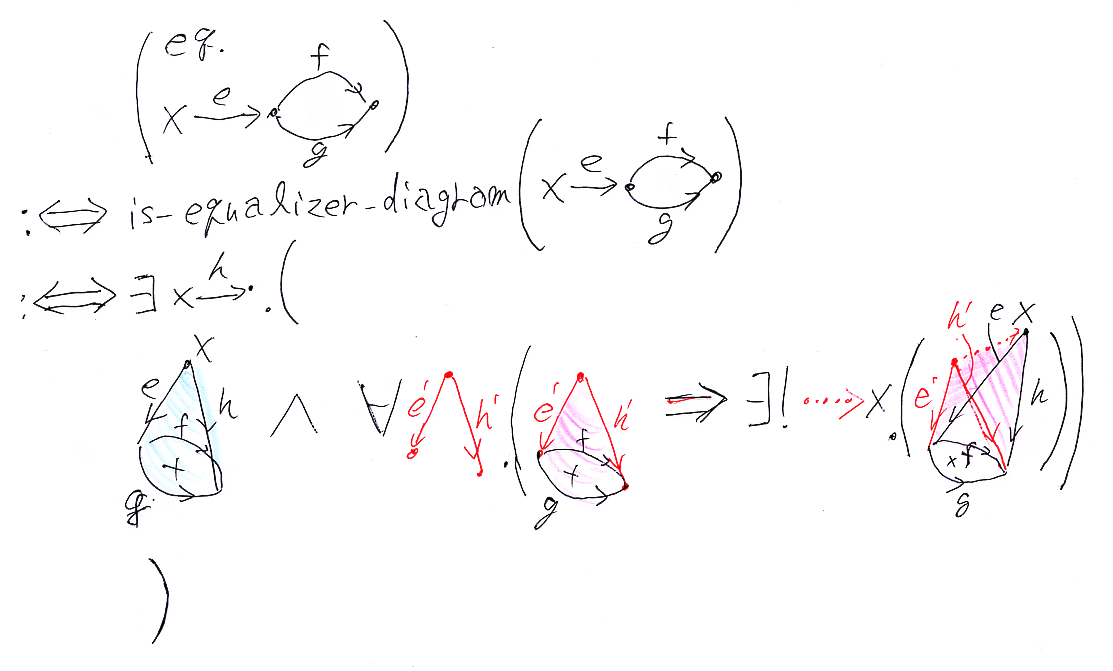
論理記号の意味は:
- :⇔ : 左(または上)側を、右(または下)側で定義する
- ∃ : …である…が存在する
- ∧ : かつ
- ∀ : 任意の…に対して…である
- ⇒ : ならば
- ∃! : …である…が一意的に存在する
図式を混ぜないテキストだけの論理式で表現するには、出てくるすべての対象・射に名前を付けなくてはなりません。
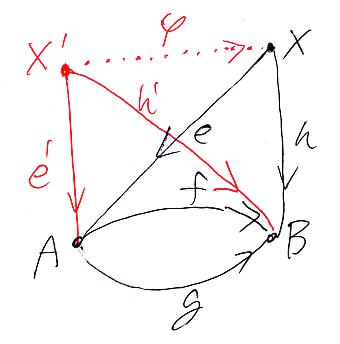
これらの名前を使って、先の3行目の論理式(図式混じり)は、次のように書けます。
∃h:X→B.(
(e;f = h ∧ e:g = h) ∧
∀e':X'→A, h':X'→B.(
(e';f = h' ∧ e';g = h') ⇒
∃!φ:X'→X.(φ;e = e' ∧ φ;h = h')
)
)ここで、φ;e = e' ∧ φ;h = h' の部分が、先に「描いてない可換性」と言った可換性です。
日本語に直訳すれば:
(e;f = h かつ e:g = h) かつ
任意の e':X'→A と h':X'→B に対して、
(e';f = h' かつ e';g = h') ならば
(φ;e = e' かつ φ;h = h') である射 φ:X'→X が一意的に存在する
ような射 h:X→B が存在する。hを消去すると少し単純になりますが、一般論(極限の概念)からすると、hを残しておいたほうが自然とも言えます。
図式は簡便でいいんですが、その簡便さにより、背後にある複雑性が隠れてしまいがちなのが問題です。たまには、テキストで明示的に書き下してみて、背後の複雑さを確認してみるといいでしょう。