テンソル記法の「意味不明問題」は解決した - 檜山正幸のキマイラ飼育記 (はてなBlog)

ん？あれ？ひょっとして … 一昨日書いた記事「なぜにテンソル記法は意味不明なのか」を読み直していて、気付いたことがあります。テンソル記法の「意味不明問題」は、解決できるようです。

思いついたときに書いておかないと、二度と書かない（書けない）ことがあるので、ふんばって必要なことは全部書いておきました。

内容：

テンソル記法の「意味不明問題」とは
アイディアと方法
インデックスからマーカーへ
テンソル空間
テンソルとプロファイル
プロファイル注釈
テンソルのテンソル積
双対空間に対するマーカー
テンソルの縮約
置換と置換が定めるテンソル
テンソルの置換同値
もうひとつの縮約
ネーム化とコネーム化
インデックスとしての添字

テンソル記法の「意味不明問題」とは

テンソルの書き方〈記法〉としては、伝統的記法をそのまま採用します。「 $x^{i \,\alpha}_j$ はテンソルである」のような言い方を許容します。書き方・言い方においては、伝統を尊重することにして、問題はそれらが意味する実体は何か？です。意味がなんだか分かんないじゃないか -- と愚痴ったのが一昨日の記事「なぜにテンソル記法は意味不明なのか」です。

例えば、次のような言い方はほんとのところ、何を意味しているのでしょう？

x はテンソルである。
x は3階のテンソルである。
$x^{i \,\alpha}_j$ はテンソルである。

背後にベクトル空間や線形写像を想定したとき、書かれた／発話された言葉を背後のベクトル空間／線形写像と正確に結びつけることが出来ないのです。結びつけることが出来るにしても、そこで使われる技法は暗黙的であり、明示的な定義やアルゴリズムではありません。

困るじゃないか、ダメじゃないか -- これが、テンソル記法の「意味不明問題」です。

アイディアと方法

テンソル記法の「意味不明問題」を解決するために使うアイディアは次の2つです。

上付き添字〈superscript〉、下付き添字〈subscript〉の解釈を、インデックスからマーカー（後述）に変える。
マーカーに対して、双対を表す構文（ここではマイナス記号）を導入する。

一番目は既に使われているかも知れません。二番目の構文は僕は見たことがありません（でも、どこかの誰かが使っているかも）。

新規の構文〈シンタックス〉は以上の2つです。構文（書き方）に対する意味〈セマンティクス〉は、公理的・抽象的な線形代数により与えます。基底は一切使いません。 $x^{i \,\alpha}_j$ のような伝統的記法は、基底の選択・固定を前提にしていますが、上付き添字／下付き添字の解釈を変えるので、基底は不要になります。

念の為に注意すると；上付き添字／下付き添字を基底と関連付ける方法が無意味だとか不要だとは言ってません。具体的な計算では必須な方法です。今回は「基底を使わない解釈と方法を採用するよ」ってだけです。

基底を使わない公理的・抽象的な線形代数は、抽象性ゆえに難しいです。この難しさを緩和するために、アブラムスキー〈Samson Abramsky〉やクック〈Bob Coecke〉によるお絵描き線形代数を使います。アブラムスキー／クックは、線形代数としての量子力学（あるいは、量子力学としての線形代数）を絵図〈picture | graphic | diagram〉で記述しています。アブラムスキー／クック流の描き方*1で絵を描くことにします。お絵描き量子力学／お絵描き線形代数を事前に知っている必要はありませんが、興味があれば次の記事をどうそ。

また、アブラムスキーによるネームとコネームという概念を使います。これに関して述べている記事は：

インデックスからマーカーへ

テンソル記法 $x^{i \,\alpha}_j$ に出現する i, j, α は、インデックス（番号やラベル）だと教えられ、そう思っているでしょう。まず、その発想をやめましょう。i, j, α は、番号やラベルの集合上を動くのではなくて、単なる記号です。ただし、その記号はベクトル空間と結び付いています。

ベクトル空間と結び付いた記号をマーカー〈marker〉と呼ぶことにします。マーカー（単なる記号）とベクトル空間の結び付きは、次の形で宣言することにします。

marker i, j, k for V
marker α, β, γ for W

マーカーは、ベクトル空間（の名前）の別名だと思ってください。つまり、

i, j, k はいずれも、ベクトル空間（の名前） V の別名
α, β, γ はいずれも、ベクトル空間（の名前） W の別名

ベクトル空間の別名として宣言されたマーカーの使い途は二種類あります。

テンソルのプロファイル情報を注釈するため。
テンソルに対する縮約演算を記述するため。

「テンソルのプロファイル情報」は後で説明しますが、今ここでは「注釈」という言葉に注目してください。 $x^{i \,\alpha}_j$ において、上下に配置された i, j, α は、そのレイアウトも含めて注釈になります。注釈は、情報を提供しますが、それ以上の役割を持ちません。次の等式は、省略やゴマカシなしに厳密に成立します。

$x = x^{i \,\alpha}_j$

なぜなら、注釈は（あれば助かりますが）なくてもかまわないので、すぐ上の等式の意味は、

$x = x$

なのです。こりゃ絶対に成立しますよね。さらに、次も成立します。

$x^{i \,\alpha}_j = x^{k \,\gamma}_i$

これは、「注釈を取り除くと $x = x$ 」という理由だけではなくて、注釈情報も左右同じなのです。なぜなら、i も k も Vの別名であり、α も γ も W の別名なので、別名の代わりに正式名称で注釈を書けば：

$x^{V \,W}_V = x^{V \,W}_V$

やはり絶対に成立します。

テンソル空間

テンソル空間〈tensor space〉とは、いくつかのベクトル空間のテンソル積として書かれたベクトル空間のことだとします。例えば：

V $\otimes$ W $\otimes$ V^* ： 3つのベクトル空間 V, W, V^* のテンソル積として書かれたベクトル空間
V^* $\otimes$ V ： 2つのベクトル空間 V^*, V のテンソル積として書かれたベクトル空間
W^* $\otimes$ W $\otimes$ W^* $\otimes$ W ： 4つのベクトル空間 W^*, W, W^*, W のテンソル積として書かれたベクトル空間

特別な場合として：

V ： 1つのベクトル空間 V のテンソル積（何もしない）として書かれたベクトル空間
W^* ： 1つのベクトル空間 W^* のテンソル積（何もしない）として書かれたベクトル空間

さらに特別な場合として、次のように考えます。

R ： 0個のベクトル空間のテンソル積として書かれたベクトル空間

ここで注意しなくてはならないのは、テンソル空間は、それを構成するテンソル積因子の情報を伴っていることです。「そのテンソル空間は、何個のベクトル空間をどのようにテンソル積したのか？」という質問に答えられる必要があります。例えば、V $\otimes$ W には、複数のテンソル空間構造があります。

V $\otimes$ W ： 2つのベクトル空間 V, W のテンソル積として書かれたベクトル空間
V $\otimes$ W ： 1つのベクトル空間 V $\otimes$ W のテンソル積として書かれたベクトル空間

テンソル空間を構成しているテンソル積因子の情報も書き添えて、次のように区別しましょう。

(V $\otimes$ W from V, W)
(V $\otimes$ W from V $\otimes$ W)

ユークリッド空間 R⁶ には、整数6の因数分解だけのテンソル空間構造があります*2。

(R⁶ from R⁶) （6 = 6）
(R⁶ from R², R³) （6 = 2×3）
(R⁶ from R³, R²) （6 = 3×2）

6 = 1×6 とか 6 = 2×1×3×1 まで考えるならば、

(R⁶ from R, R⁶) （6 = 1×6）
(R⁶ from R², R, R³, R) （6 = 2×1×3×1）

しかし、R によるテンソル積は R $\otimes$ V = V $\otimes$ R = V として扱うのが普通です*3。

繰り返し言うと、テンソル空間には、テンソル積因子の情報が組み込まれています。その意味で単なるベクトル空間とは違います。特別なテンソル空間として、単一のベクトル空間をテンソル積因子とするテンソル空間があります。

テンソルとプロファイル

「x はテンソルである」の正確な意味を与えましょう。テンソル〈tensor〉とは、テンソル空間のあいだの線形写像です。例えば、(V from V) から (V $\otimes$ W from V, W) への線形写像 x はテンソルです。これを次のように書きます。

x:(V from V) → (V $\otimes$ W from V, W)

単なる線形写像としての x は、

x:V → V $\otimes$ W

です。単なる線形写像として同じであっても、テンソル空間のあいだの写像としては次の2つは違います。

x:(V from V) → (V $\otimes$ W from V, W)
x':(V from V) → (V $\otimes$ W from V $\otimes$ W)

写像の余域である（(V $\otimes$ W from V, W) と (V $\otimes$ W from V $\otimes$ W)）は、テンソル空間としての構造が違うので、同じテンソル（テンソル空間のあいだの写像）とはみなさないのです。

(V from V) → (V $\otimes$ W from V, W) のような、域のテンソル空間と余域のテンソル空間の指定を（テンソルの）プロファイル〈profile〉と呼びます。この書き方は冗長なので、次のように短く書いてもいいとします。

x:V → V, W
x':V → V $\otimes$ W

プロファイルが異なるテンソル（この例では x と x'）は異なります（同じになり得ません）。

「テンソルとは、テンソル空間の要素ではないのか？」と思った人もいるでしょう。確かにそのような定義もあります。テンソル空間の要素は、特別なテンソル（線形写像）とみなせます。例えば、t∈V $\otimes$ W であり、テンソル空間としては (V $\otimes$ W from V, W) であるとします。要素 t は次の形の線形写像と1：1に対応します。

t':R→V $\otimes$ W

V $\otimes$ W をテンソル空間とみなして、テンソル t' のプロファイルを書けば：

t':R → V, W

要素 t∈V $\otimes$ W とテンソル t':R → V, W は同一視できます。ここから先は、要素を表に出さずに、対応するテンソルで話を進めます。

なお、プロファイルにおいて、「R は書かなくてもよい」という規則を採用します。これはとても便利な規則です。例えば、次のように書けます。

t': → V, W

プロファイル注釈

これですっかり準備ができました。ここからは、今までに導入した概念（マーカー、テンソル空間、テンソル、プロファイル）を使って、伝統的記法に合理的な解釈を与えます。事例としては、（R上に有限次元の）ベクトル空間 V, W を固定して、次のマーカー宣言を常に前提します。

marker i, j, k for V
marker α, β, γ for W

テンソル記法 $x^{i \,\alpha}_j$ における x はテンソルそのものであり、上下添字はプロファイル情報を注釈すると解釈します。添字を下から上に向かって読んで、x のプロファイルは V → W, W だと分かります。絵も描いてみると次のようになります。

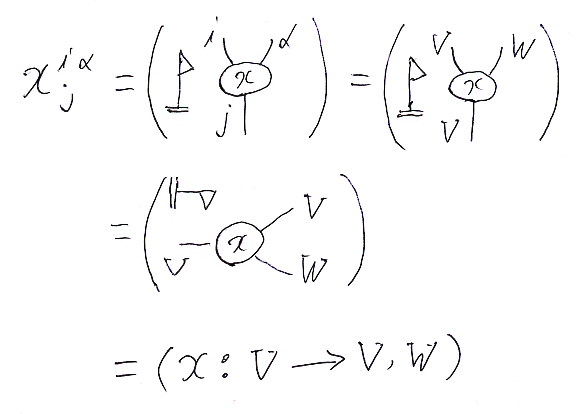
絵で、テンソル（テンソル空間のあいだの線形写像でした）は丸、四角、三角などの印で表現します。テンソル空間の因子ベクトル空間は、マーカーでラベルされたワイヤー〈ストリング〉で表します。描画の方向がさまざまなので、描画方向は“旗”で示します。

上の等式を順番に見ていくと：

見た目は伝統的テンソル記法 $x^{i \,\alpha}_j$
それを絵に描くと、x は丸、i, j, α がワイヤーになり、線形写像としての方向は下から上への方向（旗の棒の方向）。
マーカー i, j は V の別名、マーカー α は W の別名だったので、正式名称に置き換える。
描画方向を変更する。線形写像としての方向は左から右への方向（旗）。
絵からテキストに翻訳して x:V → W, W を得る。

絵と旗についてもっと詳しく知りたいなら以下の記事を参照してください。

プロファイル注釈の解釈例を幾つか追加しておきましょう。矢印の左または右に何も書いてない所はRが省略されてます。

マーカーによる注釈	対応するプロファイル情報
$z^{\alpha \, \beta\, \gamma}_{i\,j}$	z: V, V → W, W, W
$y^{k}$	y: → V
$a^{i}_j$	a: V → V
$f_{\alpha \, \beta}$	f: W, W →

テンソルのテンソル積

2つのテンソルを単に併置した場合、それはテンソル（線形写像）のテンソル積を意味するとします。例えば、

$x^{i \,\alpha}_j$ と $y^{i}$ を並べた $x^{i \,\alpha}_j \: y^{i}$ は $x\otimes y$ を意味します。もう少し詳しく書くと：

$\:\:\:\: x^{i \,\alpha}_j \: y^{k} \\ = (x^{i \,\alpha}_j) \otimes (y^{k}) \\ = (x \otimes y)^{i \, \alpha \, k}_{j}$

3行目は、テンソル x $\otimes$ y にプロファイル注釈が付いた形です。プロファイルの計算を取り出すと、次のように行なえます。

  x: V → V, W      y: → V
  -------------------------- テンソル積
   x⊗y: V → V, W, V

冗長になりますが、マーカーによる注釈と矢印によるプロファイルを両方とも書くと次のようになります。

$\: x^{i \,\alpha}_j : V \to V,W \hspace{1.5em} y^{k}: {}\to V \\ \mbox{---------------------------------------}\\ \: x^{i \,\alpha}_j \: y^{k} : V \to V, W, V$

3つのテンソルのテンソル積の例を挙げれば：

$\:\:\:\: x^{i \,\alpha}_j \: y^{k} \: f_{\beta \, \gamma} \\ = (x^{i \,\alpha}_j) \otimes (y^{k}) \otimes (f_{\beta \, \gamma}) \\ = (x \otimes y \otimes f)^{i \, \alpha \, k}_{j \, \beta \, \gamma}$

プロファイルの計算は次のようです。

$\: x^{i \,\alpha}_j : V \to V,W \hspace{1.5em} y^{k}: {}\to V \hspace{1.5em} f_{\beta \, \gamma} : W, W \to \\ \mbox{-----------------------------------------------------------------}\\ \: x^{i \,\alpha}_j \: y^{k} \: f_{\beta \, \gamma}: V, W, W \to V, W, V$

テンソル積のプロファイルを注釈するマーカーでは、同じマーカーが2個以上出現しないように気をつけてください。マーカー文字が足りないなら追加して使います。

双対空間に対するマーカー

i, j, k はベクトル空間 V のマーカーと宣言されていました。V の双対空間 V^* のマーカーはどうしましょうか。別なマーカーを宣言してもいいのですが、V のマーカーを流用することにします。単にそのまま流用しては、V と V^* の区別が付かなくなるので、次の約束をします。

V のマーカーにマイナス記号を付けた記号は V^* のマーカーとして使ってよい。

例えば、w: W^*, V → V^* というプロファイルを持つテンソルは、次のように書けます。

$w^{-i}_{-\alpha \, j}$

ここでのマイナス記号に負の数や符号反転や引き算の意味はありません。単に、双対空間のマーカーにはマイナスが付くだけです*4。

マイナス記号の約束により、「なぜにテンソル記法は意味不明なのか」に出した曖昧な例の曖昧性は解消します。

$x^{i \, \alpha}_{j} : V \to V, W$
$x^{i \, \alpha \, -j} : {} \to V, W, V^{*}$
$x_{-\alpha \, -i \, j} : W^*, V^*, V \to {}$

この3つがしばしば（意図的または不注意に）混同されるのは、密接な関係（写像とそのネーム／コネームの関係）があるからです。それについては後述します。

テンソルの縮約

伝統的記法では、同じ添字が上下に出現したら和を取ることにして、総和記号 $\sum$ を省略します。この約束（アインシュタイン規約）に、新しい解釈を与えます。

$x^{i \,\alpha}_j$ と $y^{k}$ のテンソル積は $x^{i \,\alpha}_j \: y^{k}$ ですが、j と k を同じ添字に揃えた $x^{i \,\alpha}_j \: y^{j}$ は、x と y の縮約〈contraction〉といいます。縮約を絵で描けば：

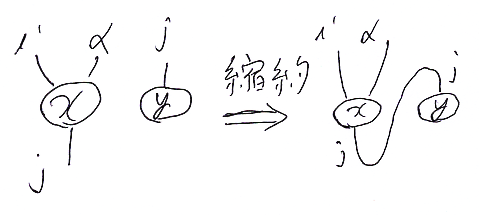
同じ名前（マーカー j）のワイヤーは繋ぎます。ワイヤーを繋ぐ操作は、抽象的線形代数のなかで基底を使わずにキチンと定義できます。以下が縮約（ワイヤーを繋ぐ操作）の定義です。

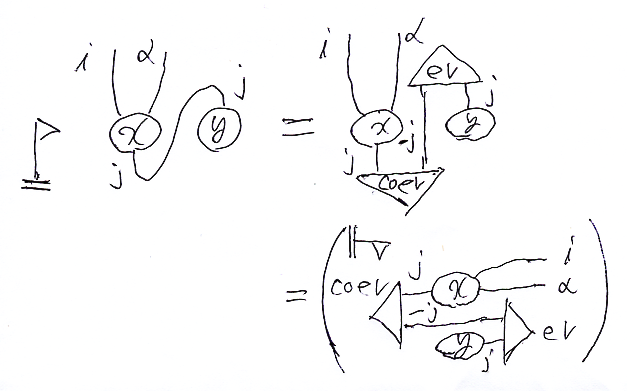
$x^{i \,\alpha}_j \: y^{j}$ は、横向きの絵からのテキストへの翻訳で $\mbox{coev};(x\otimes \mbox{id}_{V^*} \otimes y);(\mbox{id}_{V} \otimes \mbox{id}_{W})\otimes \mbox{ev}$ と書けます。セミコロンは、線形写像の結合〈合成〉の図式順記号です。ev = ev_V は、双線形なスカラー積 V^*×V → R を線形化して V^* $\otimes$ V → R とみなしたものです。coev = coev_V は ev の双対ですが、直感的には把握しにくい写像です -- が、今ここで深入りするのはやめときます。

ev, coev を使って抽象的に定義した縮約を、基底による成分表示で表現すると、実際にインデックスによる総和になっています。これは、証明が必要な定理ですが、今日は割愛します。

縮約の特別な場合として、 $a^{i}_j : V → V$ に対する $a^i_i$ を考えてみます。 $a^i_i$ の定義は次のように書けます。

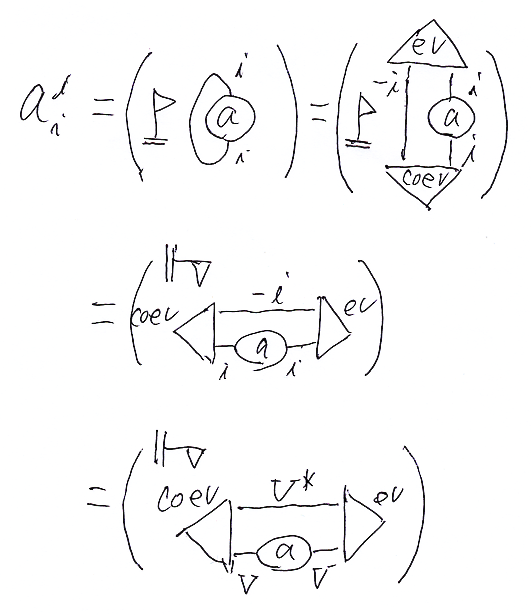
テキストで書けば、 $a^i_i = \mbox{coev};(\mbox{id}_{V^*} \otimes a);\mbox{ev}$ 。これを成分表示すると、対角成分の総和、つまりトレースになります。

置換と置換が定めるテンソル

集合 {1, 2, ..., n} 上の全単射 τ:{1, 2, ..., n}→{1, 2, ..., n} をn次の置換〈permutation of degree n〉と呼びます。n次の置換を次のように表すことが多いです。

τ = (τ(1), τ(2), ..., τ(n))

例えば、τ = (1, 3, 2) 。しかし、この書き方だと単なるタプルと区別できないので、

τ = perm(τ(1), τ(2), ..., τ(3))

とします。つまり、τ = perm(1, 3, 2) とかです。

テンソル空間 (V₁ $\otimes$ V₂ $\otimes$ ... $\otimes$ V_n from V₁, V₂, ..., V_n) があると、n次の置換 τ:{1, 2, ..., n}→{1, 2, ..., n} はこのテンソル空間からもうひとつのテンソル空間へのテンソル（線形写像でした）を定めます。τ から定まるテンソルを t とすると：

t:(V₁ $\otimes$ V₂ $\otimes$ ... $\otimes$ V_n from V₁, V₂, ..., V_n) → (V_τ(1) $\otimes$ V_τ(2) $\otimes$ ... $\otimes$ V_τ(n) from V_τ(1), V_τ(2), ..., V_τ(n))
t(v₁ $\otimes$ v₂ $\otimes$ ... $\otimes$ v_n) = v_τ(1) $\otimes$ v_τ(2) $\otimes$ ... $\otimes$ v_τ(n)

一番簡単な例は、V₁ = V, V₂ = W, τ = perm(2, 1) のときで、

t:(V $\otimes$ W from V, W) → (W $\otimes$ V from W, V)
t(v $\otimes$ w) = w $\otimes$ v for v∈V, w∈W

2つのテンソル因子を入れ替える線形写像です。線形写像はテンソルなので、置換からテンソルが定まることになります。τ = perm(2, 1) のときの t を、σ_V,W と書き、対称同型写像〈symmetry isomorphism〉とか単に対称〈symmetry〉と呼びます。なお、「対称テンソル」は別な意味なので、語尾に「テンソル」を付けたいなら「互換テンソル」〈transposition tensor〉とかでしょう。

一般に、置換 τ から上記のように定まる線形写像を、τ_{V₁,V₂, ...,V_n} と書きます。σ_V,W という書き方は、σ = perm(2, 1) として、σ_V,W = perm(2, 1)_{V, W} と考えれば辻褄が合います。

τ_{V₁,V₂, ...,V_n}:V₁ $\otimes$ V₂ $\otimes$ ... $\otimes$ V_n → V_τ(1) $\otimes$ V_τ(2) $\otimes$ ... $\otimes$ V_τ(n) と書くのは面倒なので、τ を線形写像の意味でも使って、τ:V₁ $\otimes$ V₂ $\otimes$ ... $\otimes$ V_n → V_τ(1) $\otimes$ V_τ(2) $\otimes$ ... $\otimes$ V_τ(n) とも書きます（記号の乱用）。例えば、σ:V $\otimes$ W→W $\otimes$ V 。

テンソルの置換同値

前節の議論から、任意の置換 τ は、テンソル空間のあいだの同型写像だとみなせます。σ_V,W を単に σ と書くなら、σ の（テンソルとしての）プロファイルは：

σ:V, W → W, V

同様な書き方をするなら、τ のプロファイルは、

τ:V₁, ..., V_n → V_τ(1), ..., V_τ(n)

あるいは、

τ:(V₁ $\otimes$ ... $\otimes$ V_n from V₁, ..., V_n) → (V_τ(1) $\otimes$ ... $\otimes$ V_τ(n) from V_τ(1), ..., V_τ(n))

となります。

以下、置換をあたかもテンソル（テンソル空間のあいだの線形写像）のように扱います。

テンソル計算において、置換を表現するのは難しく、混乱しがちです。添字をインデックスと解釈するなら、例えば次のような等式は意味を持ちます。

$c^{\beta \, k \, j}_{\alpha \, i} = b^{\beta \, j \, k}_{i \, \alpha}$

与えられた $b^{\beta \, j \, k}_{i \, \alpha} : V, W \to W, V, V$ から、新しい $c^{\beta \, k \, j}_{\alpha \, i} : W, V \to W, V, V$ を定義する等式とみなして絵を描くなら：

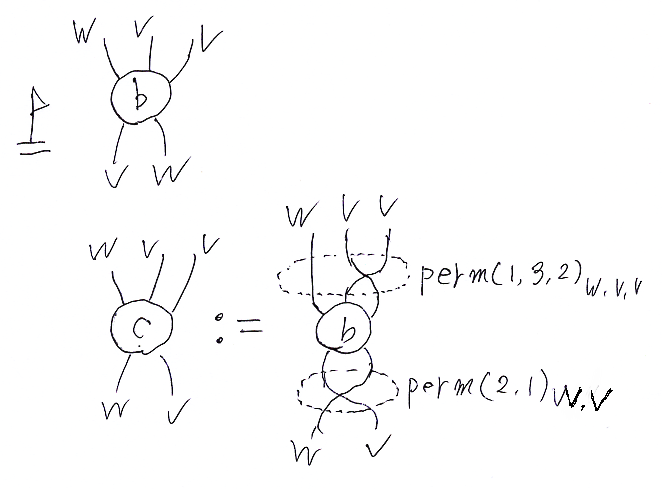
同じ状況をインデックスに頼らないで書くなら次のようでしょう。

$c := \mbox{perm}(2, 1)_{W, V};b;\mbox{perm}(1, 3, 2)_{W, V, V}$

σ = perm(2, 1), τ = perm(1, 3, 2) と置いて、簡略に書くなら：

$c := \sigma;b;\tau$

今度は、添字をマーカーによる注釈と解釈してみます。すると、

$c^{\beta \, k \, j}_{\alpha \, i} = b^{\beta \, j \, k}_{i \, \alpha}$

注釈は取り払ってもかまわないので、

$c = b$

イヤイヤッ、これは違う、ダメだ。添字の位置交換で置換を表現する方法は、添字をプロファイル注釈と解釈する方法と整合しないのです。

テンソル計算において置換は頻出します。その置換を表現するために我々は添え字を使えません。明示的に置換（から定まるテンソル）を書くしかありません。しかし一方、置換で移り合う2つのテンソルはあまり区別しない習慣もあります。そこで、置換同値という概念を定義しましょう。

2つのテンソル x と y が置換同値〈permutation equivalent〉であるとは、置換 τ, ρ があって、

y = τ;x;ρ

と書けることだとします。x ≡_perm y と書くことにします。置換は（テンソル空間のあいだの線形写像としても）可逆なので、置換同値は実際に同値関係になります。

2つのテンソル空間 (V₁ $\otimes$ ... $\otimes$ V_n from V₁, ..., V_n) と (W₁ $\otimes$ ... $\otimes$ W_m from W₁, ..., W_m) に対しても、それらが置換で移りあえるときに置換同値だとして、置換同値性を定義できます。

伝統的テンソル計算では、置換同値性を明確には意識しないままに、なんとなく置換同値なモノは同一視していたのではないかと思います。いつでも同一視しているわけでもなく、たまに区別するので困ります。

もうひとつの縮約

伝統的テンソル計算では、同じ添字が上下に現れたときに縮約を表します。我々は、このルールをそのまま採用し、基底に依存しない解釈をしました。新たに双対空間を表すマーカーを導入したので、別なタイプの縮約も定義できます。添字が同じ段（上と上、または下と下）にあっても縮約は可能です。次のルールを追加します。

同じ段（上と上、または下と下）に、マイナス記号の有無だけが違うマーカーが出現したら、それは縮約を表す。

例えば、 $w^{-i} \: x^{i\, \alpha}_{j}$ において、上側に -i と i が現れているので縮約を表します。その定義を絵で描けば：

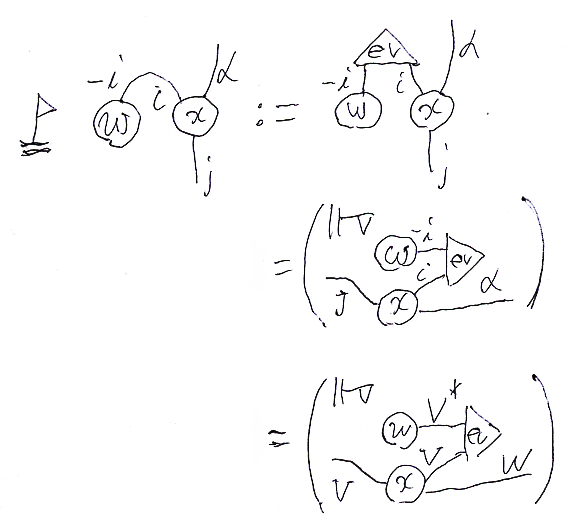
つまり：
$\:\:\: w^{-i} \: x^{i\, \alpha}_{j} \\ = (w \otimes x);(\mbox{ev} \otimes \mbox{id}_W)$

ここで、ev = ev_V は $\mbox{ev}_V : V^* \otimes V \to {\bf R}$ でした。プロファイルの計算は：
$\: w^{-i}: {} \to V^* \hspace{1.5em} x^{i\, \alpha}_{j} : V \to V, W \\ \mbox{------------------------------------------}\\ \: w^{-i} \: x^{i\, \alpha}_{j} : V \to W$

下の添字と下の添字で縮約する例も出しましょう。

$\: x^{i\, \alpha}_{j} : V \to V, W \hspace{1.5em} g^{-k}_{-j\, \beta} : V^*, W \to V^* \\ \mbox{---------------------------------------------------}\\ \: x^{i\, \alpha}_{j} \: g^{-k}_{-j\, \beta} : W \to V, W, V^*$

伝統的テンソル計算とは違って、三種の縮約が存在します。

上の添字と下の添字で縮約
上の添字と上の添字で縮約
下の添字と下の添字で縮約

ネーム化とコネーム化

伝統的記法で $x^{i \, \alpha}_{j}$ と書いた場合、それは、我々の記法で次の3つの可能性があります。

$x^{i \, \alpha}_{j} : V \to V, W$
$x^{i \, \alpha \, -j} : {} \to V, W, V^{*}$
$x_{-\alpha \, -i \, j} : W^*, V^*, V \to {}$

我々の記法の $x^{i \, \alpha}_{j}$ は一番目の意味しか持ちません。このへんの混乱をうまく整理するために、アブラムスキーのネーム／コネームが使えます。

アブラムスキーは、x のネームを $\ulcorner x \urcorner$ と表しています。このとき使われている特殊な引用符は、コーナー引用符〈corner quotes〉、クワイン引用符〈Quine quotes〉、疑似引用符〈quasi-quotation〉などと呼ばれます。コネームは、コーナー引用符の上下逆の記号を使って $\llcorner x \lrcorner$ とします*5。

x のネーム $\ulcorner x \urcorner$
x のコネーム $\llcorner x \lrcorner$

x のネーム $\ulcorner x \urcorner$ と、x のコネーム $\llcorner x \lrcorner$ のプロファイル計算は次のようになります。

$\: x^{i\, \alpha}_{j} : V \to V, W \\ \mbox{-----------------------------------}\\ \: (\ulcorner x \urcorner)^{i\, \alpha\, -j} : {}\to V, W, V^*$

$\: x^{i\, \alpha}_{j} : V \to V, W \\ \mbox{-----------------------------------}\\ \: (\llcorner x \lrcorner)_{-\alpha\, -i\, j} : W^*, V^*, V \to {}$

ネーム化（ネームを作る操作）、半ネーム化（ネーム化の逆操作）、コネーム化、反コネーム化を絵でまとめておきます。ただし、反ネーム化、反コネーム化は一意的に決まるものではありません。

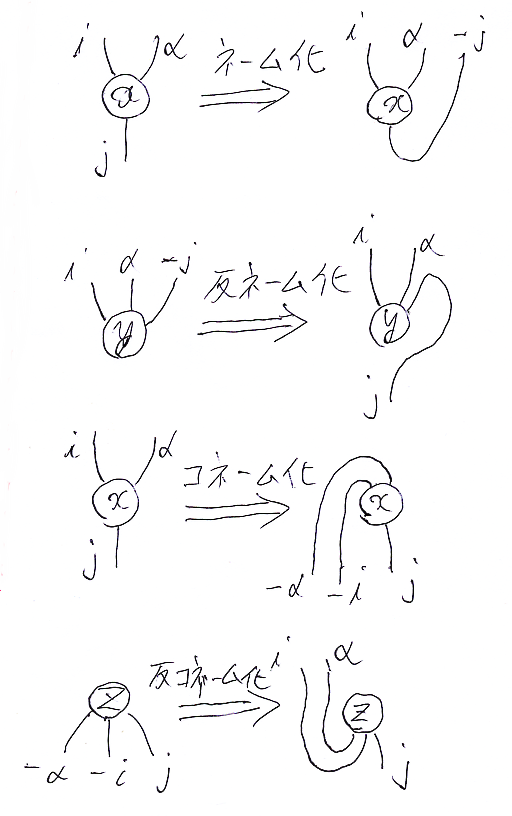
ネーム化／コネーム化、置換、三種の縮約を組み合わせると、伝統的テンソル計算より柔軟で精密なテンソル計算を展開できます。実際の利用法は、また機会を改めて。

インデックスとしての添字

今までの話は、添字をインデックスではなくてマーカーとみなすことからスタートしています。マーカーは、テンソルのプロファイルを注釈するものです。マーカーを付けても、テンソルの成分を取り出すことはできません、インデックスじゃないから。

伝統的テンソル計算が分かりにくい原因のひとつは、添字がほんとにインデックスなのか、マーカー（注釈）として使用しているだけなのかが曖昧で、どっちつかずに使用されていることがあるでしょう（どっちつかずでも計算はできるのですが）。今回、マーカーとしての添字の使用法を切り出して明確化しました。

テンソルに関する具体的な計算をするときは、基底を固定して、インデックスによる成分表示が必要です。それはマーカーの話ではありません。次は、インデックスとしての添字の使用法も明確化したいですね。

*1:アブラムスキー／クックが発明したわけではなくて、絵による記述は連綿と続く歴史を持ちます。興味があれば「バードトラック -- 群論的なファインマン図」をどうぞ。アブラムスキー／クック流の特徴は、ディラックのブラケット記法と相性がいい点でしょう。

*2:ここの説明は、若干「嘘も方便」のきらいがあります。R⁶ = R² $\otimes$ R³ としていますが、ほんとは R⁶ $\stackrel{\sim}{=}$ R² $\otimes$ R³ です。このへんのことをちゃんと扱うには、テンソル空間が持つ（ベクトル空間に付加された）構造を正確に定義する必要があります。n個のベクトル空間 V₁, ..., V_n、ベクトル空間 X、複線形写像 x:V₁× ... ×V_n→X を一緒にした ((V₁, ..., V_n), X, x) で、テンソル積としての普遍性を持つモノをテンソル空間と定義すればいいでしょう。こうすれば、R⁶ に複数の異なるテンソル空間構造が入ることをちゃんと示せます。