行列の圏のなかでモナドを探す - 檜山正幸のキマイラ飼育記 (はてなBlog)

「行列の係数を、ブール半環 B から取らないとウマくいかない」は間違いでした。僕が、別な事例と混同してました。係数は半環（一例：自然数半環）なら何でもいいです。

僕が混同していた「別の事例」とは何でしょうか？それは、この記事の表題である

行列の圏のなかで（モノイドではなくて）モナドを探す

事例でした。

行列の圏のなかには、モノイドが居ました（それが「行列の圏のなかでモノイドを探す」の主題）。モノイドの場合は、対象（自然数）n に対して、n を台〈underlying object〉とするモノイドは1個しかありませんが、モナドはもっとたくさんあります。

実は、行列の圏のなかのモナドは、有限集合上に載るプレ順序構造と同じなのです。行列の圏のなかでモナドを探すことは、有限集合上のプレ順序構造を探すことと同じです。このときの「行列の圏」はブール係数を使います。つまり、行列の係数〈成分 | 項目 | 要素〉は 0 か 1 です。

内容：

行列の係数半環
有向グラフとブール係数行列
プレ順序関係
行列の掛け算とブール順序
隣接行列によるプレ順序条件の表現
モナドの一般論へ

[追記]関連する内容の記事がありました。

順序集合や距離空間も実はモノイドだった

[/追記]

行列の係数半環

行列については説明しません（必要なら「はじめての圏論その第2歩：行列の圏」を見てください）。行列を構成している成分〈係数 | 項目 | 要素〉は、足し算と掛け算ができる必要があります。そうでないと、行列の足し算・掛け算が定義できませんから。

足し算と掛け算が定義されていて、よく知られている計算法則を満たす集合を半環〈semiring 〉と呼びます。小学校で最初に習う自然数（の全体）は典型的半環です。Sがなんらかの半環だとして、Sの要素を成分とする行列の全体を Mat[S] と書きます。

さて、集合 {0, 1} に次のように足し算・掛け算を定義しましょう。

+	0	1
0	0	1
1	1	1

×	0	1
0	0	0
1	0	1

これは半環になるので、ブール半環〈Boolean semiring〉と呼びます。足し算が論理ORに、掛け算が論理ANDに対応しています。ブール半環を太字で B と書きます。B は、単なる集合 {0, 1} ではなくて、足し算・掛け算も含めた構造を表します。

先程の約束により、ブール半環を係数とする行列の集合は Mat[B] です。n列m行（n行m列ではない！）のブール係数行列の集合は Mat[B](n, m) です。これは、圏のホムセット〈hom-set〉の記号で、n列m行の行列を n→m という射とみなしているのです（再び、必要なら「はじめての圏論その第2歩：行列の圏」を見てください）。

有向グラフとブール係数行列

グラフに関する基本概念の解説がこのブログ内にないかな？と探してみたら、カッとなって書いた記事（13年前）に簡潔な要約がありました。必要なら参照してください。

グラフ理論の基本概念とその誤用例 -- mixiがどうしたってぇ？ // グラフの定義もイロイロ

これから考えるグラフは有向グラフで、多重辺を許しません。つまり、単純有向グラフです。ループ〈自己ループ辺〉も孤立点も許します。一例を描けば：

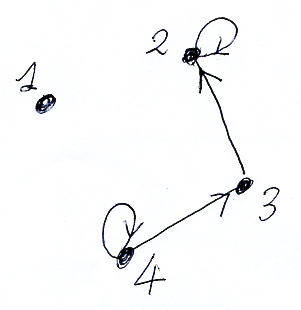
頂点には、1から通し番号を付けます。頂点数は有限です（辺も有限）。グラフ（正確には、頂点番号付き有限単純有向グラフ）が与えられたとき、それからブール係数行列を作ります。その作り方は：

グラフの頂点数を n として、行列のサイズは n×n （正方行列になる）。
頂点 i から頂点 j に向かう辺があるとき、i列j行成分を 1 にする。
それ以外の成分は 0 にする。

こうして作った行列を、グラフの隣接行列〈adjacency matrix〉といいます。先のグラフの隣接行列は次のようになります。

$\begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

頂点数は行列のサイズになり、辺の本数は 1 となる成分の個数になります。

「グラフから行列を作る」の逆方向に、任意の正方ブール係数行列が与えられると、対応するグラフ（正確には、頂点番号付き有限単純有向グラフ）を作れます。例えば、

$\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ \end{bmatrix}$

これは、4頂点の完全有向グラフを表します（描いてみましょうね）。また、

$\begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}$

これは、4頂点で辺がまったくない（4個の孤立頂点だけ）のグラフを表します。

プレ順序関係

集合S上の、なんらかの二項関係（中置関係記号として、'◁ 'を使います）があって、次を満たすとき、その二項関係をプレ順序関係〈pre-order relation〉と呼びます。

[反射律] 任意の x∈S に対して、x ◁ x
[推移律] 任意の x, y, z∈S に対して、x ◁ y かつ y ◁ z ならば x ◁ z

グラフ（正確には、頂点番号付き有限単純有向グラフ）があるとき、頂点 i から頂点 j に向かう辺があるなら i ◁ j と定義しましょう。先のグラフでは次のようです。

2 ◁ 2
3 ◁ 2
4 ◁ 3
4 ◁ 4

この例がプレ順序関係になっているかというと、なってません。が、自己ループ辺を付け加えて、間接的に結べる頂点は直接に（一本の辺で）結んでしまうと、プレ順序関係になります。

次の隣接行列で表現されるグラフは、我々の例に「自己ループ辺を付け加えて、間接的に結べる頂点は直接に結んで」作ったグラフです（描いてみましょうね）。

$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

圏論を知っているなら、プレ順序関係であるグラフがやせた圏〈thin category〉になることもわかるでしょう。

行列の掛け算とブール順序

行列の掛け算は普通のみんな知ってるアレです。通常、行列Aと行列Bの積は併置（単に並べる） BA で書きますが、中置演算子記号としてナカグロ〈ドット〉も使います。また、逆順の演算子記号としてセミコロンも使います。つまり、

BA = B・A = A;B

これは、行列の全体を圏と考えたときに、セミコロンが図式順結合記号、ナカグロが反図式順結合記号ということです。左右の入れ替えで混乱する人はトレーニングしましょう（「双対や随伴に強くなるためのトレーニング」参照）。

集合 {0, 1} に、順序 ≦ を次のように定義します。

0 ≦ 0
0 ≦ 1
1 ≦ 1

これは、順序関係（プレ順序より強い条件）になります。

ブール係数の行列 A, B に対して、A ≦ B は次のように定義します。関係記号 '≦' をオーバーロードしていることに注意してください。

A, B のすべての成分 A_{j i}, B_{j i} において、A_{j i} ≦ B_{j i} 。

この定義により、圏 Mat[B] のすべてのホムセット Mat[B](n, m) は順序集合（順序関係を備えた集合）になります。今定義した順序は、行列の足し算・掛け算と整合します。つまり、

A ≦ A' かつ B ≦ B' ならば A + A' ≦ B + B'
A ≦ A' かつ B ≦ B' ならば A;A' ≦ B;B'

隣接行列によるプレ順序条件の表現

n頂点のグラフ（くどいけど、頂点番号付き有限単純有向グラフ）があると、集合 {1, 2, ..., n} 上の二項関係（プレ順序関係かどうかは分からない）が定義できて、逆もしかりです。つまり、次の1：1対応があります。

n頂点のグラフ ←→ 集合 {1, 2, ..., n} 上の二項関係

また、グラフと隣接行列の対応もあるので、

n頂点のグラフ ←→ サイズ n×n のブール係数行列

グラフGが定義する二項関係を ◁_G 、グラフGが定義する隣接行列を A_G としましょう。すると、次の三者が1：1対応します。

G ←→ ◁_G ←→ A_G

勝手なグラフGを取ったとき、◁_G がプレ順序関係になることは保証されません。実際、我々の事例 G から作った ◁_G はプレ順序にはなりませんでした。「◁_G がプレ順序関係になる」ことを、Gの隣接行列 A_G によって表現しましょう。いきなり結果を言ってしまうと：

[反射律] I_n ≦ A_G
[推移律] A_G;A_G ≦ A_G

ここで、I_n はサイズが n×n の単位行列です。

上の不等式が反射律と推移律に対応することが分かりますか？成分で書くと分かりやすくなります。ただし、下付きの n（行列のサイズ）と下付きの G（グラフの名前）が、成分の添字〈インデックス〉とゴチャゴチャになるので、I_n を単に I、A_G を単に A とします。添字は、j が行番号、i が列番号です。僕は上下の添字が好きなんですが、今日は左右に配置します。

[反射律] $\mbox{For all}\: i, j,\:\; I_{j\,i} \le A_{j\,i}$
[推移律] $\mbox{For all}\: i, j,\:\; {\displaystyle \sum_{k=1}^n} A_{j\,k}\cdot A_{k\,i} \le A_{j\,i}$

行列成分は 0 か 1 でした。不等式の左辺が 0 のときはどうでもいいので、左辺が 1 のときだけを問題にすると：

[反射律] $\mbox{For all}\: i, j,\:\; I_{j\,i} = 1 \Rightarrow A_{j\,i} = 1$
[推移律] $\mbox{For all}\: i, j,\:\; {\displaystyle \sum_{k=1}^n} A_{j\,k}\cdot A_{k\,i} = 1 \Rightarrow A_{j\,i} = 1$

Iが単位行列だったことと、足し算する値にひとつでも1があれば和が1になることを思い出せば：

[反射律] $\mbox{For all}\: i,\:\; A_{i\,i} = 1$
[推移律] $\mbox{For all}\: i, j,\:\; {\displaystyle \exists k\in \{1, \cdots, n\}.}\; (A_{j\,k}\cdot A_{k\,i} = 1 \Rightarrow A_{j\,i} = 1)$

$\exists k\in \{1, \cdots, n\}.$ は、「カクカクシカジカの自然数 k （ただし、1 ≦ k ≦ n）が存在する」という意味です。

ここらでそろそろ、行列の言葉からグラフの言葉／二項関係の言葉に翻訳してみましょう。 $\mbox{For all}\: i,\:\; A_{i\,i} = 1$ は、「すべての頂点 i において、i から i に向かう辺がある」ことですから、i ◁ i が成立すること、確かに反射律です。

掛け算して 1 になるブール値は 1 と 1 しかないので、 $A_{j\,k}\cdot A_{k\,i} = 1$ は、 $A_{j\,k} = 1 \:\mbox{and}\: A_{k\,i} = 1$ あるいは逆順にして $A_{k\,i} = 1 \:\mbox{and}\: A_{j\,k} = 1$ です。よって、二番目はの条件は、適当な k に対して $A_{k\,i} = 1 \:\mbox{and}\: A_{j\,k} = 1 \Rightarrow A_{j\,i} = 1$ です。これをグラフの言葉で言えば、「頂点 i から頂点 k に向かう辺があり、頂点 k から頂点 j に向かう辺があるならば、頂点 i から頂点 j に向かう辺がある」です。さらに二項関係の言葉に翻訳すれば、「i ◁ k かつ k ◁ j ならば i ◁ k」となり、確かに推移律です。

モナドの一般論へ

有限集合上に二項関係が載っているとき、有限集合の要素に通し番号を付けてしまえば、{1, 2, ..., n} 上に二項関係があると思ってかまいせん。「二項関係 ←→ グラフ ←→ 行列」の1：1対応を利用すると、次が言えます。

有限集合上のプレ順序関係を探すことは、I_n ≦ A と A;A ≦ A を満たす行列 A を探すことと同じ。

「I_n ≦ A」が反射律、「A;A ≦ A」が推移律に対応するのですが、この2つの不等式は、とある圏の射と解釈できます。

I_n ≦ A は、圏 Mat[B](n, n) の射である。
A;A ≦ Aは、圏 Mat[B](n, n) の射である。

サイズ n×n の行列の集合 Mat[B](n, n) には順序関係 ≦ が備わっています。そう、順序集合ですね。順序集合はやせた圏とみなせます。だから、圏 Mat[B](n, n) と言ったのです。

Mat[B] は、全体として圏であるだけでなく、2つの対象（自然数）n, m を取ったとき、ホムセット Mat[B](n, m) も圏になっているのです。各 n, m ごとの圏（この場合、やせた圏）が、全体のなかに埋め込まれた構造です。このような構造を2-圏〈2-category〉といいます（2-圏の正確な定義は複雑です）。

特に、ホムセット Mat[B](n, n) は、結合（行列の掛け算）に関してモノイドになっています。なので、やせた圏としての構造（順序に基づく結合）に加えて、行列掛け算に基づくモノイド構造を持ちます。つまり、Mat[B](n, n) は（非可換な）モノイド圏なのです。

詳細はともかくとして、不等式「I_n ≦ A」と「A;A ≦ A」は、行列Aが、2-圏 Mat[B] 内のモナドになるための条件（の一部）なのです。このことを端的に言うと：

プレ順序関係に対応する隣接行列は、2-圏 Mat[B] 内のモナドである。

通常我々が「モナド」と呼んでいるものは、2-圏 CAT 内のモナドで、基礎圏をSetとするものです。通常のモナドと、今回のモナドを比較しておきましょう。

	通常のモナド	今回のモナド
環境となる2-圏	CAT	Mat[B]
台対象〈基礎対象〉	圏 Set	自然数 n
台射	関手 F:Set→Set	行列 A:n→n
モナド乗法	自然変換 μ::FF⇒F:Set→Set*	不等式 A;A≦A:n→n
モナド単位	自然変換 η::Id_Set⇒F:Set→Set	不等式 I_n≦A:n→n

関手の図式順結合を、諸般の事情から F*F と書いてますが、なんなら F;F でもかまいません。習慣（不等式には名前を付けない習慣とか）によるどうでもいい違いはありますが、十分に抽象化すれば、どちらも同じ構造（モナド）なのです。

行列の圏は思いのほか豊富な構造を備えていて、1-圏（通常の圏）としてモノイドをホストしている（内部に住まわせている）だけでなくて、2-圏としてモナドをホストしています。そして、この2-圏 Mat[B] 内に住むモナドは、有限プレ順序集合と対応しています。別な言い方をすると、有限なやせた圏は、2-圏 Mat[B] 内に住むモナドとして定義されるます -- この観点を（大幅に）一般化した話は以下の記事にあります。

モナド論をヒントに圏論をする（弱2-圏の割と詳しい説明付き）