はじめての圏論 第7歩：アミダの圏

第5歩、第6歩は、ちょっと難しかったかも知れませんね。ソフトウェアの話題なので、プログラムに関する経験がないと実感がわきにくいでしょう。第2歩も、行列計算の経験を仮定してますが、これは学校教育に入っているので、割と多くの人が予備知識を持っているように思えます。

いずれにしても、特定分野の予備知識を仮定して圏の実例を出すのは、最初の趣旨に反する気もするので、今回はまた（第1歩と同様に）予備知識なしの例を出すことにします。誰でも知っているアミダクジです。

アミダクジの全体は圏をなすのですが、これはなかなかに興味深い例で、わずかな変更や拡張で多方面に発展させることができます。例えば、ここ4半世紀ほどもホットな話題であり続け、ますます注目を浴びているブレイド（braid；組み紐）の圏は、アミダクジの圏と非常に近いものです。

内容：

1. 復習と注意
2. アミダ
3. アミダの結合
4. アミダの圏

• 全体目次

●復習と注意

圏論それ自体は抽象的な一般論なので、たいていの人（例外あり）にはツマラナイものだと思います。具体的な例／問題に適用／応用しないとね。しかし、適用／応用のためにはある程度の抽象論に耐える必要もあるわけで、これはどうもジレンマですな。

僕が言えることは、とにかく用語や記法に慣れてください、ってことです。次の用語、記法、コンベンション（習慣的な約束事）に慣れました？

1. 圏 C
2. 対象達の集合 |C| （Obj(C)という記法も使われる）
3. 射達の集合 C （圏全体の呼び名Cを流用、Morph(C)のように書くこともある）
4. 射fの域 dom(f)
5. 射fの余域 cod(f)
6. 対象aの恒等射 id_a
7. cod(f) = dom(g) のときにだけ定義される、結合（合成）と呼ばれる二項演算 f;g
8. dof(f) = a, cod(f) = b であることを表す矢印記法 f:a→b
9. dof(f) = a, cod(f) = b である射だけを集めたホムセット C(a, b)
10. 圏の結合法則 (f;g);h = f;(g;h)
11. 圏の単位法則 id_a;f = f;id_b = f （f:a→bのとき）

注意すべきは、分野や人により用語／記法が異なることです。既に注意したように、「fとgの、この順での結合」を f;g ではなくて g・f と書く人もたくさんいます。なかには、図式順記法に記号「・」（クロマルまたはシロマル）を使ってしまう人もいます。特定の記号を使わず、fg または gf と書くこともあります。

変数文字の使い方としては、対象をA, B, X, Yなどの英大文字、射はf, gなどの小文字を使う例が一番多いと思いますが、行列の圏では A:n→m と大文字／小文字の使い方が逆でした。僕自身は、対象も射も小文字を使うことが多いです（対象も射も大文字を使うケース／人もいます）。

その他、細かい“揺れ”を挙げだすとキリがありません（困った状況だけど、しょうがない）。用語／記法の差異にはとらわれないで、圏の概念そのものを把握するようにしてください。

●アミダ

下の図は、お馴染みのアミダクジです。アミダクジの図形を単にアミダと呼ぶことにしましょう。

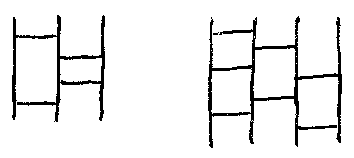
アミダの縦線には、左から順に 1, 2, 3, ... と番号を付けます。横棒にも上から順に 1, 2, 3, ... と番号を付けます。横棒の番号を曖昧さなく付けるために、同じ高さの横棒は禁止します。

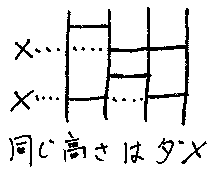
n番の縦線とn+1番の縦線を結ぶ横棒は「nから出る横棒」と呼びます。この用語を使って、アミダの一例（下図）を記述してみます。

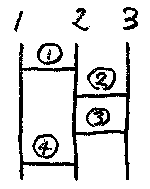
• 1番の横棒は、1から出る。
• 2番の横棒は、2から出る。
• 3番の横棒は、2から出る。
• 4番の横棒は、1から出る。

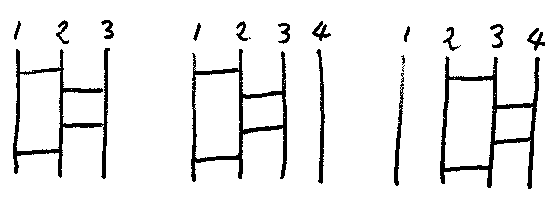
この記述を単なる整数の列 [1, 2, 2, 1]で表現します。この数列はアミダを完全に記述します。ただし、縦線の本数の違いを区別できない（下図）ので、数列に縦線の本数を添えて、[1, 2, 2, 1]₃のように書きましょう。次は、[1, 2, 2, 1]₃、[1, 2, 2, 1]₄、[2, 3, 3, 2]₄の図です。

●アミダの結合

図形としてのアミダを、[1, 2, 2, 1]₃のような数列で表示して、その数列表示が同じときにアミダも等しいとします。つまり、図形としての細かい差異は無視して、縦線と横棒の交差状況だけに注目して「等しさ」を定義するわけ。

一般に、「等しさ」の定義は困難なときがあり、圏を構成する際にも、対象や射の「等しさ」をうまく決めるために労力を使うときがあります。アミダは、数列表示にしてしまえば簡単に等しさが判定できますね。

アミダの縦線の数を幅、アミダの横棒の数を段数と呼び、それぞれ、width(A), rank(A) と記すことにします。例えば：

• width([1, 2, 2, 1]₃) = 3
• rank([1, 2, 2, 1]₃) = 4

AとBが同じ幅のアミダだとして、AとBの結合 A;Bを、Aのすぐ下にBを繋ぎ合わせたアミダだとします。A = [1, 2, 2, 1]₃、B = [2, 1, 2]₃とすると、A;B = [1, 2, 2, 1, 2, 1, 2]₃となります。

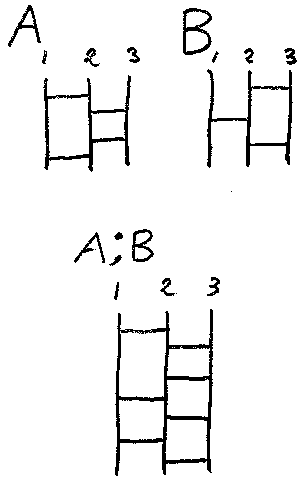
●アミダの圏

同じ幅のアミダどうしでないと結合は定義できません。これでも、ちゃんと圏になります。アミダの圏をAmidaとして、圏Amidaを定義しましょう。なお、Nは0を含む自然数の集合{0, 1, 2, 3, ...}です。

1. 対象の集合： |Amida| = N
2. 射の集合： Amida = すべてのアミダの集合
3. 域： dom(A) = width(A)
4. 余域： cod(A) = width(A)
5. 恒等射： id_n = []_n （横棒を持たないアミダ）
6. 結合： 前節で定義した演算

dom(A)とcod(A)が常に同じですが、別にこれは悪いことではありません。次の法則が成立していれば、リッパに圏のはずです。

1. cod(A) = dom(B) のときだけ A;B が定義できる。
2. dom(A;B) = dom(A)
3. cod(A;B) = cod(B)
4. dom(id_n) = n
5. cod(id_n) = n
6. (A;B);C = A;(B;C)
7. A:n→n のとき、id_n;A = A;id_n = A

最後の「A:n→n のとき」は、アミダの圏に特有な事情「dom(A) = cod(A)」を仮定してます。どの法則も、その意味に戻って考えれば、明らかに成立しています。

アミダの圏は、予備知識なしで紹介できるし、そこで使われている演算も単純なものです。が、みかけによらず深い構造を秘めています。面白い特性のいくつかを紹介できるといいんですが…（でも、先はどうなるかワカラン）