はじめての圏論第8歩：順序集合の埋め込み表現 - 檜山正幸のキマイラ飼育記 (はてなBlog)

新年の挨拶なんてのは省略。「はじめての圏論」シリーズいってみよう。

なんか、米田の補題（The Yoneda Lemma）について書きたくなった（単に気まぐれだけどね）。が、具体的に手でいじれる事例が欲しい。そこで、次のような方針にしました。

事例としてはやせた圏（thin categories）を使う。
“やせた圏＝プレ順序集合”に関して、米田の補題に相当する結果を先に示しておく。
この具体例を適宜参照しながら、一般的な米田の補題を説明する。

というわけで、今回はやせた圏（特に“とてもやせた圏＝順序集合”）の性質を多少詳しめに調べます。これは、米田の補題に向けての助走路となります。なお、やせた圏について「第3歩：極端な圏達」で紹介しているので、前もって読んでおくが吉。

内容：

記号と用語の復習
やせた圏のハッセ図
順序集合と上方集合／下方集合
典型的な順序集合
順序集合の表現
プレ順序集合の表現はどうなる？

全体目次

●記号と用語の復習

久しぶりの「はじめての圏論」なので、基本的な記号法／用語法を復習しておきます。

圏Cの対象（objects）の集合をObj(C)、または|C|と書く（主に|C|を使う）。
圏Cの射（morphisms）の集合をMorph(C)、または（不正確な記号法だが）単にCと書く（主にCを使う）。
圏の対象は a, bなどで示す（世間的には、大文字A, Bなどを使うほうが多い）。
圏の射は f, gなどで示す。
射fの域（domain）をdom(f)、余域（codomain）をcod(f)で示す。
対象aの恒等射（identity morphism）はid_aで示す（檜山は単にaと書くことが多いが、混乱しがちなので今回は“単にa”を使わない）。
射fと射gの、この順での結合（合成; composition）はf;gと書く（世間的には、g・fと書くことも多い）。
Cが圏、a, b∈|C|のとき、a, bのホムセット（hom-set）をHom_C(a, b)、またはC(a, b)と書く（主にC(a, b)を使う）。

矢印を使った記法 f:a→b は、dom(f) = a かつ cod(f) = b （つまり f∈C(a, b)）を意味します。

圏Tがやせた圏（thin category）であるとは、どんなa, b∈|T|に対しても、ホムセットT(a, b)がたかだか1個の射しか含まないことです。常に id_a∈T(a, a) ですが、どんなホムセットも2個以上の射を持てないので、T(a, a) = {id_a}（単元集合）。a≠bのときはT(a, b)=0（0は空集合）と定義するとTは離散圏（discrete category）になりますが、離散圏もやせた圏の仲間です（極限までやせた圏が離散圏）。

集合Aと、A上の二項関係≦が次を満たすとき、(A, ≦）をプレ順序集合（pre-ordered set）*1と呼びます。

[反射律] a≦a （すべてのa∈Aに関して）
[推移律] a≦b、b≦c ならば a≦c （すべてのa, b, c∈Aに関して）

やせた圏Tがあるとき、プレ順序集合(A, ≦）を次のように定義できます（「:=」と「:⇔」は、定義のための等号と論理的同値）。

A := |T|
a≦b :⇔ T(a, b)≠0

逆に、プレ順序集合(A, ≦）からやせた圏Tを次のようにして作れます。

|T| := A
T(a, b) = {[a, b]} :⇔ a≦b
T(a, b) = {} = 0 :⇔ a≦b ではない

ここで、[a, b]は、aからbへの唯一の射（それが存在するとき）を表します。今後も、[a, b]という記法は使います。

a≦b ⇔ 射[a, b]:a→b が存在する

特に、[a, a] = id_a。そして、[a, b];[b, c] = [a, c] という計算が出来ます。

●やせた圏のハッセ図

プレ順序集合(A, ≦)において、さらに次を満たすなら、それは順序集合（ordered set; partially ordered set; poset）となります。

[反対称律] a≦b、b≦a ならば a = b （すべてのa, b∈Aに関して）

順序集合(A, ≦)を効果的に図示する方法としてハッセ図（Hasse diagram）があります。Wikipeddia項目にきれいなハッセ図の例が載っています。ハッセ図を描くルールは：

Aのメンバーを点で表す。
a≦bのとき、aとbを線で結ぶ。
ただし、反射律、推移律から導かれる線は省略してよい（このルールにより、図を大幅に簡略化できる）。
線が交差するのはしょうがない。
a≦bのとき、bをaより上に描く。

プレ順序集合のときも同様な図を描けます。ただし、a≦b かつ b≦a であっても a=b とは限らないので、「a≦bのとき、bをaより上に描く」は適用できません*2。そこで、高さだけに頼らずに、点と点を結ぶ線に矢印を付けましょう。つまり、

a≦bのとき、a→bという矢線で結ぶ。

この方法で、プレ順序集合、つまりやせた圏を図示できます。下図の左側は（矢印を使った）ハッセ図の例です。右側は、ハッセ図では省略していた矢線（圏の射）をすべて描き足したものです。

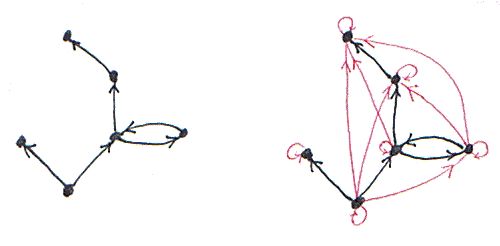
ハッセ図をたくさん描くと、やせた圏、ひいては圏論に慣れ親しむことができますよ。

●順序集合と上方集合／下方集合

順序集合(A, ≦)を考えます（プレ順序集合ではありませんよ）。Aの部分集合Xが下方集合（lower set）であるとは：

x∈X、y≦x ならば y∈X

つまり、xがXに属するなら、xより小さい元（メンバー）はすべてXに属するわけ。下方閉（lower closed; down closed）という形容詞のほうが感じが出るかもしれません。下側のほうにはズーッと広がっている、可能な限り下側に広がっている集合です。空集合とA自身も下方集合になります。

さて、SがAの勝手な部分集合として（S⊆A）、S↓を次のように定義します。

S↓ := {y∈A | 適当なx∈S があって、y≦x}

Sのメンバーにより上から抑えられている（S配下ともいうべきか）AのメンバーはすべてS↓に属します。雰囲気を図に描くと次のようになります。

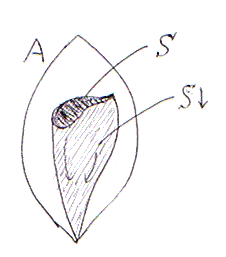
Sが何であってもS↓は下方集合になります。0↓ = 0 に注意してください。下方集合の定義に慣れるために、S↓が実際に下方集合であることを自分で示してみましょう。S↓は、Sを含む下方集合のなかで最少のものです（これも示せますか？チャレンジ！*3）。

Sが{a}のとき、{a}↓をa↓と略記します。定義から：

a↓ = {y∈A | y≦a }

一個人aの配下の者どもがa↓。a↓の雰囲気は次の図のようです。

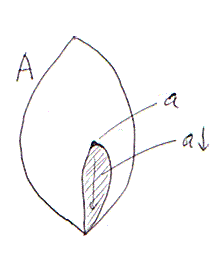
次も成立します。

S↓ = ∪_t∈S(t↓)

Sの各点tごとにtを頂点とする下方集合t↓を作って、それらすべての合併がSってことです。簡単な言い換えに過ぎませんから示してみましょう； yが∪_t∈S(t↓) に属するとは、適当なx∈Sがあって、y∈x↓ のことです。x↓ = {y∈A | y≦x } でしたから、y∈x↓ ⇔ y≦x 。つまり（同じ事を繰り返して言えば）、yが∪_t∈S(t↓) に属するとは、「適当なx∈Sがあって、y≦x」。直前の鉤括弧に入った命題はS↓の最初の定義そのものですね。よって、y∈∪_t∈S(t↓) ⇔ y∈S↓。これは集合の等しさを主張してます。

向きを逆にすると、上方集合（upper set）と、S↑、a↑も定義できます。

Xが上方集合 :⇔ x∈X、x≦y ならば y∈X
S↑ := {y∈A | 適当なx∈S があって、x≦y}
a↑ = {y∈A | a≦y }

●典型的な順序集合

あなたは“典型的な順序集合”と聞いて何を思い浮かべますか？自然数（0も含める）の全体{0, 1, 2, 3, ...}なんか典型的かもしれません。しかし、自然数全体は直線状に並んでいるので特殊です。“誰にもお馴染み”という点では“典型的”かもしれませんが、“一般的”ではありません。十分な一般性を持つ典型例は、集合Uのベキ集合（power set）Pow(U)です。Pow(U)は、集合Uのすべての部分集合からなる集合です。つまり、

X⊆U ⇔ X∈Pow(U)

定義から、0∈Pow(U)、U∈Pow(U)。順序関係としては、包含 X⊆Y を使います。(Pow(U), ⊆)が実際に順序集合であることは、次を示せば確認できます（ほぼ自明でしょう）。

[反射律] X⊆X （すべてのX∈Pow(U)に関して）
[推移律] X⊆Y、Y⊆Z ならば X⊆Z （すべてのX, Y, Z∈Pow(U)に関して）
[反対称律] X⊆Y、Y⊆X ならば X = Y （すべてのX, Y∈Pow(U)に関して）

Pow(U)には、Uの部分集合はなんでもかんでも入っているので、不必要に巨大になる傾向があります。

Aが順序集合のとき、つまり、A上に順序関係≦があるとき、Aの下方集合の全体をPow_↓(A)と書きましょう。Pow_↓(A)には、下方集合しか入ってないので、制限なしのPow(A)よりはずっと小さくてキリッとした感じの使いやすい順序集合になります。同様に、Aの上方集合の全体をPow^↑(A)と書きましょう。

Aを以下のようなダイヤモンド形順序集合{⊥, a, b, T}だとして、Pow(A)、Pow_↓(A)、Pow^↑(A)を、列挙により完全に書き下してみてください。ちょっと面倒ですよ。でも、やってみると実感が湧くはずです。

●順序集合の表現

(A, ≦)が与えられた順序集合、(K, ≦)が“典型的（かつ一般的）な順序集合”のとき、順序を保つ写像 R:A→K を表現（representation）と呼びます。順序を保つとは、「a≦b ならば R(a)≦R(b)」が成立することです。また、“表現”と呼んだココロは、「未知の順序集合Aのメンバーを、よくわかっていて取り扱いやすい順序集合Kのメンバーで表す／代用する」という感じです。

ここでは、“典型的な順序集合”として(Pow_↓(A), ⊆)を採用し、表現R:A → Pow_↓(A) を構成しましょう。Rの定義：

R(a) := a↓

つまりRは、Aのメンバーaに下方集合a↓を対応させるのです。Rが実際に表現になっていることを確認するには次を示します。

R(a)が下方集合であること（既に分かっている）。
a≦b ならば R(a)⊆R(b) であること（すぐに分かるでしょ）。

Aがダイヤモンド{⊥, a, b, T}のときに、R(⊥), R(a), R(b), R(T)を具体的に書いてみてくださいな。どう？ Aのメンバーが下方集合で“表現される”感じ、わかりますか。

さて、「a≦b ならば R(a)⊆R(b) 」だけじゃなくて、「R(a)⊆R(b) ならば a≦b」も言えます（確認せよ）。これからさらに、

R(a) = R(b) ならば a = b

が言えますね。これって、写像Rが単射（injective）なことだから、RによりAはPow_↓(A) に埋め込まれている（embedded）ことになります。つまり、Aは形を変えずにそのまま（「忠実に」とも言う）Pow_↓(A)のなかに入り込んでいるのです。

R'(a) := a↑ と定義したR'を使っても同様のことが言えますが、R'では順序関係が逆転します。

a≦b ならば R'(b)⊆R'(a)

R'を使うと、Aは逆さまになって（絵では上下をひっくり返す）Pow^↑(A)のなかに入り込みます。RもR'も表現ですが、Rは順序の向きがそのまま、R'では向きが逆転するので、Rは共変表現（covariant representation）、R'は反変表現（contravariant representation）と呼んで区別することもあります*4。

●プレ順序集合の表現はどうなる？

R(a) := a↓ で定義される R:A → Pow_↓(A) は、埋め込み表現（embedding）となります。同様な議論をAがプレ順序集合のときに適用できるでしょうか。つまり、順序集合のときと同様にRを定義したときに、Rが埋め込み表現となるでしょうか？今までの議論を注意深く読み返してみると、どこかで反対称律「a≦b、b≦a ならば a = b」が使われています。プレ順序集合では反対称律が使えないので、そのままでは破綻＜はたん＞します。しかし、うまく修正すると、埋め込み表現Rを構成できます。さて、どうしたらいいでしょうか？考えてみてください。

次回、実際に修正版の表現Rを構成してみます。

*1:前順序集合と呼ぶのが普通ですが、口頭では全順序集合と区別がつかないので「プレ」にしました。

*2:がんばれば、同じ高さの点を使って描けるかも知れないけど。

*3:示すべき命題を書き下すのが最初の困難かもしれない。

*4:RとR'は実は米田関手です。意味的には“米田表現”と呼びたいのですが、残念ながら「米田表現」は別な意味で使われているので使えません。「米田の表現関手」くらいが適切かもしれません。