「なぜ『光が影を作ること』と『主張の一部を再主張すること』が関係するのか;あるいは、デカルト圏入門」の課題17、18あたりの解答例を示しておきます。
まず↓。
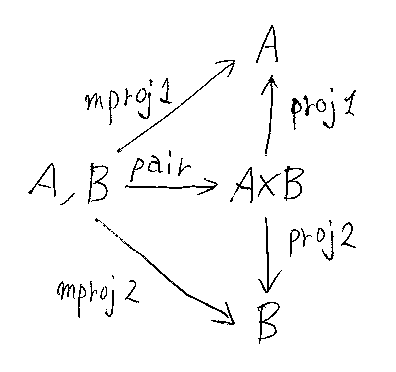
pair, proj1, proj2, mproj1, mproj2の関係はこれで尽きているでしょう。つまり:
- pair;proj1 = mproj1
- pair;proj2 = mproj2
「A, B」は、AとBの2引数を表し、A×Bは、タプルの1引数です。圏論風の記法を使いますが、総称型風の記法との翻訳は A×B ⇔ Pair<A, B>、C(A, B) ⇔ Func<A, B>。
もう1つ図。
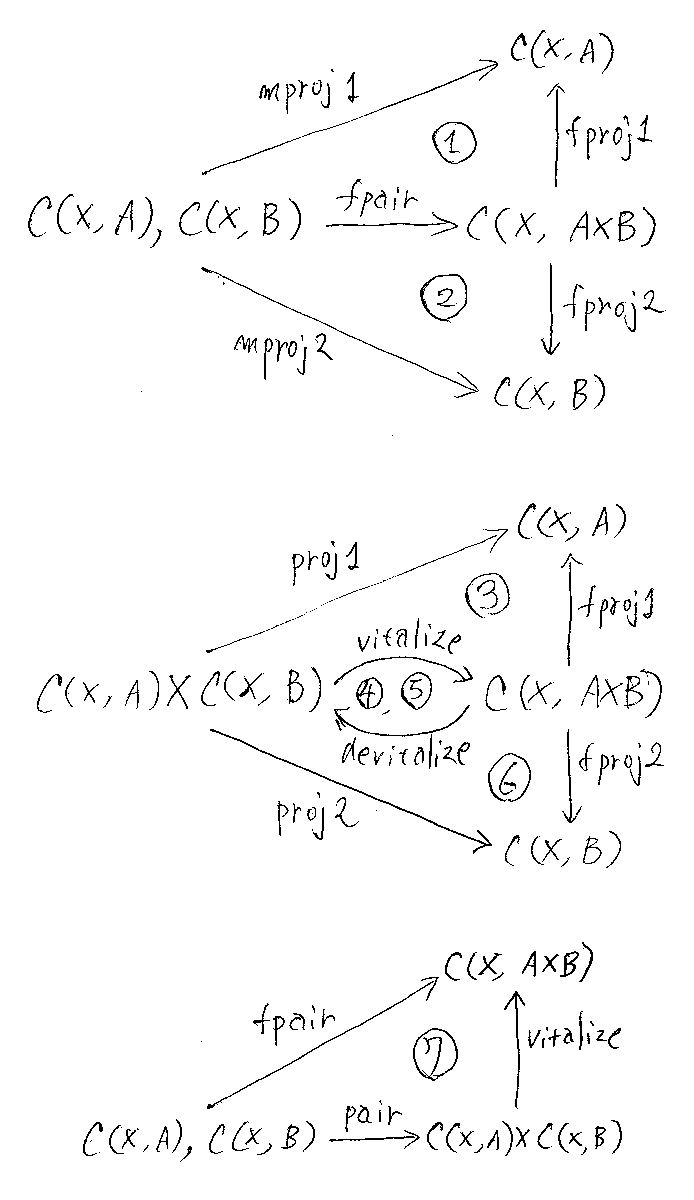
丸付き番号に対応する等式を書いておくと:
- fpair;fproj1 = mproj1
- fpair;fproj2 = mproj2
- vitalize;fproj1 = proj1
- vitalize;devitalize = id
- devitalize;vitalize = id
- vitalize;fproj2 = proj2
- pair;vitalize = fpair
圏論的な解釈としては、A×Bはともかく、A, B って何よ? ってことになりますが、たぶん、複圏(multicategory)や多圏(polycategory)を導入しないと意味付けできないでしょう。それと、ホムセットをもう一度対象と考えているので、C(-, -)は内部ホムになってます。