このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

ベックの法則と複合モナド

雑記／備忘

連休で疲れて、いまいち気力に欠けるんですけど … けど、モナドの話をします。2つのモナドを複合（合成）する、という話題。ある程度モナドに慣れている人向けかもしれない。

(F, μ, η), (F', μ', η') が同じ圏上の2つのモナド（μ, μ'はモナド乗法、η, η'はモナド単位）であるとき、関手としての結合F;F'（反図式順で書くならF'・F）が再びモナドになるかどうか？つまり、F;F'とうまく適合する乗法と単位を定義できるかどうか？ これについては、1960年代にベック（Jon Beck）が詳しく調べていて、事情がハッキリとわかっています*1。

で、実際に“複合モナドを構成可能な2つのモナド”の具体例を出します。この実例に対してベックの法則*2や、複合の方法を紹介します。しかし、複合がうまくいく内的なメカニズムまで説明できそうにありません。グチャグチャした複雑な等式を天下りに出すことになりそうなので、先に言い訳と種明かしをしておきます。

  • 個々の等式（ベックの法則、複合モナドの定義など）の意味は、具体例で考えれば難しくはありません。それらを確認することも、手間さえかければできることです。
  • 複合モナドの構成法は、ある抽象レベルで見ると、2つのモノイド(M, m, e)と(M', m', e')から、M×M'を台（underlying set, carrier）とするモノイド（積モノイド）を構成する方法とまったく同じです。
  • ベックの法則や複合モナドの定義などは、ある抽象レベルにおける絵（pictorial/graphical/diagrammatic representation）を持ちます。これは簡単な絵です。後で挙げる等式群は、これらの絵を見ながらテキスト形式（通常の記号表現）へと書き下したものです。

途中は読み流しでけっこう。最後の節にアヤシゲな妄想、ここでなんだかナゾな雰囲気を味わってくださいな。

内容：

ListモナドとEnumモナド

モナドを次のスタイルで表現します。詳細は「モナドの定義とか」を参照のこと。

  1. 任意のデータ型Xから新しいデータ型F<X>を生み出す型構成子F（実体は、集合圏上の自己関手）。
  2. Fに付随するマップ関数mapF:(X→Y)→(F<X>→F<Y>)。mapFは2引数関数mapF(f, t)（f:X→Y, t∈F<X>）の形で使う。
  3. Fに付随する平坦化関数flattenF:F<F<X>>→F<X>。
  4. Fに付随する単位関数unitF:X→F<X>。

まず、Listはお馴染みのリスト・モナドだとします。下付き添字や山形括弧がうっとうしい*3ので、次の約束をしましょう。

  • mapList, flattenList, unitListの代わりに、l_map, l_flatten, l_unitを使う。
  • List<X>の代わりに、山形括弧なしの List X を使う。

もうひとつ、Enumというモナドを登場させます。Enum Xは、型Xに対する列挙型ですが、プログラミング言語の列挙型とは少し異なります。Enum X は、単に“Xの有限部分集合の型”です。例えば、X = Integer なら、{0}や{1, -3, 7}などがEnum Integerに属するデータです。列挙要素の順番は考えず、列挙要素に名前を付けることもしません*4。Xが集合として有限なら、Enum X も有限です。例えば：

  • Enum Boolean = Enum {true, false} = {{}, {true}, {false}, {true, false}}

Listのときと同様に、mapEnum, flattenEnum, unitEnumの代わりに、e_map, e_flatten, e_unitを使います。定義は書き下しませんが、いくつか具体例を出せばわかるでしょ：

  1. e_map(add1, {1, -3, 7}) = {add1(1), add1(-3), add1(7)} = {2, -2, 8}
  2. e_flatten({{0}, {1, -3, 7}, {1, 2}}) = {0, 1, -3, 7, 2}
  3. e_unit(0) = {0}

e_map(f, A)は、関数fによる集合Aの像f(A)、そしてe_flattenは、いくつかの集合に対して、それらの合併を作る操作であることに注意してください。圏論の用語法で言えば、Enumは有限ベキ集合モナド（finite powerset monad）です。

combinations関数

Xが型だとして、List Enum X は、「Xの値を列挙したもの（有限部分集合）のリスト」の型です。例えば、X = Integer なら、[{0}, {1, -3, 7}, {1, 2}] はList Enum Integer に属するデータです。ここで、[a, b, ...] はリストを表すとします。

さて、combinations : List Enum X → Enum List X という関数を定義しましょう。まずは例から：

  1. combinations([{0}, {1, -3, 7}, {1, 2}]) = {[0, 1, 1], [0, -3, 1], [0, 7, 1], [0, 1, 2], [0, -3, 2], [0, 7, 2]}
  2. combinations([{0}, {1, 2}]) = {[0, 1], [0, 2]}
  3. combinations([{0}, {1}, {2}]) = {[0, 1, 2]}
  4. combinations([{0}, {}, {2}]) = {}
  5. combinations([{1, 2}]) = {[1], [2]}
  6. combinations([]) = {[]}

combinationsの働き、わかりますか？ 名前の通り、「すべての可能な組み合わせを作る」関数です。combinations([A1, ..., An])を求めるには、[a1, ..., an]（a1∈A1, ..., an∈An）の形のリストを全部列挙します。

集合Aの個数を #(A)（cardinal number of A）と書くことにすると、

  • #(combinations([A1, ..., An])) = #(A1)×...×#(An)

が成立します。“組み合わせの数”ですから掛け算ですね。これはまた、combinationsが、いくつかの集合をすべて、直積として掛け合わせる演算であることも示唆します（直積については、「タプルと直積」参照）。実際、combinations([A1, ..., An]) = A1×...×An（“×”は直積、全体としてリストの集合）です。

ベックの法則

Listモナド（l_map, l_flatten, l_unit）とEnumモナド（e_map, e_flatten, e_unit）、それとcombinations関数、これで素材は揃いました。「なにをイキナリ!?」と困惑と非難を引き起こしそうですが、ベックの法則と呼ばれる等式を以下に並べます。引数変数がlleなら"list of list of enumeration"の略、leeなら"list of enumeration of enumeration"の略です。

  • 等式1 combinations(l_unit(enu)) = e_map(l_unit, enu)
  • 等式2 combinations(l_map(e_unit, lis)) = e_unit(lis)
  • 等式3 e_flatten(e_map(combinations, combinations(lee)) = combinations(l_map(e_flatten, lee))
  • 等式4 e_map(l_flatten, combinations(l_map(combinations, lle))) = combinations(l_flatten(lle))

唐突でしょうが、ひとつひとつの等式はそれほど不思議ではないと思います。例えば、等式3をインフォーマルに示してみましょう。「なんだかウジャウジャで耐えられん」と思ったらスキップして、次の節に進んでください。

leeを [{A1, ..., Aa}, ..., {Z1, ..., Zz}] のように書いておきます。小文字のa, ..., zは（0かも知れない）自然数です。このリストの長さはNとします、「AからZだから、長さ26」ではありません :-)

  1. combinations(lee)により、[Ai1, ..., ZiN] のようなリストが列挙される。ここで、1≦i1≦a, ..., 1≦iN≦z。
  2. e_map(combinations, -)の適用により、combinations([Ai1, ..., ZiN])が、[x1, ..., xN]（x1∈Ai1, ..., xN∈ZiN）のようなリストの集まりを生み出す。この時点で、値は「リストの集まり（列挙）の集まり（列挙）」である。
  3. e_flattenを適用することにより、結局、「第1項目をA1, ..., Aaのどれかから選び、… 第N項目をZ1, ..., Zzのどれかから選んだリストの集まり」が生じる。
  4. 値の集合は、(A1∪...∪Aa)× ... ×(Z1∪...∪Zz) である。

右辺のほうは：

  1. l_map(e_flatten, -)の適用により、各項目が A1∪...∪Aa, ..., Z1∪...∪Zz であるリストができる。
  2. combinationsを適用すると、集合としては、(A1∪...∪Aa)× ... ×(Z1∪...∪Zz) となる。

これで、右辺と左辺が同じ値（値は集合）だとわかります。その他の等式も確認してみてください。具体的で単純な例を手計算したり、動くプログラムを作って実験するのもよいと思います。

複合モナドEnumOfList

さてところで、ベックの法則はいったいどこから来て、何の役に立つのでしょうか？ この法則は、実は複合モナドの構成に由来します。ベックの法則が、2つのモナドが複合可能である条件を与え、ベックの法則を利用して複合モナドを実際に構成できるのです。という次第で、ListとEnumの複合を考えましょう。

Enum List X を EnumOfList X と書いて、EnumOfListを新しい型構成子とみなしましょう。型構成子だけではモナドにはなりません。型構成子EnumOfListと連動・協調したmap関数、flatten関数、unit関数が必要です。ネタバラシしてしまうと、EnumOfListに対応するmap, flatten, unitは次のように定義できます。

  • el_map(f, el) := e_map(l_map(f), el) （ここでは、l_mapを1引数で使う）
  • el_unit(x) := e_unit(l_unit(x))
  • el_flatten(elel) := e_flatten(l_flatten(e_map(combinations, elel)))
    el_flatten(elel) := e_flatten(e_map(e_map(l_flatten), e_map(combinations, elel)))

[追記][1..100]>>=pen さんのご指摘により、すぐ上の定義式を修正しました。詳細は、「総称高階関数計算の練習：積モナドの乗法を書き下す」と「総称高階関数計算の練習：解答編」を参照。[/追記]

これらが実際にモナドであるためには、次のモナド法則を満たす必要があります（「モナドの定義とか」の「代数スタイルの定義」を参照）。

  1. el_flatten(el_unit(el)) = el
  2. el_flatten(el_map(el_unit, el)) = el
  3. el_flatten(el_flatten(elel)) = el_flatten(el_map(el_flatten, elel))

el_* の定義に従い律気に確認することができます。しかし、簡単そうな一番目の等式でも、el_* の定義を代入すると次の形になります。

  • e_flatten(l_flatten(e_map(combinations, e_unit(l_unit(el))))) = el

うーん、ゲンナリするなー。

絵を使えば劇的に簡単になるのだ

「ListモナドとEnumモナド、そしてcombinations関数のあいだにベックの法則が成立している」こと、「ベックの法則を仮定すれば、EnumOfListとel_*関数達がモナド法則を満たす」ことは、力ずく計算（brute-force calculation）で示すことができます。しかし、その計算の背後に何があるかは見えにくいでしょう。

そもそも、ベックの法則やモナド法則を通常の等式として書いたものは、記憶にも計算にも好都合とは言えません。そこで、図（picture, diagram）による表現と計算（図形の変形操作）の出番です。図（絵）の描き方の基本は『ストリング図による複合モナドの計算 (1)』に書いておきました。

『ストリング図による複合モナドの計算 (1)』の「はじめに」で、

ストリング図を使うと、計算が劇的に簡単になることがわかった。

と述べたのですが、実際にその効果は“劇的”で、記号と等式による煩雑な計算をバイパスできます。詳細はともかくとして、実際の絵を眺めてもらいましょう。ベックの法則（4つの等式）に対応する絵は以下のとおりです。LはList、EはEnum、IはId（恒等関手）の略記です。小さな三角がモナド単位（unit関数）、小さな丸がモナド乗法（flatten関数）、そして線の交差がcombinations関数に相当します。

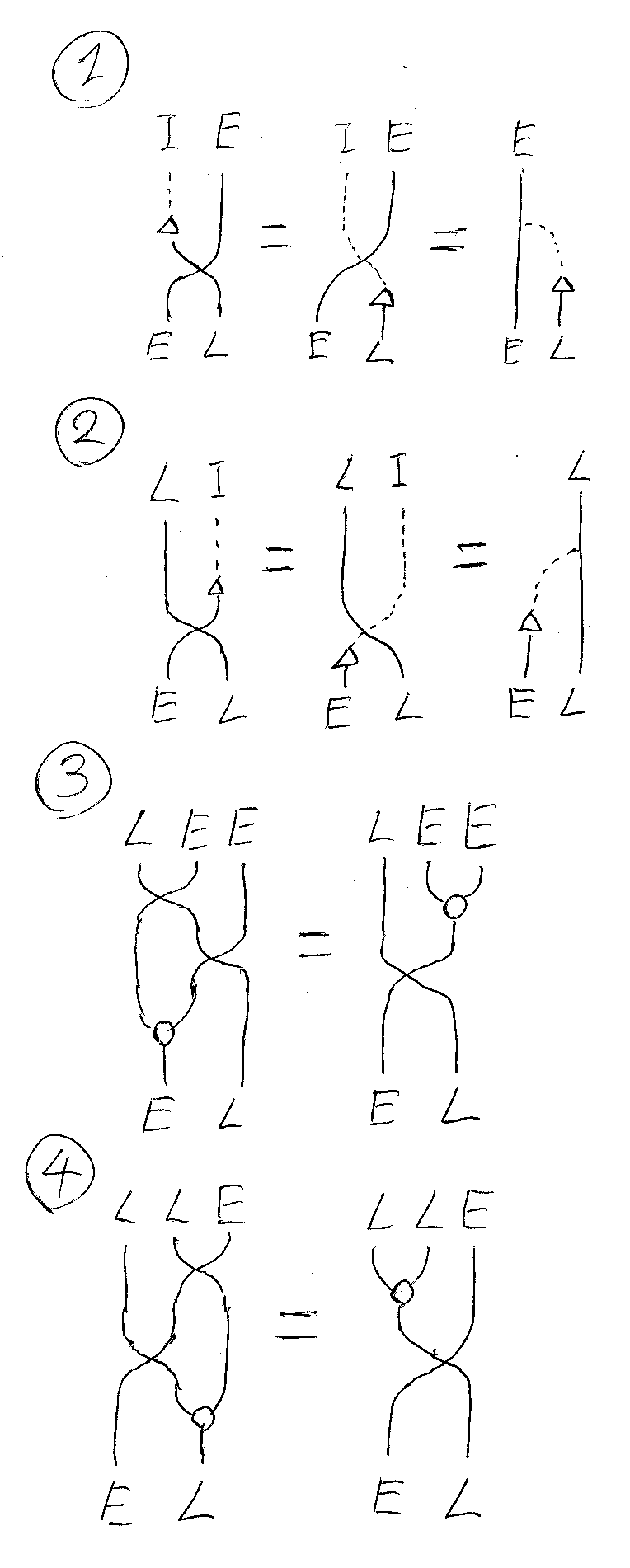
『ストリング図による複合モナドの計算 (1)』に曰く：

ストリング図を使って、複合モナドを実際に構成してみる（実際の構成は、この記事の続編である(2)になる）。

いまだに(2)は書いてないし、すっかり忘れてるわけで、困ったもんですが、いずれ説明の機会もあるでしょう。

すべり台が法則の起源かもしれない

絵による表現から通常の記号表現（テキスト形式）に翻訳する規則は存在します。その意味で2種の表現は同値ですし、記号表現のほうが有利な場面も確かにあります。しかし、絵の簡潔さとテキストの煩雑さを比べると、「現在の記号表現は、モナドのような高水準の事態や現象を記述するには不向きなのではないか」と疑りたくなります。

さらにファンタスティックな（あるいはアヤシイ）もの言いをすれば、絵による表現は記憶や計算を助ける補助的道具なのではなくて、事態／現象の真の姿により近いのではないか、と思えます。もし、“真の姿”が単純明快だとすれば、より単純明快に見えることは、その描写が“真の姿”に肉薄している、ってことじゃないでしょうか。

ところで、経験則なのですが、先に挙げた図式のように「左の図 = 右の図」という“図等式”があると、その背後には、図形の連続変形があるようです。ベックの法則・等式4に関して絵を描いてみましょう。

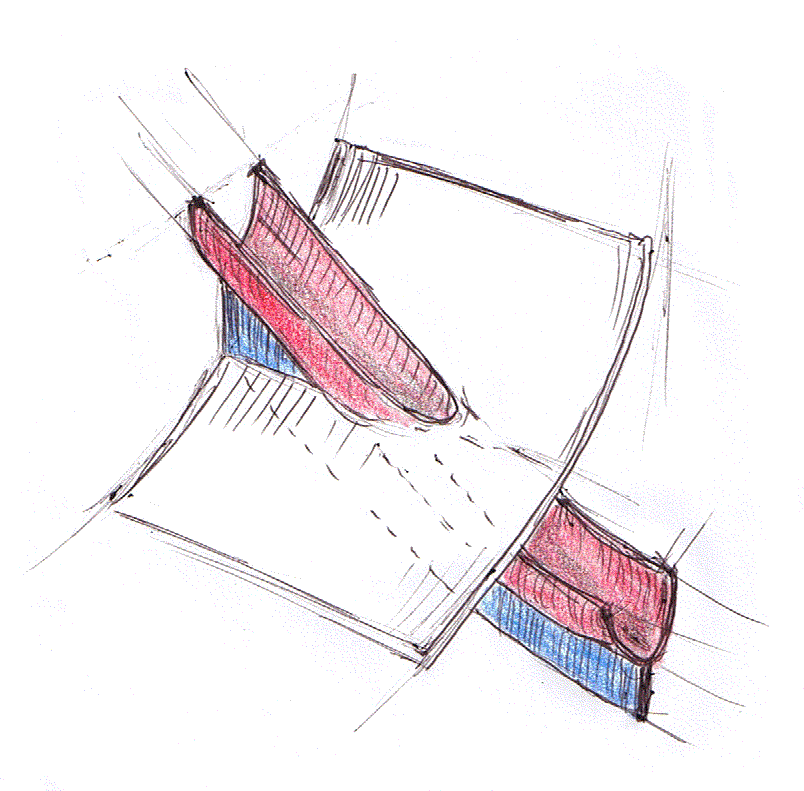
チューブを半分に切り裂いたような形のすべり台（赤）が、斜めの壁を突き抜けている絵です。青い部分は、すべり台に垂直に取り付けられた面です。この絵はだいたいの雰囲気を伝えるもので正確ではありませんが、このテの図形を二箇所で輪切りにした断面（スナップショット）を並べると、法則を記述する“図等式”になります。

とある世界に在るすべり台が（そのすべり台は、さらに別な世界に在る別な図形の影に過ぎないようですが）、ベックの法則のような一見複雑な法則の起源であるように思えるのですが、ファンタスティックに過ぎるかしら？

*1:マックレーンのthe bookの出版が1971年であることから分かるように、圏論の基本的な結果は50年代／60年代、つまり半世紀前に既に出揃っていたんです。

*2:通常、ベックの分配法則と呼ばれますが、「分配」にこだわらないほうがいいと思うので、単にベックの法則と呼ぶことにします。

*3:暗黙の（あるいは自動的）型付けを明示すると、mapF<X, Y>のように、さらに型パラメータが増えます。これではタマランよねー。

*4:Enum Xは、“Xの（有限）部分集合型”と呼ぶのが正確でしょう。が、“列挙型”のほうが馴染みやすい気がします。