「1+1ができない子と線形論理」で、リソースに敏感な態度を紹介したのですけど、リソースに敏感になるためには、リソースの勘定ができないといけません。ごく普通の計算式のなかに、どのくらい計算リソースが含まれているか勘定する練習をしてみましょう。
ここでは、計算リソースとして次の6種類を考えます。
- 可算器 -- 2つの入力の足し算を実行して出力する。
- 減算器 -- 2つの入力の引き算を実行して出力する。
- 複製器 -- 1つの入力をコピーして2つの出力に出す。
- 交差器 -- 2つの入力の順番を入れ替えて2つの出力に出す。
- 放電器 -- 1つの入力を安全に捨て去る。
- 定数発生器 -- 何の入力もなしで、ある定数を出力に出す。
それぞれのリソースを次のようなアイコン(絵記号)で示すことにします。
![]()
これらの基本素子をワイヤーで繋いで、目的の計算を実行する回路を組み上げたとき、基本素子を何個使ったかで、その回路(が実現する機能)のリソース消費量を計れるでしょう。例として、入力が3つ(x1, x2, x3)、出力が3つ(y1, y2, y3)の回路を考えます。
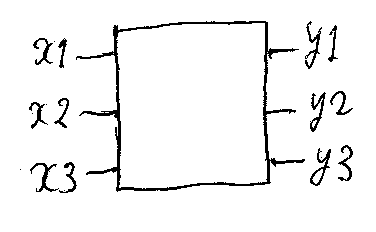
次の式で表現される機能を実現する回路は、どのくらいのリソースを使用するでしょうか?
- y1 = x1 + x2
- y2 = x2 - x1
- y3 = 1
考えてみてください。
回路の絵はこんな感じです→回路の例
意外とリソース使っているでしょ(合計8個)。普通、複製器、交差器、放電器、定数発生器なんて意識してませんからね。そんな、意識してなかったリソースにも目配せすることがリソースに敏感な態度なわけね。
練習問題です。次の式で表現される機能のリソース使用量を計ってください。
- y1 = x1
- y2 = x2
- y3 = x3
- y1 = x2
- y2 = x1
- y3 = x3
- y1 = x3
- y2 = x1
- y3 = x2
- y1 = x3
- y2 = 5
- y3 = x1
- y1 = x1 + x2
- y2 = x1 - x2
- y3 = x3
※ 事前に式を簡略化しないでください。
- y1 = x1 + x2
- y2 = (x1 + x2) - (x2 + x3)
- y3 = x2 + x3
- y1 = x2 + 5
- y2 = 5 - x3
- y3 = x3 + 5
- y1 = x3 - x2
- y2 = x1 - x3
- y3 = x2 - x1