http://d.hatena.ne.jp/m-hiyama/20100713#c :
ティッツの50年前の観察から30年近く誰も顧みなかったことが90年代から、特に21世紀に入って火がついたみたいです。でも、ガウスのようなウルトラ天才は200年前にある程度は見越していた気配があります。
てなことを、 F1の歴史が書いてある論文で一昨日知りました。
> F1はリーマン予想絡みでもホットだとか?
その歴史付き論文を読んで、リーマン予想絡みであることと、多くの日本人が本質的に貢献していることを知りました。
今日も、いわゆる一元体F1(エフイチ)の話です。上記コメント内の「F1の歴史が書いてある論文」とは次です。
- Title: Mapping F1-land: An overview of geometries over the field with one elementa
- Authors: Javier Lo'pez Pen~a, Oliver Lorscheid
- URL: http://arxiv.org/abs/0909.0069
- Pages: 21 pages
題名の"Mapping F1-land"は、エフイチ大陸の地図を作ろうといった意味だと思います。以下、この論文を「エフイチ大陸の地図」として引用します。
僕がエフイチについて知ったのは、たまたまコンヌ/コンサニ論文を目にしたからです。
- Title: Characteristic 1, entropy and the absolute point
- Authors: Alain Connes and Caterina Consani
- URL: http://www.alainconnes.org/docs/Jamifine.pdf
- Pages: 66 pages
コンヌ/コンサニ論文を(読めるところだけ)拾い読みしているうちに、F1の全体像を知りたくなったのですが、ペーニャ/ロアシャイド*1の「エフイチ大陸の地図」はそんな目的にはピッタリです。F1研究の歴史と現状が手際良くまとまっています。
「エフイチ大陸の地図」の、F1の歴史の記述を読んで「ヘーッ、そうだったのぉ」と少し驚いたことが2つあります。
- リーマン予想と密接に関係する。
- 日本人の貢献が非常に大きい。
リーマン予想に関してはサッパリわかりません。F1上でゼータ関数を定義して計算することが、リーマン予想解決につながるような、なんかそんなことらしい。ともあれ、動機がリーマン予想なら、数論が盛んな日本の研究者がたくさん登場するのは必然なのかもしれません。
以下に、「エフイチ大陸の地図」から抜粋して(つまり孫引き、受け売りで)、F1の歴史に登場する日本人を紹介します。人名と年代だけです。論文のリストは「エフイチ大陸の地図」の参考文献にあります。
発端は、1956年にティッツ(Jacques Tits)が「一元体(field with one element)があったらいいな」と言い出したことです。バエズのエッセイ http://math.ucr.edu/home/baez/week259.html の冒頭を引用すると:
"field with one element" - even though it doesn't exist. It's a mathematical phantom.
あればいいけど、そんなものは存在しない、幻なのです。
一方、http://arxiv.org/abs/math/0407093 のヘンリー・コーン(Henry Cohn)の言葉:
There is no field with only one element, yet there is a well defined notion of what projective geometry over such a field means.
一元体はないけど、一元体上の射影幾何はちゃんと定義できる、と -- ナンジャソリャ? わけが分からんので、一元体がすぐに注目を集めることはなかったようです。
1991年になって、デニンガー(Christoph Deninger)が代数幾何に一元体を使い始め、同じ時期に黒川(黒川信重; Nobishige Kurokawa)も一元体上でゼータ関数の定義と計算をしてます。マニン(Yuri Manin)がデニンガー/黒川に注目し、1995年に*2解説と紹介をしてから、ある程度は知られるようになったみたいですね、一元体。2005年には、黒川/落合(落合啓之; Hiroyuki Ochiai)/若山(若山正人; Masato Wakayama)によりF1の幾何とゼータ関数に関する論文がまとめられました。
現在、一番良く使われているF1スキームの定義はデイトマー(Anton Deitmar)によるもの(2005年)らしいです。その定義は、1994年の加藤(加藤和也; Kazuya Kato)のアイディアに基づいています。デイトマーが定義したスペクトルを加藤スペクトル(Kato spectrum)と呼ぶ人もいます。
マニンは、2008年になってF1上の解析幾何なるものを提示します。ここで解析幾何は、座標幾何の意味じゃなくて、解析関数(正則関数)の概念を使う幾何でしょう、たぶん。ウーン、一元体の解析関数、想像もできない。それはともかく、マニンの解析幾何は葉廣(葉廣和夫; Kazuo Habiro)の方法の拡張なんだそうです。
ついでに、「エフイチ大陸の地図」からほんとの“地図”を引用しましょう。
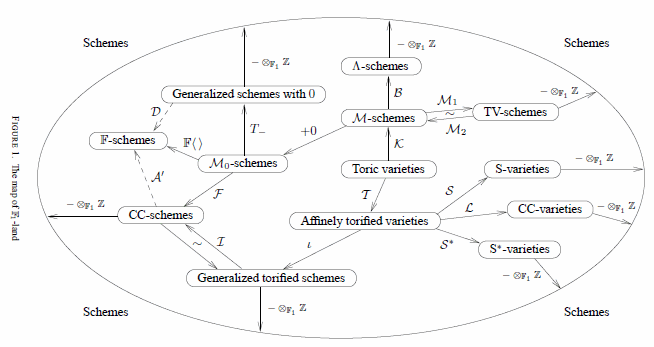
ごく一部だけはかすかに分かるので、地図の説明をいずれまた。