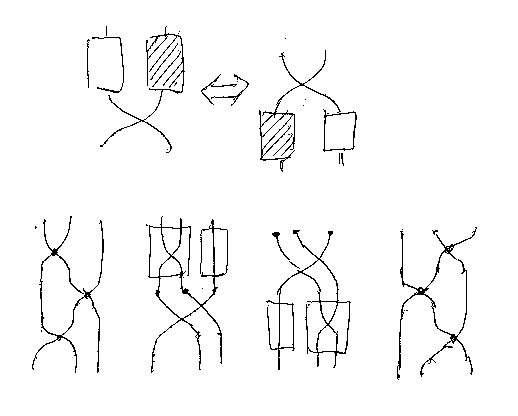先週末のエントリー「圏のクリーネスター構成 -- エフイチに触発されて」において、次の図を出しました。
これは、ヤン・バクスター方程式(Yang-Baxter equation)です。ライデマイスター移動III(Reidemeister move III)ともいいます。もともとはブレイドに関連する関係式なので、手前と奥が区別されていますが、アミダのように単なる交差だけを問題にするなら、手前と奥の区別は不要です。このエントリーでは、交差(対称、置換、ツイスト、フリップ、スワップなど色々な呼び名があります)だけを問題にします。
「圏のクリーネスター構成 -- エフイチに触発されて」と同じ記法を使うことにしますが、モノイド積は「+」、モノイド単位は「0」で表すことにします。(C, +, 0)がモノイド圏のとき、σa,b:a+b→b+a が対称を与える射の族だとします。σはヤン・バクスター方程式を満たす必要があります。ヤン・バクスター方程式は絵で描くほうが断然分かりやすいですが、記号テキストを使った表現は次です。
- [σa,b+c];[b+σa,c];[σb,c+a] = [a+σb,c];[σa,c+b];[c+σa,b]
ヤン・バクスター方程式は基本的な関係ですが、より基本的な性質から導出できます。その性質とは:
- σが自然変換であること
- σが指数法則を満たすこと
σが自然変換であること
モノイド積+は、C×C→C という二項関手(双関手)です。Tをペア(二項タプル)の順番を入れ替える関手とします; T:C×C→C×C。すると、σは、関手+からT;+ への自然変換です。と言っても分かりにくいので順番に説明します。T;+ を +' と略記して、+ と +' を具体的に書き下します。中置演算子を前置の関手記号としても使います。
- +[(a, b)] = a+b
- +[(f, g):(a, b)→(x, y)] = (f+g:a+b→x+y)
- +'[(a, b)] = b+a
- +'[(f, g):(a, b)→(x, y)] = (g+f:b+a→y+x)
一般に、α::F⇒G:D→E が自然変換である条件(自然性)は、次の可換図式となります。
F(a)- F(f) →F(b)
| |
α_a α_b
| |
v v
G(a)- G(f) →G(b)
σ::+⇒+':C×C→C に関して書き下すと:
+[(a, b)]- +[(f, g)] →+[(x, y)]
| |
σ_(a,b) σ_(x,y)
| |
v v
+'[(a, b)]-+'[(f, g)]→+'[(x, y)]
もっと分かりやすい記法を使うと:
a+b - f+g → x+y
| |
σ_(a,b) σ_(x,y)
| |
v v
b+a - g+f → y+x
等式で書けば次のようです。
- (f+g);σx,y = σa+b;(g+f)
絵で描くとずっと鮮明です。
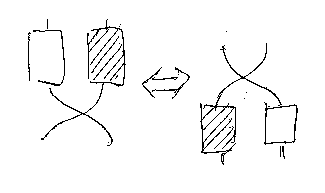
σが指数法則を満たすこと
指数法則と言ったのは次の等式です。[追記]次の等式(同型)を文字通り解釈すると変ですね。下にある絵のほうを信じてください。x+yによる作用がxによる作用とyによる作用の繰り返しと同じって点では指数法則っぽいです。[/追記]
- σa,x+y = σa,x;σa,y; (間違っている)
- σa,0 = a
- σa+b,x = σb,x;σa,x; (間違っている)
- σ0,x = x
これはアクション性とかバニッシング法則と呼ぶこともあります。主張している内容は次の絵と同じことです。
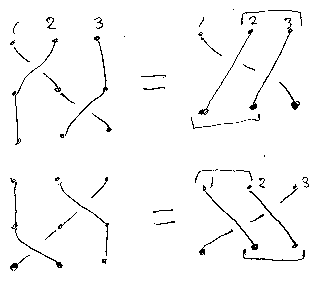
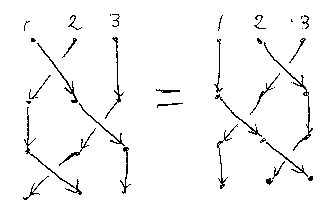
ヤン・バクスター方程式の導出
次の絵の通り(絵の上段は自然性を再掲)。