アクセス数に絶対に寄与しないエントリー、行ってみましょう。僕のこのテの記事は目で読むだけでは分かりにくいと思うので、絵を描いたり計算したりと、手も動かしてください -- と、そんな作業を要求することが敬遠される理由でしょうがね(苦笑)。
テンソル強度(tensorial strength)関連の絵算が楽しいので説明しようと思ってるんですが、テンソル強度自体の定義や実例なしで計算方法を示しても面食らっちゃいますよね。で、実例を挙げます。今日は典型的な例を2つ。もっと面白い例を後日紹介するつもりです(つもり、ね)。テンソル強度のちゃんとした定義はしません。実例が先にあったほうが定義を理解しやすいと思うからです。ただし、テンソル強度の意義とかココロは述べようと思います。
内容:
クライスリ圏にもモノイド積を
モナドがあんなに役に立つ理由/背景のひとつは、クライスリ圏が作れることでしょう。Cが圏で、(F, μ, η)がC上のモナドとします。μ、ηはそれぞれモナド乗法、モナド単位です。モナドFから作ったクライスリ圏を K = Kl(C, F) とします。Cを(クライスリ圏の)ベース圏と呼び、クライスリ圏Kの対象、射、結合、恒等射をそれぞれ(安直に)クライスリ対象、クライスリ射、クライスリ結合、クライスリ恒等射と呼ぶことにします。
圏の対象は a, b, c などの小文字で表します。(理由は、圏自身を表す記号とバッティングしないようにです。)ベース圏Cの上に、モナドFから作ったクライスリ圏Kを簡単に記述すると以下のとおり。
- Kの対象は、Cの対象と同じ。つまり、クライスリ対象は新しいものではありません*1。
- Kの射 f:a→b は、Cの射 f:a→F(b)。つまり、クライスリ射のCにおける余域はFで拡張されたbです。
- Kの結合はアレ。詳細は割愛しますが、モナド乗法(flatten)を使ってうまいことクライスリ結合を定義します。
- Kの恒等射 a→a は、Cの射 ηa:a→F(a)。モナド単位でクライスリ恒等射を定義します。
特筆すべきは、C→K という埋め込みがあることです。ベース圏Cは、クライスり圏Kの部分圏とみなせます。
さて、ベース圏Cがモノイド圏だとしましょう。以下では、モノイド圏を (C, +, 0) と書きます。「+」がモノイド積、「0」がモノイド単位です。記号は「+」を使いますが対称性は仮定しませんから注意してください。
Cがモノイド圏ならば、クライスリ圏Kl(C, F)もモノイド圏になるといいなー、と思うでしょう。C→K という埋め込みもモノイド構造を保つような埋め込みになって欲しいですよね。このような希望を実現するために、ベース圏のモノイド構造をうまいことクライスリ圏に持ち上げるメカニズムがテンソル強度です。
クライスリ圏Kが完全なモノイド圏になるためには、ベース圏C、モナドF、そしてテンソル強度にかなり条件を付けなくてはなりません。これらの条件がすべては満たされないとき、つまりクライスリ圏が完全なモノイド圏にならないときでも、それなりにテンソル強度は役に立ちます。
ここで老婆心で注意しておきますが、「テンソル強度」という言葉は物理や工学のテンソル計算を連想させますが、直接的な関係はありません。純粋に圏論的な概念だと理解して、語源を詮索しないほうがいいと思います。
ペアリングとテンソル強度
C = (C, +, 0)、F = (F, μ, η), K = Kl(C, F) として、クライスリ圏Kに具合のいいモノイド積があるとすれば、|K| = |C| なので、対象上ではCとKが同じモノイド構造を共有すべきです。a, b∈|K| に対して、Kにおける a+b は、Cにおける a+b と同じで、Kのモノイド単位はCのそれと同じとしましょう。こうすれば、Kの対象に関するモノイド構造は自明に定義できます。
問題は、射に関するモノイド構造、つまり、f, g∈K に対する f+g の定義できす。f:a→b, g:c→d in K とすると、これは f:a→F(b), f:c→F(d) in C を意味します。C内でfとgのモノイド積を作ると、f+g : a+b →F(c)+F(d) ですが、必要な射は、a+b → F(c+d) の形のものです。
K内でのfとgモノイド積があるとして、それをC内で見たものをf#gと表すことにします。今さっき言ったことから、f#g : a+b → F(c+d) in C です。f+g : a+b → F(c)+F(d) との差を埋めるためには、F(c)+F(d)→F(c+d) という射があって、しかるべき性質を持てばよさそうです。そういう好都合な射 F(c)+F(d)→F(c+d) をモナドFに伴なうペアリングと呼びます。
ペアリングは対象の対(c, d)ごとに決まるので、2つの対象で添字付けられた射の族(indexed family of morphisms)です。ペアリングを πc,d: F(c)+F(d)→F(c+d) と書くことにします。
ペアリングが、ベース圏のモノイド構造をクライスリ圏に持ち上げるメカニズムになりそうなことは分かりました。実は、ペアリングはもっと基本的な素材から組み立てられることが多いのです。それがテンソル強度です。テンソル強度も2つの対象で添字付けられた射の族で、次の形をしています。
- τa, b : F(a)+b →F(a+b)
左右が逆の形も必要です。
- τ'a, b : a+F(b) →F(a+b)
Cが対称モノイド圏のときは、τだけあればτ'を作り出せます。が、ここではτとτ'を組にして扱うことにします。実際のところ、(τ, τ') の形で扱うのが意味があるか? 非対称ケースでうまくいくのか? 僕はよく把握してませんが、(τ, τ') を使った記述のほうが分かりやすく感じます。
ペアリングとテンソル強度のこれ以上のことは実例とともに見ていくことにします。
Maybeモナドのテンソル強度
ここから先はベース圏を集合圏Setとします。もう混乱の心配がないので、Setの対象、つまり集合を英大文字とします。モナドはSet上で考えます。
Maybeモナドは、集合Aに新しい一点を加えて付点集合(pointed set)を作るだけのモナドです。なにもしない自明モナドに次いで簡単なモナドです。プログラミングとしての解釈は、未定義を含む関数(部分写像)を導入します。あるいは、最も簡単な形の例外の導入といっても同じです。集合Aに対して、Maybe(A) = A + {⊥} とします。⊥は未定義を表すシンボル、あるいは唯一の例外データです。
Maybeモナドのベース圏(集合圏Set)をモノイド圏と考えるのですが、直和をモノイド積(記号は「+」)、空集合(記号は0)をモノイド単位とします。つまり、(Set, +, 0)というモノイド圏を考えます。
まず、ペアリング πA,B: Maybe(A) + Maybe(B) → Maybe(A + B) は自然に定義できます。 Maybe(A) + Maybe(B) = (A + {⊥}) + (B + {⊥}) のなかで2回登場する⊥を1つに同一視する写像 (A + {⊥}) + (B + {⊥}) → (A + B) + {⊥} がペアリングです。
f:A→Maybe(B), g:C→Maybe(D) に対して、f # g = (f + g);πB,D と定義すると、演算# がMaybeモナドのクライスリ圏のなかでうまいことモノイド積になっていることが確認できます。
さて問題のテンソル強度ですが、次のような形です。
- τA,B : Maybe(A) + B → Maybe(A + B); (A + {⊥}) + B → (A + B) + {⊥}
- τ'A,B : A + Maybe(B) → Maybe(A + B); A + (B + {⊥}) → (A + B) + {⊥}
具体的な定義を書き下しませんが、要するに、直和の結合律と対称性を使って自然に対応付けるだけです。
左右のテンソル強度τ'(左), τ(右)があるとき、ペアリングπをどうやって作るかを証明図風の図で示してみます。
Maybe(A) + Maybe(B) -------------------------τA, Maybe(B) Maybe(A + Maybe(B)) -------------------------Maybe(τ'A, B) Maybe(Maybe(A + B)) -------------------------μA+B Maybe(A + B)
集合の要素のレベルで書き下してみると:
(a∈A または ⊥) または (b∈B または ⊥) : (A + {⊥}) + (B + {⊥})
--------------------------------------------------------------------
(a∈A または (b∈B または ⊥)) または ⊥ : (A + (B + {⊥})) + {⊥}
--------------------------------------------------------------------
((a∈A または b∈B ) または ⊥) または ⊥ : ((A + B) + {⊥}) + {⊥}
--------------------------------------------------------------------
(a∈A または b∈B ) または ⊥ : (A + B) + {⊥}
普段は意識しない当たり前のことをワザワザ書いているので、かえって分かりにくいかも知れません。絵を描くとか、プログラムで実装してみるとかして感じを掴んでくださいな。
ベキ集合モナドのテンソル強度
ベキ集合モナド(powerset monad)Powは、集合Aにそのベキ集合Pow(A)を対応させます。写像 f:A→B に対しては、Pow(f)(X) = {f(x)∈B | x∈X} と定義して共変関手とします。モナド乗法は、集合の集合の合併、モナド単位は単元集合で定義します。ベキ集合モナドのクライスリ圏の射は、非決定性の関数、多値関数、集合値関数などとしてプログラミング的に解釈されます。
ベキ集合モナドのときは、ベースとなるモノイド圏を (Set, ×, 1) とします。「×」は集合の直積、1は特定された単元集合です*2。
ベキ集合モナドに付随するペアリングは Pow(A)×Pow(B) → Pow(A×B) の形です、つまり部分集合のペア (X, Y)(X⊆A、Y⊆B)に対して、直積集合A×Bの部分集合を対応させます。その定義は単純で、(X, Y) |→ X×Y です。
Maybeモナドと同様に、πA,B : Pow(A)×Pow(B) → Pow(A×B); (X, Y) |→ X×Y とすると、f:A→Pow(B), g:C→Pow(D) に対して、f # g = (f×g);πB,D が、ベキ集合モナドのクライスリ圏のモノイド積を与えます。
テンソル強度は次のように与えられます。
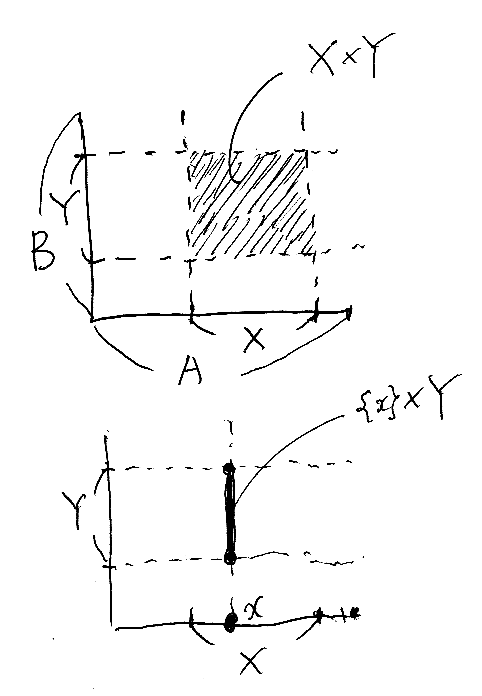
- τA,B : Pow(A)×B → Pow(A×B); (X, b) |→ X×{b}
- τ'A,B : A×Pow(B) → Pow(A×B); (a, Y) |→ {a}×Y
テンソル強度を組み合わせてペアリングを作る手順もMaybeモナドのときと同じです。
Pow(A)×Pow(B) -------------------τA, Pow(B) Pow(A×Pow(B)) --------------------Pow(τ'A, B) Pow(Pow(A×B)) -------------------μA×B Pow(A×B)
これを具体的に書き下すのはけっこうややこしいですがやってみます。
(X, Y) X⊆A, Y⊆B
--------------------------------------------------
X×{Y} = {(x, Y) | x∈X} ⊆ A×Pow(B)
--------------------------------------------------
{{x}×Y | x∈X} ⊆ Pow(A×B)
--------------------------------------------------
∪x∈X({x}×Y) = X×Y ⊆ A×B
A×Bを矩形として表現するなら、X×Yはその部分矩形ですが、{x}×Y という縦線の束として表現して、その縦線を集合X上で寄せ集めれば X×Y となる、ということです。これも図などを描きながら追いかければ分かるでしょう(そうしないと分からないかもしれません)。
テンソル強度は何が面白い
すべてのモナドにテンソル強度を付けられるわけではありませんが、既存のモナドでテンソル強度が定義できるものがあります。テンソル強度があれば、クライスリ圏がモノイド圏(そうでなくてもモノイド圏に近い)構造を持つのでずっと自由度が上がります。クライスリ圏上でもモノイド積を使ってリッチな構成が可能となります。モノイド積がないと出来ないことは多いので、これはありがたいです。
プログラムの例外処理と繰り返し処理は、分合律が成立する圏とトレース付きモノイド圏でモデル化できますが、分合律とトレースは、(部分的には)テンソル強度による解釈が可能です。ベックの分配法則とテンソル強度はよく似た概念です。物理に関連した線形代数(余代数のフォック空間)でもテンソル強度が使えそうです(これは僕の妄想段階ですけど)。