「絵算で見る「カザネスク/ステファネスク/ハイランド/長谷川の定理」」にて:
トレースについて今は説明しませんが、次のような公理で特徴付けられます。
- バニッシング(アクション性)
- タイトニング(自然性)
- スライディング
- スーパーポージング(強度性*1)
- ヤンキング
たまたま次の論文で、トレース付き対称モノイド圏の絵を見つけたので、少し説明します。
- Title: Diagrammatic Representations in Domain Specific Languages (2001)
- Author: Konstantinos Tourlas
- URL: http://www.lfcs.inf.ed.ac.uk/reports/02/ECS-LFCS-02-426/ECS-LFCS-02-426.ps
- pages: 158
僕が常々面白がっている話題の割には言及が少ないな>トレース付き圏。
内容
トレース付き対称モノイド圏の公理の絵
上記論文のP.103, P104にあった絵です。
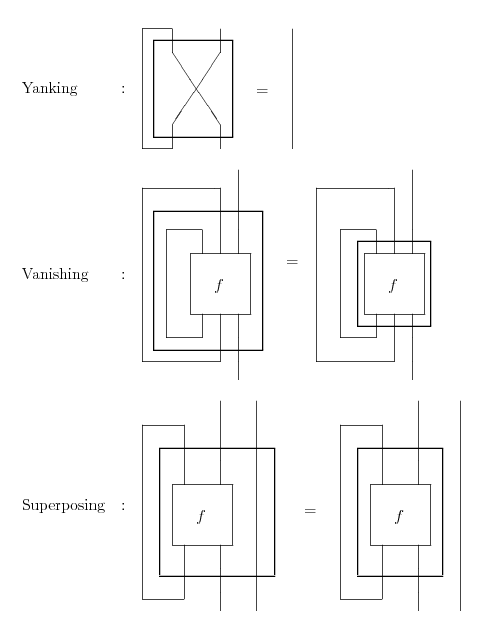
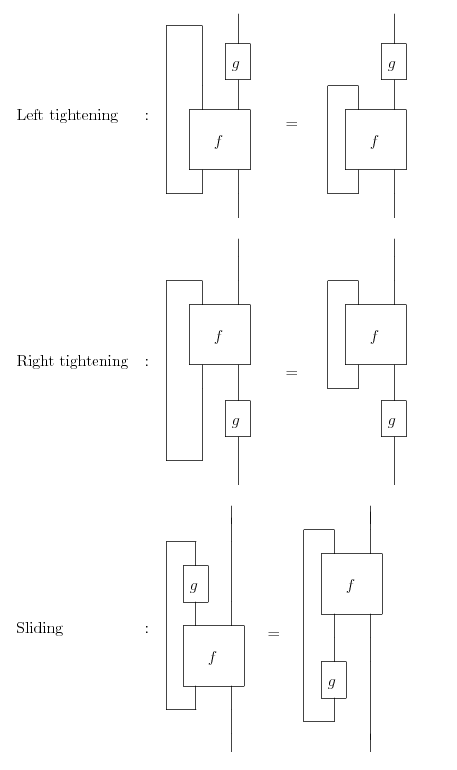
直線だけを使ったカクカクの絵ですね。方向は上から下です。ほとんどの絵が上下逆さまにしても同じですが、左タイトニングと右タイトニングの絵から「上から下」だと判断できます。反時計回りに90度回転すると、左から右の絵になります。
別な描き方の絵
内容的には同じことですが、長谷川真人さんの "Recursion from Cyclic Sharing: Traced Monoidal Categories and Models of Cyclic Lambda Calculi (1997)" http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.52.31 からコピーした絵も載せましょう。レイアウトの差から雰囲気が違います。
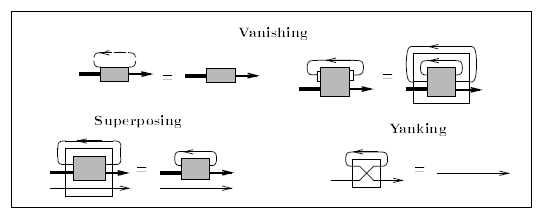
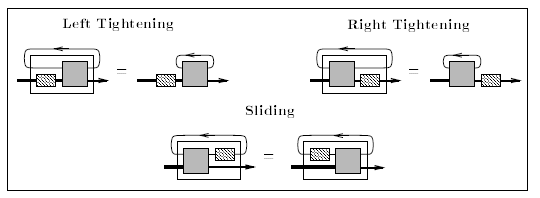
方向は左から右です。が、モノイド積の方向は下から上です。つまり、A+XのAが下でXが上に来ます。バニッシングの左側は TrA,B0(f) = f を表しています -- 先の図だとこの公理が欠けていましたが、気にするほどのことではありません。
テキスト数式による表現
いちおうテキスト数式でも書いておきます。モノイド積は足し算の形に書いて、σを対称(symmetry)だとします。f:X+A→X+B のとき、そのトレースは TrA,BX(f):A→B です。
ヤンキング
- TrX,XX(σX,X) = idX
バニッシング
f:A→B として:
- TrA,B0(f) = f
f:A+X+Y → B+X+Y として:
- TrA,BX(TrA+X,B+XY(f)) = TrA,BX+Y(f)
スーパーポージング
f:A+X→B+X として:
- TrA+Y,B+YX(idY + f) = idY + TrA,BX(f)
左タイトニング
f:A+X→B+X, g:Y→A として:
- TrY,BX( (g + idX);f ) = g;(TrA,BX(f))
右タイトニング
f:A+X→B+X, g:B→Y として:
- TrA,YX( f;(g + idX) ) = (TrA,BX(f));g
スライディング
f:A+X→B+Y, g:Y→X として:
- TrA,BY( (idA + g);f ) = TrA,BX( f;(idA + g) )
トレースって何なの?
f:A+X→B+X に対してそのトレース Tr(f) = TrA,BX(f) : A→B を作ることは、出力側(余域側)のXをループさせて入力のXに繋ぐことです。これは絵を見ればわかりますね。
上に挙げた絵を、説明の道具ではなくて、それ自身が対象や射だと思うと、トレースが結び目理論と直結するのは想像できるでしょう。実際、ブレイド図の圏にトレースを入れるともつれ(タングル)の圏が出来て、特殊なもつれとして結び目が得られます。ブレイドのマルコフ閉包はトレースの特殊な場合です。
上に挙げた絵は、ブレイドではなくてアミダ(対称群)なので、紐の交差に上下(手前と奥)の区別がありませんが、対称をブレイドに置き換えると、トレース付きブレイド付きモノイド圏(traced braided monoidal category)になります。いずれにしても、紐を伸ばしたり縮めたりズラしたり交差させたりする操作を公理化したのがトレース付き圏の公理で、トレースは紐をルーピングさせる操作になっています。
一方、トレース(trace)の語源は「行列のトレース」なんです。正方行列の対角成分の和ですね。行列の意味のトレースを特に対角和トレースと呼ぶことにします。テンソル計算では、対角和トレースを一般化した“トレース”を使います。一般化したトレースは縮約(contraction)と呼ばれることもあります。
有限次元ベクトル空間にテンソル積を考えた対称モノイド圏でトレース(縮約)を考えると、それは実際に圏論の意味のトレースになっています。後知恵で考えれば、テンソル計算はトレース付き圏よりコンパクト閉圏で定式化したほうがいいと思いますが、ともかく、トレース付き圏の起源のひとつは線形代数です。
紐の操作とテンソル計算の類似性に気づいて、それを利用した計算法(つまり絵算)を編み出した人(のひとり)がペンローズですね。
紐がからんだり結んだりと、線形代数(テンソル代数)がなんで同じ公理で記述できるんだ? と、それが不思議ですが、位相的場の理論(TQFT)の枠組みを使うと、図形にベクトル空間を対応付けることができて、図形の圏とベクトル空間の圏を行ったり来たりできるようになります。トレース付き圏やコンパクト閉圏は、公理的TQFTの文脈で理解するのが一番良いんじゃないだろうか、と思います。よく分かってないくせにエラソーに言ってます>自分。
僕にはサッパリわからない事ですが、トレースには強い物理的な背景があるそうです。当然ながら、TQFTも物理が起源ですし。ブレイドと線形代数を結びつけるヤン/バクスター方程式も元々物理だし、テンパリー/リーブ代数も統計物理から出てきたとか。
さて、計算(computation)との関係ですが、、、それは節を改めて。
論理と計算とトレース
コンパクト論理で考えると、トレースを取ることは、次のようなシーケント推論図になります。
A, X → B, X
----------------
A → B
ただし、前提と結論で共通の命題Xが消えてしまうのではなくて、Xを消した痕跡が残り続けるような推論です。ここでもカリー/ハワード対応が成立しています -- ある種のコンパクト論理と平面ラムダ計算とテンパリー/リーブ圏の関係は、アブラムスキーの次の論説(以前の圏論勉強会テキスト)で解説されています。
- "Temperley-Lieb Algebra: From Knot Theory to Logic and Computation via Quantum Mechanics"(http://web.comlab.ox.ac.uk/oucl/work/samson.abramsky/tambook.pdf)
一方でピーター・セリンガーは、トレースは論理の存在記号(∃)と似てるとか言っています。これは、ベクトル空間とテンソル積の圏が、関係と直積の圏と似てることが背景です。ボブ・クックも、ヒルベルト空間の圏と関係の圏が似てるとほのめかしていました。論理的な存在の確認(∃)と、テンソル計算の縮約と、総和(Σ)や積分(∫)が似ていて、それらはトレースの形をしています。存在と積分の類似性は、マスロフ流のベキ等解析(idempotent analysis)でかなり明らかになります。
セリンガーは、論理の存在記号や縮約が起源となるトレース(乗法的トレース)と、それとは毛色が違うトレース(加法的トレース)があるんだ、とも言っています。加法的なトレースの例はクリーネスターです。クリーネスターは、形式言語理論やオートマトン理論の主役です。また、繰り返し制御や不動点とも密接に関係します(というか、事実上同じモノ、「絵算で見る「カザネスク/ステファネスク/ハイランド/長谷川の定理」」参照)。
先ほど、トレースは物理と関係が深いと言いましたが、それだけでなく論理や形式言語理論や計算とも関係する、ということは、これらの分野を横断する何らかの原理があるのかもしれません。… てなことは、バエズ、アブラムスキー、ジラールなんかが言ってます。
物理(場の量子論)と形式言語理論(オートマトン理論)が似てるって話は、マーク・ホプキンス(Mark W. Hopkins)がかつてWebページで指摘していました。そのWebページはなくなってしまったのですが、僕の印象には強く残っています。
もっと直接的かつ露骨にトレース付き圏(やコンパクト閉圏)が計算(computation)に使える例といえば、フローチャートとgoto文によるオシャレなプログラミングでしょう。ステファネスク師匠の路線ですね。これを話しだすとキリがないので、関連記事だけ:
それともうひとつ実務に直結する話は、COMET(逆HTTP)を含めたHTTP通信のフローがコンパクト閉圏になること。
コンポネントアーキテクチャの多くは、潜在的にトレース付き圏やコンパクト閉圏使ってますしね。
- 「DI(依存性注入)からどこへ行こうか その1」とそこからのリンク
- 「「物理系実務者のための圏論入門」への補遺+檜山の戯言」の最後のほう
というわけで、トレース付き圏もそこいらじゅうにワサワサいるのです。