「サブオブジェクト・クラシファイアーの素朴な説明」とかで、「モノ射の引き戻しはモノ射である」ことを使ってるんですが、念のため確認しようとしたら手間取った。で、その経過を貼っておきます。
とりあえず絵だけ。後で説明を足します、たぶん。([追記 date="2011-01-14"]説明を追加。[/追記])
絵でモノ矢印(>-->)を間違ってエピ矢印(-->>)で描いていますが、修正する気ありません。あしからず。
当該の四角形
引き戻し(pulback)の四角形が以下に何度も出てくるのですが、「The=今話題にしているその…」という意味で「当該」という言葉を使うことにします。んで、これから扱う当該四角形は次のようなもの。
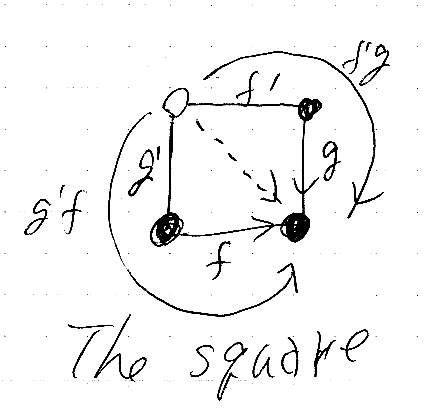
射f, gと黒丸の対象は与えられていて、白丸の対象(ファイバー積とも言います)とf', g'が見つかります/作れます、という状況ですね。射の結合は図式順で f';g のように書きますが、結合(composition)の演算記号であるコロンも省略して f'g とも書きます。
引き戻し四角形の定義
p.b.(pull back の略)と書かれている四角形(当該四角形)が引き戻しであるとは、次のことです。
- まず、当該四角形は可換です。可換な四角形は内部を斜線で塗って表します。
- 当該四角形とは別にバッテンの対象と、バッテンから図のような射が与えられて可換な四角形(塗ったヤツ)が出来るとき、斜線で塗った領域を可換にする射sが一意的に存在する。
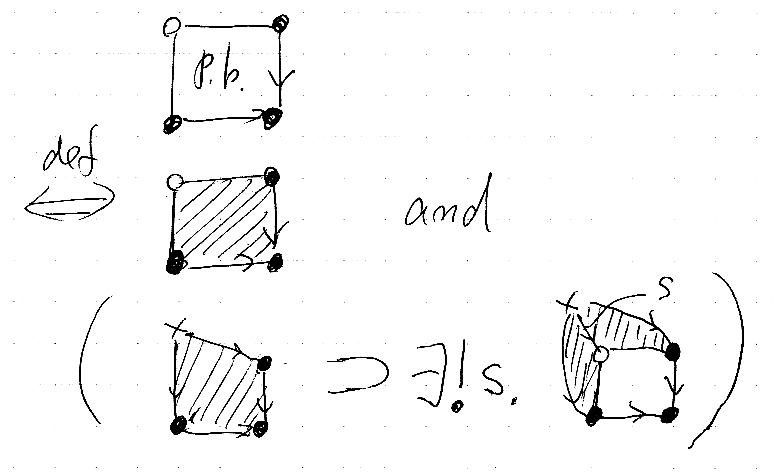
「⊃」は論理の含意記号です。「∃!」は一意的存在を表す記号。絵と論理式を混ぜた表現ですね。
結論の記述と証明の前半
次の図の一番上段(0)は示すべき命題の記述で、「mがモノ射で、当該四角形が引戻しなら、m'もモノ射」ということです。矢印「->>」はエピ射の記号なんですが、こりゃ僕の間違いです。ここだけ、「->>」をモノ射と思ってください。
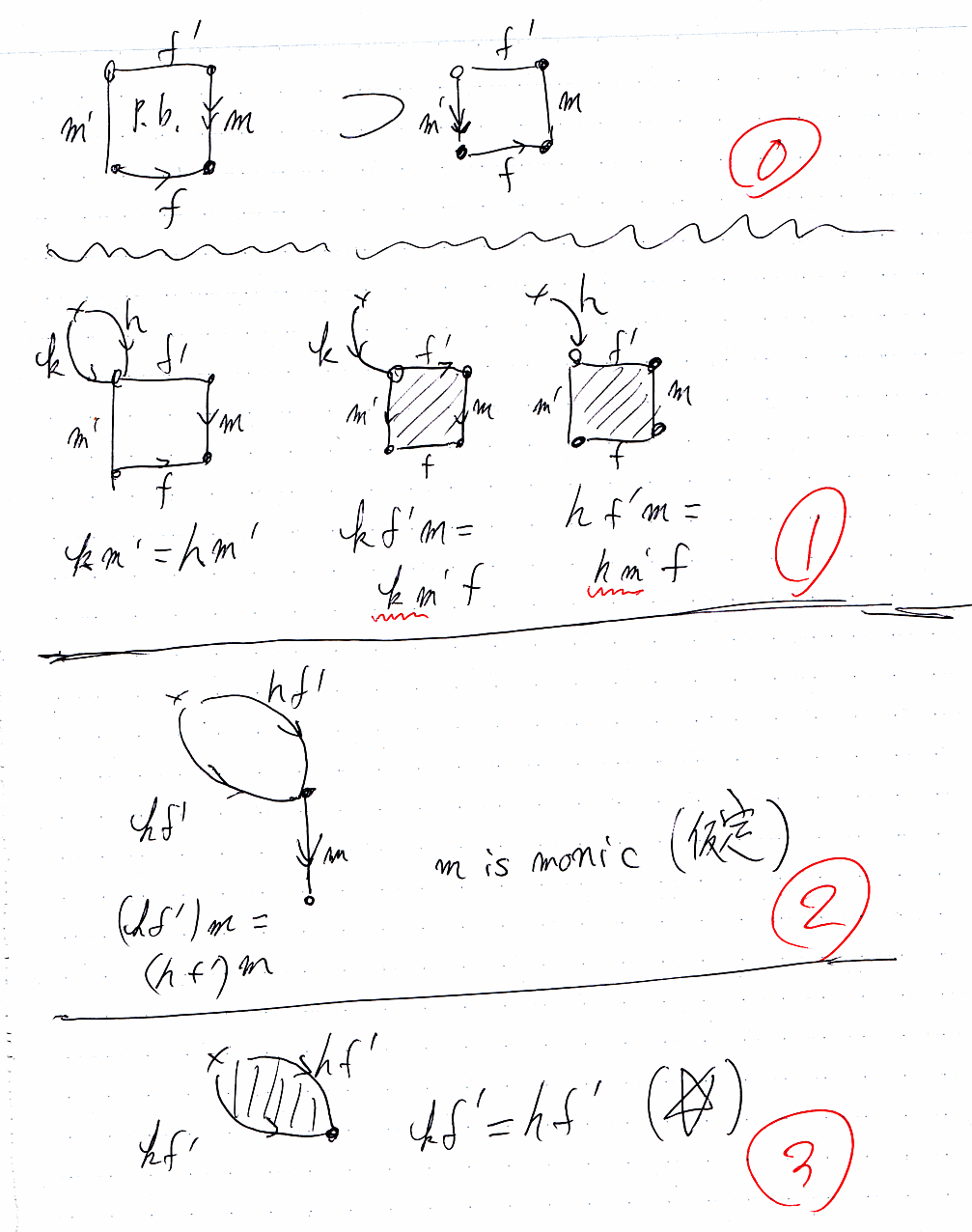
(1)の段、図の左端のような k, h が与えられたとします。km' = hm' という等式条件が付きます。この仮定から、k = h が導ければm'がモノだと言えます。
当該四角形は引き戻し、したがって可換四角形なので、kf'm = km'f と hf'm = hm'f は言えます。km' = hm' は、(1)の冒頭で仮定しておいた事なので、kf'm = hf'm が言えます。
kf'm = hf'm は、(kf')m = (hf')m と書けます。mがモノなことは最初の仮定ですから、kf' = hf' が言えます。これが、(2) と (3) の内容。kf' = hf' という等式には星印(☆)を付けておきます。
証明の後半
(1)で導入したhに注目します。バッテンから右下の対象まで至る道は、hf'm と hm'f です。当該四角形は可換だったので、f'm = m'f 、したがって、hf'm = hm'f となり、バッテンを含む外側の四角形が可換となります。ところで、もとの当該四角形は引き戻しだったよねー、と。そこまでが(4)。
当該四角形は引き戻し四角形だったので、(5)のsのような射が一意的に存在するのでした。このsが実はkに他ならないことを示しましょう。(1)の最初で導入した仮定から km' = hm'、それと(☆)から kf' = hf'。よって、(6)の斜線で塗った部分は可換となります。当該四角形も可換なので、外側の四角形も可換です。ということは、外側の四角形とkはプルバックの条件に出てくるsじゃないですか。そんなsは、存在すれば1つしかないので、k = s と言えます。まったく同じ論法で h = s も言えます。
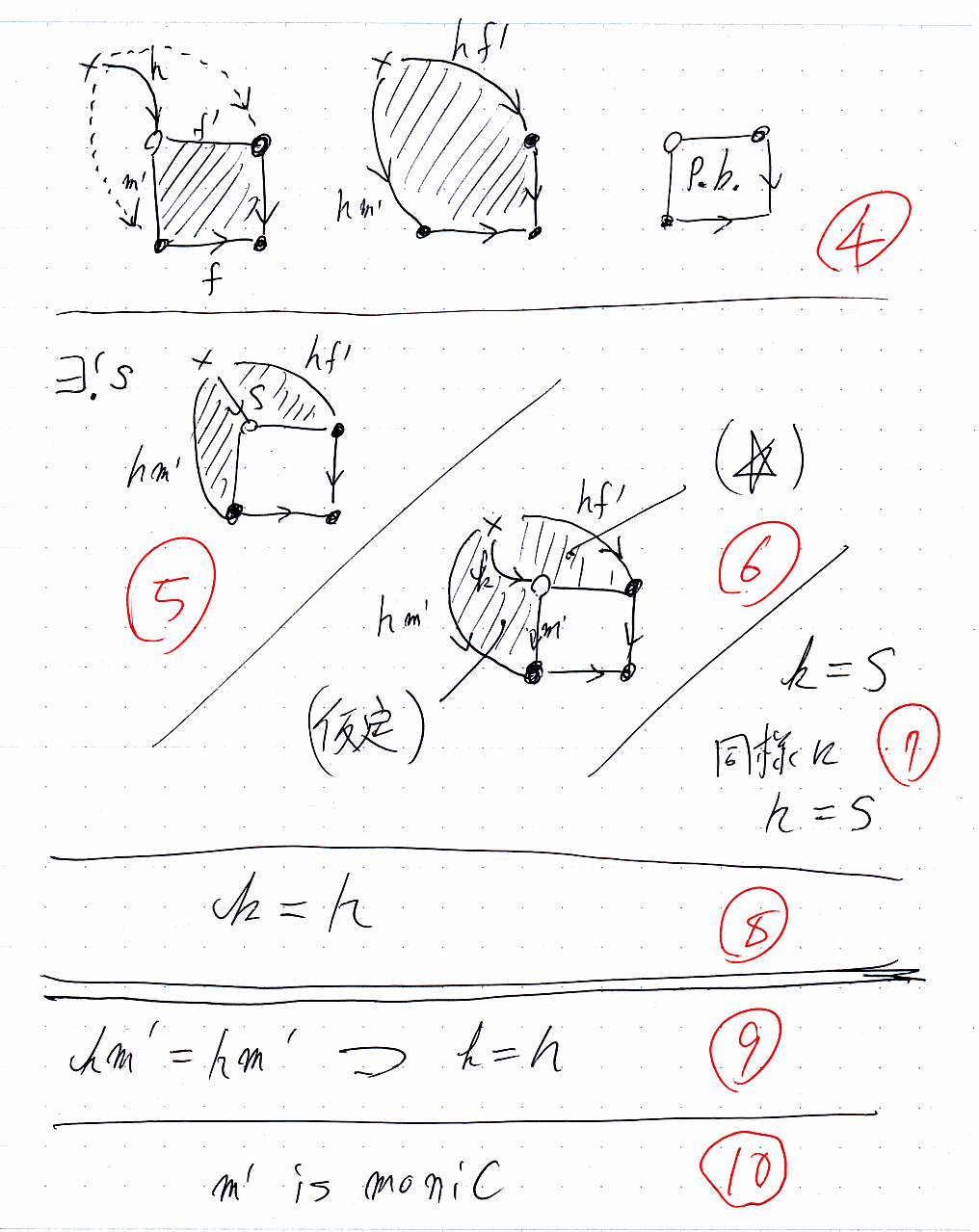
k = s、h = s ですから、k = h 。ここで、(1)の最初のほうの仮定を振り返れば、「km' = hm' ならば k = h」が演繹できたことになります。これはつまり、m' がモノだということです。
当該四角形が引戻しで、m がモノであるなら、m' もモノなのです。これが主張したかったことです。