樹形タプルの世界 - 檜山正幸のキマイラ飼育記 (はてなBlog)

高階関数は扱わないけど、タプルは扱うようなラムダ計算のモデルを作ろうと思いました。まず、基礎データの集合Dを固定します。Dからタプルを作るので、Dⁿ とかは扱います。関数型はないので、ベキ（例えば、D^D）は必要ありません。そうであるなら、意味論のユニバースとなる圏U_Dは比較的簡単に構成できそうです。

Partialを、集合と部分写像の圏として、n, mを自然数（非負整数）として U_D(n, m) = Partial(Dⁿ, D^m) として定義される圏U_Dで十分だろう、と思ったのですが、どうもうまくありません。自然数よりもう少し一般的な“図形”s, tを使って、U_D(s, t) = Partial(D^s, D^t) とする必要がありました。ここで、s, tはある種のツリーです。D^t などの意味も新たに定義する必要があります。

そんな事情で樹形タプルという概念を考えました。

内容：

マルバツツリー
樹形タプル
マルバツツリーの表現と特徴的な量
マルバツツリーの演算
樹形タプルの圏

マルバツツリー

ノードがマル（●）またはバツ（×）であるようなツリーを考えます。ただし、次の制限があります。

末端ノード（リーフ）にしかバツは許されない

このようなツリーをマルバツツリーと呼ぶことにします。このネーミングはもちろんイイカゲンなものです。真面目に名前を付けるほどの概念じゃありません。

いくつかのマルバツツリーの例を挙げます。図で、（一番左を除いて）ルートは白丸になっていますが、これはルートであることを明示するために白抜きにしてあるだけで、ルートもマルノードです（気になるなら、ルートも黒塗りにしてください。）。

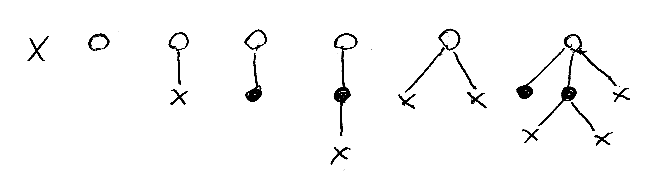
マルバツツリーのバツノードには、なにか値を割り当てることができるとします。マルノードには値を付けられませんが、子ノードをグルーピングするので、マルノードは丸括弧で表現することにします。バツノードすべてに整数値 1 を割り当てた場合、上図のツリーは次のように表現できます。

1
()
(1)
(())
((1))
(1, 1)
((), (1, 1), 1)

もちろん、バツノードには1以外の値を自由に割り当てることができます。例えば、右端のツリーの×の出現に、3, 0, 1 と値割り当てをして ((), (3, 0), 1) とすることもできます。

樹形タプル

Dが集合、tがマルバツツリーであるとき、tのバツノードにDの値を割り当てて作れる値付きツリーを、形状（shape）がtのD値樹形タプル（tree-shaped tuple）と呼ぶことにします。形状がtのD値樹形タプルの全体を TT(t, D) と書きましょう。

TT(t, D) を D^t と書きたいのですが、通常の直積ベキ Dⁿ との混乱を防ぐため D^←t と書くことにします。通常の Dⁿ の要素に対応する樹形タプルを定義するため、非負整数nに対する [n] というマルバツツリーを定義します。その定義は次のようになります。

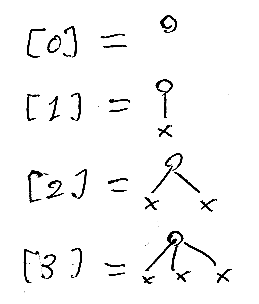
ルートのマルノードが1つあって、n個のバツノードが子ノードとしてぶら下がっています。このようなマルバツツリー [n] を使えば、次の同型が言えます。

Dⁿ ≒ D^←[n] = TT([n], D)

n個の子ノードに、左から右に番号 1, 2, ... を付けると約束すれば、Dⁿ と TT([n], D) の同型は規範的（canonical）だと言えます。ただし、D⁰ と D¹ に関しては、別な同型を選ぶこともできます。<0>, <1> を次のように定義します。

<0> = 空集合 = ノードが1つもないマルバツツリー
<1> = ただ1つのバツノードからなるマルバツツリー

明らかに：

D⁰ = 単元集合 ≒ TT(<0>, D)
D¹ = D ≒ TT(<1>, D)

DをTT([1], D)と考えるか、TT(<1>, D)と考えるかは、どうでもいい恣意的な話です。いずれにしても、Dⁿ（n = 0, 1, 2, ...）は樹形タプルの世界に埋め込めるということです。

マルバツツリーの表現と特徴的な量

マルバツツリーのテキスト表現としては、先週の記事で示した方法を使ってもいいですし、丸括弧を使う記法でもいいでしょう。また [n], <0>, <1> のような記法も使えます。最初の図に挙げたマルバツツリーをそれらの記法で書いてみましょう。（○と●は、どちらもマルノードです。）

× = <1>
○ = () = [0]
○{×} = (×) = [1]
○{●} = (())
○{●{×}} = ((×))
○{×, ×} = (×, ×) = [2]
○{●, ●{×, ×}, ×} = ○{●, [2], <1>} = ((), (×, ×), ×)

tがマルバツツリーのとき、length(t) を次のように定義します。

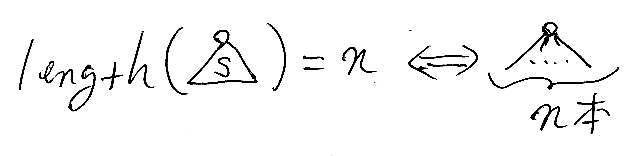
便宜上 length(<0>) = 0 としておきます。lengthの具体例は：

length(×) = 0
length(○) = 0
length(○{×}) = 1
length(○{●}) = 1
length(○{●{×}}) = 2
length(○{×, ×}) = 2
length(○{●, ●{×, ×}, ×}) = 3

マルバツツリーtのなかに含まれるバツノードの個数を dim(t) とします。dimの具体例は：

dim(×) = 1
dim(○) = 0
dim(○{×}) = 1
dim(○{●}) = 0
dim(○{●{×}}) = 1
dim(○{×, ×}) = 2
dim(○{●, ●{×, ×}, ×}) = 3

[n] に関しては次の等式が成立します。

length([n]) = n
dim([n]) = n

次の同型は容易に構成できます。

D^←t ≒ D^←[dim(t)]

マルバツツリーの演算

Dⁿ×D^m ≒ D^n+m のような同型が成立しますが、樹形タプルに関しても同じような公式を示すために、マルバツツリーの演算を定義しておきます。

□と△という2つの演算を次のように定義します。

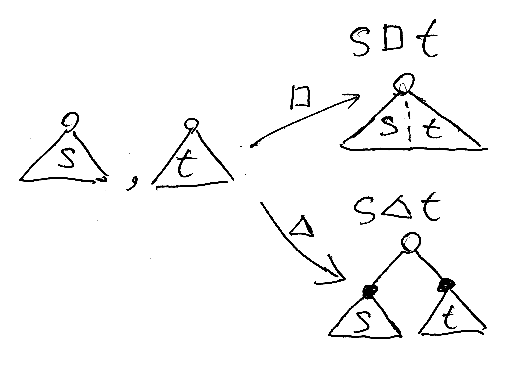
この図は、sもtもマルのルートノードを持つ場合ですが、s, tのどちらかまたは両方が空ツリー<0>のときも s□t, s△t を定義できます。バツノードだけのツリー×が入るとs□tはうまく定義できませんが、s△t は大丈夫です。

ツリーがまったく同じ形状でピッタリ重なるときに「等しい」とみなすことにします。演算□は結合律が成立し、[0]（または<0>）が単位になります。

(s□t)□u = s□(t□u)
[0]□t = t□[0] = t

しかし、△は結合律が成立しません。t△s を作るとき新しいノードが増えるので単位もありません。なお、(s△t△u) は、(s△t)△u でも s△(t△u) でもなくて、新しいルートノードの下に s, t, u を兄弟としてぶら下げたツリーを意味するとします。

次の等式が成立します。

length(s□t) = length(s) + length(t)
dim(s□t) = dim(s) + dim(t)
length(s△t) = 2
dim(s△t) = dim(s) + dim(t)

D^←[n]×D^←[m] ≒ D^{←([n]□[m])} も D^←[n]×D^←[m] ≒ D^{←([n]△[m])} も成立しますが、その根拠は D^←t ≒ D^←[dim(t)] という同型と、dim(s□t) = dim(s) + dim(t)、dim(s△t) = dim(s) + dim(t) です。

[n]□[m] = [n+m] ですが、[n]△[m] = [n+m] ではない点に注意してください。

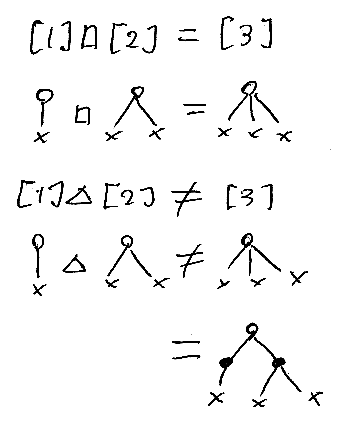
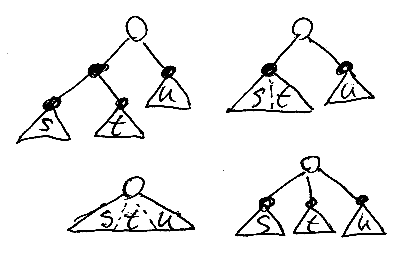
下の図は、演算□と△により作られたツリーの例で、(s△t)△u, (s□t)△u, (s□t□u), (s△t△u) です。

樹形タプルの圏

マルバツツリーの全体をMBTreeとします。MBTreeには、空なツリー<0>や×だけのツリー<1>も含まれます。

Dを空でない集合として、圏U_Dを、MBTreeを対象集合として、ホムセットが次のように定義された圏だとします。

U_D(s, t) = Partial(D^←s, D^←t)

混乱の心配がなければ、D^←t を D^t と書くことにして、次のようにも書きます。

U_D(s, t) = Partial(D^s, D^t)

射 f:s→t （f∈U_D(s, t)）は部分関数ですが、fの関数としての始域がsということではありません。dom(f) = s ということと、関数fの始域が何であるかは別な話です。（部分）関数fの始域を Dom(f) と書くことにすると、f:s→t in U_D のとき Dom(f) = D^←s です。あるいは、次の2つの主張が（定義より）同値だとも言えます。

f:s→t in U_D
f:D^←s→D^←t in Partial

圏U_Dはデカルト圏にすることができます。MBTreeで定義された演算に△と□がありました。□のほうが扱いやすいですが、直積としては△を使うことにします。<0>も[0]も、その他 dim(t) = 0 であるマルバツツリーはなんでも直積単位に選べますが、ここでは [0] を識別された単位（distinguished unit）として 1 と書きます。

直積を定義する構造同型 α_s,t,u:(s△t)△u→s△(t△u)、λ_t:1△t→t、ρ_t:t△1→t、射影 π¹_s,t : s△t→s, π²_s,t : s△t→t が定義できて、デカルト圏の公理を満たすことを示せます。<0>と<1>を取り除いてしまい、演算□と単位[0]によりデカルト構造を定義することもできます -- このほうが簡明です。微妙に違うデカルト構造を複数持てることは注意しておいたほうがいいでしょう。

(U_D, △, 1) はデカルト圏ですが（このままでは）デカルト閉圏ではありませんから、高階関数は扱えません。しかし、関数計算のモデルとしては U_D でも十分な場合もけっこうあります。