「アイレンベルグ/ムーア圏 その1」において、アイレンベルグ/ムーア圏の定義を述べ、「アイレンベルグ/ムーア圏 その2:リストモナドのとき」で典型的な事例を紹介しました。さらに別な例を挙げます。今日は、Maybeモナドのアイレンベルグ/ムーア圏がどんな圏になるかを調べてみます。
内容:
Maybeモナド(付点モナド)
圏C上のモナドを (M, η, μ) として、「アイレンベルグ/ムーア圏 その2:リストモナドのとき」と同じような書き方でMaybeモナドを定義しておきます。
- C := Set
- M0(A) := Maybe<A> := A + 1
- M1(f:A→B) :=Maybe.lift<A, B>(f):(A + 1)→(B + 1)
- ηA := Maybe.embed<A>:A→(A + 1)
- μA := Maybe.join<A>:((A + 1) + 1)→(A + 1)
1は特定された単元集合(singleton set)です。1の唯一の要素は何でもいいのですが、⊥(ボトム)記号にしておきます。Maybe<A> := A + 1 なので、Maybe<A> := A + {⊥} です。注意すべきは、+ が直和(排他的な合併)を表すので、⊥!∈A (!∈ は「∈の否定」)を前提としていることです。Aには属さないナニカを取ってきて、それをAに追加するわけです*1。(A + 1) + 1 は、(A + {⊥}) + {⊥} ですが、これは A + {⊥} ではなくて、A + {⊥1, ⊥2} のように考えます。
lift, embed, joinは、なんか無理矢理に名前を付けた感じですが、次のような定義になります。
- for-all x in A { Maybe.lift<A, B>(f)(x) = f(x) }, Maybe.lift<A, B>(⊥) = ⊥
- for-all x in A { Maybe.embed<A>(x) = x }
- for-all x in A { Maybe.join<A>(x) = x }, Maybe.join<A>(⊥1) = ⊥, Maybe.join<A>(⊥2) = ⊥
最後のMaybe.joinは、2つのボトムを1つのボトムにまとめるものです。次の図のような雰囲気です。
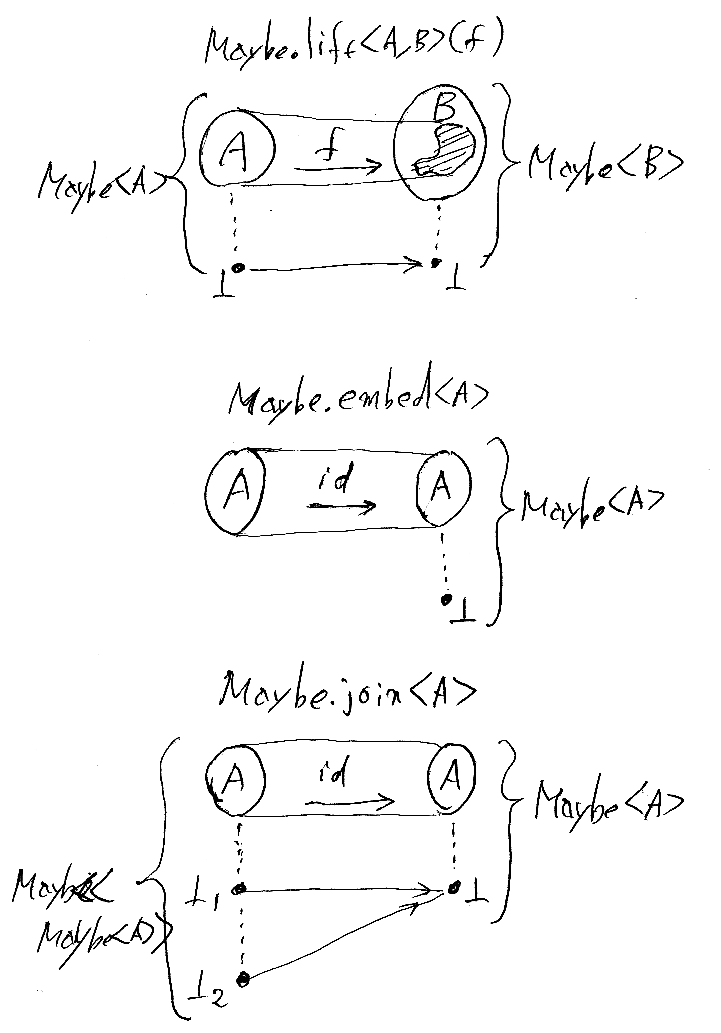
こうして定義されたMaybeモナドは、与えられた集合Aに1点を追加する操作なので、付点モナドと呼んでもいいでしょう。
Maybeモナドの代数
C上のモナド (M, η, μ) の代数とは、とりあえずは a:M(A)→A in C という射でした。Maybeモナドの場合は、a:(A + {⊥})→A となります。代数が満たすべき条件は次の図が可換になることでした。
A - η_A --> M(A) | | | a | | v v A ---------> A M(M(A)) - M(a) --> M(A) | | μ_A a | | v v M(A) ----- a -----> A
MがMaybeモナドのときに等式で書き下せば:
- for-all x in A { a(Maybe.embed<A>(x)) = x }
- for-all z in (A + {⊥1, ⊥2}) { a(Maybe.lift<Maybe<A>, A>(a)(z)) = a(Maybe.join<A>(z)) }
以下で、これらの等式を噛み砕いて分析してみましょう。
Maybeモナドの代数の単位律
Maybe代数の重要な性質は一番目の等式から出てきます。
- for-all x in A { a(Maybe.embed<A>(x)) = x }
Maybe.embedの定義 Maybe.embed<A>(x) = x を使うと:
- for-all x in A { a(x) = x }
となります。代数の演算aは、A + {⊥} 上で定義されていたので、a(⊥) = e (e∈A) と置きましょう。すると、aは次のように記述できます。
- a(x) = x if x in A
- a(⊥) = e (e∈A)
結局、Maybeモナドの代数 (A, a) は、Aの一点であるeを指定すれば決まることになります。そこで、Maybe代数を、「集合Aと演算aの組」ではなくて、「集合AとAの一点eの組」で表すこともできます。(A, e) ですね。(A, e) から (A, a) を再現するには、すぐ上のようにaを定義すればいいのです。
Maybeモナドの代数の結合律
次に二番目の等式です。
- for-all z in (A + {⊥1, ⊥2}) { a(Maybe.lift<Maybe<A>, A>(a)(z)) = a(Maybe.join<A>(z)) }
二番目の等式は面倒そうですが、A + {⊥1, ⊥2} = (A + {⊥1}) + {⊥2} として、A + {⊥1} の部分と {⊥2} に分けてみると次のようです。
- for-all y in (A + {⊥1}) { a(Maybe.lift<Maybe<A>, A>(a)(y)) = a(Maybe.join<A>(y)) }
- a(Maybe.lift<Maybe<A>, A>(a)(⊥2)) = a(Maybe.join<A>(⊥2))
一番目をさらに分解すると:
- for-all x in A { a(Maybe.lift<Maybe<A>, A>(a)(x)) = a(Maybe.join<A>(x)) }
- a(Maybe.lift<Maybe<A>, A>(a)(⊥1)) = a(Maybe.join<A>(⊥1))
- a(Maybe.lift<Maybe<A>, A>(a)(⊥2)) = a(Maybe.join<A>(⊥2))
どうにもクソ鬱陶しい等式群ですが、Maybe.による修飾や型パラメータを省略すると多少はスッキリします*2。
- for-all x in A { a(lift(a)(x)) = a(join(x)) }
- a(lift(a)(⊥1)) = a(join(⊥1))
- a(lift(a)(⊥2)) = a(join(⊥2))
絵を描けば、これらの等式がたいした内容を持たないないことが分かるでしょう。
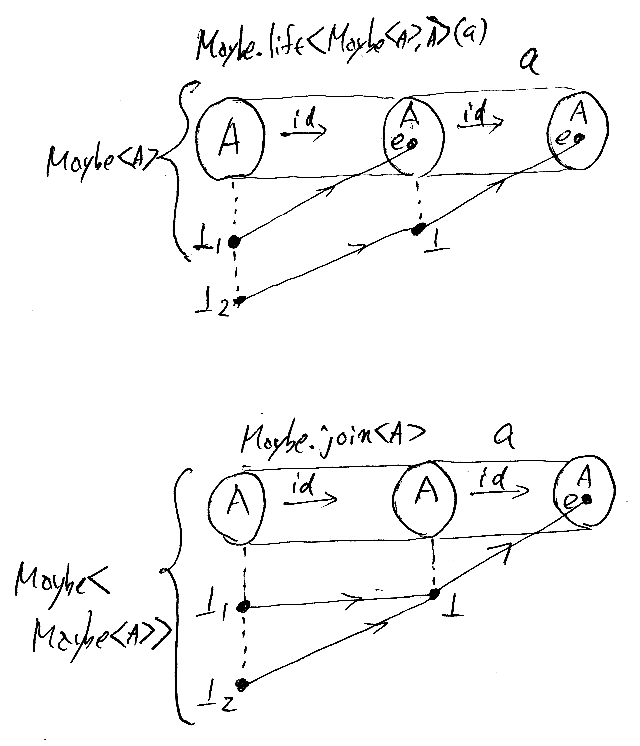
実際、定義に従って計算すると、等式は次のように簡略化されます。
- for-all x in X { a(x) = a(x) }
- a(a(⊥1) = a(⊥)
- a(⊥) = a(⊥)
一番目と三番目はまったくのトートロジー、二番目は a(e) = e ですが、これも新しい事実ではありません。つまり、Maybeモナドに関して言えば、結合律から新しい情報は何も出てきません。別な言い方をすると、Maybe代数は単位律だけの制約を受けるということです。
付点集合の圏
付点集合(pointed set; 基点付き集合)とは、集合Aにその一点eが指定されたものです。付点集合を (A, e) で表しますが、e∈A であることを強調して、(A, eA) とも書きます。さらには、記号の乱用で A = (A, eA) のようにも書きます。
(A, eA), (B, eB) が2つの付点集合のとき、写像 f:A→B が、f(eA) = eB であるとき、付点集合のあいだの射だとします。付点集合とその射の全体は圏をなします。その圏をPtSetとしましょう。空集合は基点を持てないので付点集合とはならないことに注意してください。
Mabyモナド(付点モナド)の代数 (A, a) があると、(A, a(⊥)) という付点集合を定義できます。逆に、付点集合 (A, eA) があれば、a(⊥) = eA (その他部分は恒等)としてMaybe代数が定義できます。
f:A→B がMayb代数の射 (A, a)→(B, b) であるとは次の図式が可換になることです。
Maybe<A> - a --> A | | lift(f) f | | v v Maybe<b> - b --> B
a(⊥A) = eA ∈A, b(⊥B) = eB ∈B とすると、この可換図式から f(eA) = eB が従います。つまり、fは付点集合の射 (A, eA)→(B, eB) を定義します。逆向きの対応も作れることから、Maybeモナドのアイレンベルグ/ムーア圏 EM(Set, Maybe) は、付点集合の圏PtSetと圏同値になります。
不思議なことに、有名なモナドのアイレンベルグ/ムーア圏を作ると、よく知られた圏が現れます。EM(Set, List) = Mon(Set) と EM(Set, Maybe) = PtSet という圏同値が登場しましたが、他の例でもお馴染みの圏が再現されることが多いようです。実際には、この現象は不思議でもなんでもなく、同じ実体を別な側面から見ているだけのことかも知れませんけどね。