二重圏の具体的な定義

昨日の記事で二重圏（double category）について触れました。二重圏は2次元の圏の一種です。2次元の圏は、n=2 の場合のn-圏（高次圏）です。

高次圏（higher category）の定義は一般に面倒です。DblCat := Cat(Cat) のように、圏論特有の機械仕掛け（machinery）を使えばコンパクトな記述で済むこともありますが、これだと具体性がなく実感が湧きません。具体的に書こうとすると、演算も法則も多くてとても煩雑です。

中庸（＝妥協案）を取ると、具体的な定義をだいたいは書いて、あとは端折る方法です。「以下同様、あとは分かるよね」とか「詳細は宿題」ってやり方。この記事でも、慣例に従い(？)細部は省略した具体的な定義を述べてみます。記法を工夫して出来るだけ分かりやすくするようには試みます。

Dが二重圏だとすると、この二重圏から4つの普通の圏（ordinary category、1次元の圏）が得られます。それらの圏を D_h1、D_v1、D_2h、D_2v とします。それぞれの圏と、4つの圏の相互関係がキチンと記述できれば、それで二重圏Dを定義できることになります。

二重圏を構成する素材が4種類あるので、まず素材の集合（小さいとは限りません）を列挙しておきます。素材の集合はイタリックではなくて通常の書体を使うことにします。

1. D₀ ： 0-セルの集合
2. D_h1 ： 水平1-セル（horizontal 1-cell）の集合
3. D_v1 ： 垂直1-セル（vertical 1-cell）の集合
4. D₂ ： 2-セルの集合

0-セルを対象、水平1-セルを水平射、垂直1-セルを垂直射と呼ぶこともあります。これら4種の素材は、次の図のような四角形を構成します。

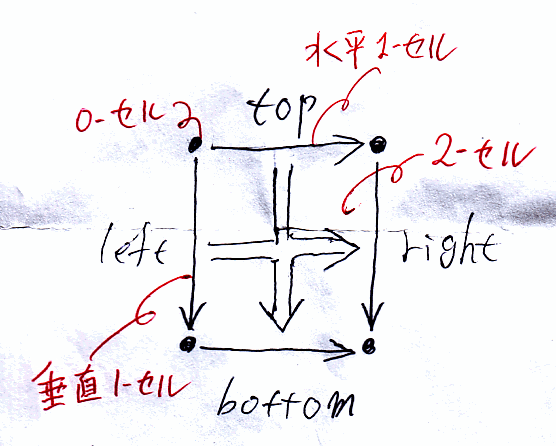
0-セルは点、1-セルは方向を持った矢印、2-セルは2次元の面です。2-セルも方向を持つのですが、この図における left⇒right の方向と top⇒bottom の2つの方向を持つと考えます。

既に添字として出てきている略記（符丁）の意味は次のとおりです。

1. 0 ： 0-セル
2. h1 ： 水平1-セル
3. v1 ： 垂直1-セル
4. 2 ： 2-セル
5. 2h ： 水平方向に見た2-セル（2-cell as a horozontal arrow）
6. 2v ： 垂直方向に見た2-セル（2-cell as a vertical arrow）

1つの二重圏Dから得られる4つの圏の概要を書いておくと：

1. D_h1 = (D₀, D_h1, dom_h1, cod_h1, id_h1, comp_h1)
2. D_v1 = (D₀, D_v1, dom_v1, cod_v1, id_v1, comp_v1)
3. D_2h = (D_v1, D₂, dom_2h, cod_2h, id_2h, comp_2h)
4. D_2v = (D_h1, D₂, dom_2v, cod_2v, id_2v, comp_2v)

これって添字を変えてコピーしてるだけじゃないか？ はい、そうなんです。大雑把に言えば、D_h1は、点と横の矢印で作られる圏、D_v1は、点と縦の矢印で作られる圏、D_2hは、縦の矢印（横じゃない！）と横方向で考えた四角面で作られる圏、D_2vは、横の矢印（縦じゃない！）と縦方向で考えた四角面で作られる圏です。

comp_h1とcomp_2hは、水平結合または横結合と呼ばれます。comp_v1とcomp_2vは、垂直結合または縦結合と呼ばれます。横結合の記号にアスタリクス（'*'）がよく使われることから、横結合をスター結合とかスター積と呼ぶこともあります。

D_h1、D_v1、D_2h、D_2vが圏の構造を持つだけでなく、二重圏D全体として、四角のタイルを貼りあわせてうまく計算ができるような法則性を持ちます。

二重圏でもそれなりに複雑な構造ですが、状態遷移ベースの計算モデルにはモノイド積がどうしても必要です。それでモノイド二重圏が登場するのですが、モノイド二重圏は3次元の圏の退化した姿だとみなせます。複数のモノイド積を導入したり、さらに別な結合演算を追加すると、次元と複雑さはさらに増します。しかし、精密な計算モデルを作るには高次元化は避けられないようです。