なぜ、どのように足し算が消失したのか：プランク定数の大惨事と生存者達

2008年から2010年くらいに、トロピカル代数や一元体F₁の話をよくしていました。今でもウッスラと興味は続いています。ずっと疑問に感じているのは、「一元体では、なぜ足し算がないのだろうか？」ということです。

「定義より足し算を持たない」と言ってしまえばそれでオシマイですが、なにかの根拠が欲しいのです。理論的な根拠じゃなくてもいいです、心情的な納得感があればそれでいいんです。

2010年当時に僕が考えた「納得のための理屈」は、「もともとはあった足し算が極限操作で死滅してしまった」というものです。しかし、完全に死滅したわけじゃなくて、一部の足し算が生き残っているように思えるのです。生き残ったヤツラが役立たずなので、足し算がないように見える、ということです。

この事情を、「いわゆる「一元体」の正体をちゃんと考えてみる」の「足し算はまったくないのだろうか」という節で次のように書いています。

[一元体F₁において] 足し算はまったく未定義なのでしょうか？次のように、0との足し算は認めてもいいような気がします（空欄は未定義）。

＋ 0 1

0 0 1

1 1

0 + x = x + 0 = x としてもヨサゲな状況証拠があります。確証がないので今日は書きません（僕の見当違いの可能性もあるし）。もっとも、0との足し算があっても大して役に立たないので、「ないも同様」かも知れませんけど。

「確証がないので今日は書きません」と書いてから4年以上経過した今、ちょっと書いておこうか、という気になりました。確証が見つかったわけではありません。もともとが空想（あるいは妄想）的な比喩で考えたことです。その空想を、事実や理論ではなくてファンタジーとして記すのも面白いかな、と。

内容：

連続と離散のあいだの空想的対応
非負実数の上にh-マスロフ和
ベクトル空間のp-ノルムと球
p-ノルムとh-マスロフ和
反脱量子化とカタストロフ
カタストロフの生存者達
だが不思議だ

連続と離散のあいだの空想的対応

僕の空想（あるいは妄想）的な比喩は、「僕がエフイチにハマる理由」に書いてあります。

マスロフのプランク定数を変動させると、3つの典型的な代数構造ができるわけです。それは、(R_≧0, ×, +), (R_≧0, ×, ∨), (R_≧0, ×) です。記号「∨」はmax演算の中置演算記号です。この3つは、F₂、B、F₁ の類似物ですよね。

プランク定数非負実数の代数系二元の代数系

h = 1 (R_≧0, ×, +) F₂

h = +0 (R_≧0, ×, ∨) B

h = +∞ (R_≧0, ×) F₁

どうやら、F₂、B、F₁ は離散有限、それも極小の有限におけるプランク定数 1, +0, +∞ の代数系みたいです。

この引用部分だけでは何だかワカンナイでしょう。

「マスロフのプランク定数」に関しては「マスロフ式算数がやたらに面白いんですけど」に説明してあります。hを正の実数として、次の演算を考えます。

(x^1/h + y^1/h)^h

これをxとyに対する二項演算と考えると、可換／結合的／掛け算に対して分配的となります。つまり、足し算と呼んでもよい二項演算なのです。なので僕は、h-マスロフ和と呼んでいます。パラメータhは、物理とのアナロジーから（マスロフの）プランク定数といいます。

大雑把に言えば、プランク定数hを1から0に変更して考えることが、マスロフ脱量子化（Maslov Dequantization）です。「マスロフ式算数がやたらに面白いんですけど」の「プランク定数と脱量子化」の節を引用すると：

プランク定数は物理で出てきますよね。僕は、物理のプランク定数が何であるか分からないのですが、マスロフは物理とのアナロジーで、マスロフ算数とその発展である脱量子化を構想したようです。
マソロフ脱量子化とその広大な応用分野を、要領よくまとめた報告である"MASLOV DEQUANTIZATION, IDEMPOTENT AND TROPICAL MATHEMATICS: A BRIEF INTRODUCTION"（http://glitvinov.googlepages.com/2007_JMS_426.pdf）に次の図が載っています。
予断から勘違いしやすのですが、この図では、普通の算数や数学（左上のTRADITIONAL MATHEMATICS）が物理の量子力学に対応しています。普通の計算は、既に量子化されているのです。普通の計算を脱量子化（古典化）することにより、「量子力学：古典力学＝普通の計算：？」の疑問符のところを埋めよう、という魂胆です。
脱量子化するために、パラメータh（プランク定数；kの逆数）を導入し、hが0に近づく極限（古典極限）を見よう、というわけです。h = 1 での計算が量子的計算であり、h = 0 での計算が脱量子的計算となります。既に見たように、「量子的足し算＝普通の足し算＝公平な足し算」であり、「脱量子的足し算＝max演算＝格差が究極的に拡大する足し算」です。

先に出した対応表（下に再掲）は、プランク定数の典型的な値で出現する連続な代数系に、離散版が対応するだろうということです。

プランク定数	非負実数の代数系	二元の代数系
h = 1	(R_≧0, ×, +)	F₂
h = +0	(R_≧0, ×, ∨)	B
h = +∞	(R_≧0, ×)	F₁

そもその、そんな対応があるのか？対応の法則は何か？と問われると正確に答えることはできません。要するに空想です。そんな対応があるような気がするだけです。仮にそんな対応があったとすれば、連続な代数系（非負実数の代数系）で起きた現象が、離散な代数系でも起きているかもしれない、そんな気がするのです。

非負実数の上にh-マスロフ和

今述べた連続と離散の対応は空想的なものですが、連続な代数系に関してはハッキリと述べることができます。

非負実数の全体をPと書きましょう。過去の記事ではR_≧0と書いていたものです。Positiveのつもりですが、0が含まれるので正確にはNon-negativeです。プランク定数h（h＞0）のマスロフ和を次のように書くことにします。

x $\oplus$ _h y := (x^1/h + y^1/h)^h

集合Pにh-マスロフ和 $\oplus$ _hを一緒に考えた代数系（可換モノイド）をP_hとします。

P_h = (P, $\oplus$ _h, 0)

プランク定数hの値が何であってもマスロフ和の中立元（零元）は0です。

h→0 と、プランク定数を0に近付けたとき、その極限でh-マスロフ和は大きい方を取る演算maxになります。x∨y = max{x, y} と書くと、この事情は次のように表現できます。

P₊₀ = (P, ∨, 0)

さて今回の問題は、h→∞ という方向の極限で、P_hがどのように変容するかです。直接考えても難しくはありませんが、視覚的に理解しやすいので、 p-ノルム（p乗平均ノルム）と関係づけることにします。

ベクトル空間のp-ノルムと球

次のWikipedia項目にp-ノルムの説明が詳しく載っています。

Lp空間 - Wikipedia

(x, y, z)∈R³ に関して、そのp-ノルム||(x, y, z)||_pは次のようになります。

(|x|^p + |y|^p + |z|^p)^1/p

p = 2 のときは普通のユークリッドノルムです。p = 1 が総和ノルム、p = ∞ は最大値ノルムとなります。ノルムが1であるベクトル達は単位球面を形成し、ノルムが1以下であるベクトル達は単位球体を形成します。1 ≦ p ≦ ∞ の範囲で、p-ノルムの球体（表面は球面）を描いた図があります。

（https://www.viz.tamu.edu/faculty/ergun/research/implicitmodeling/abstracts/sm99/index.html より）

pが1未満になると、球体が非凸になってしまうので考えないことが多いのですが、0 ＜ p ＜ 1 の範囲まで2次元で描いた図がありました。p-ノルムの円が色付きで表示されています。

（http://yaniv.leviathanonline.com/blog/math/out-of-the-norm/ より）

総和ノルムの円 -- 赤い菱型
ユークリッドノルムの円 -- 緑の普通の円
最大値ノルムの円 -- 一番外側の四角

赤い菱型の内側に入るへこんだ図形は、0 ＜ p ＜ 1 に対するノルム円となります。3次元のへこんだノルム球は次のようにひっこんでとんがった形です。

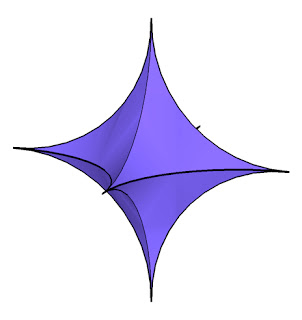
（http://nuit-blanche.blogspot.jp/2007/12/compressed-sensing-single-pixel-imaging.html より）

p-ノルムとh-マスロフ和

p-ノルムを、次元が2のとき、しかも第1象限だけで考えましょう。すると、p-ノルムは P×P→P という写像となります。第1象限だけなので、絶対値の記号は不要になり、(x, y)∈P×P に対するp-ノルムは、

(x^p + y^p)^1/p

となります。h := 1/p と置いてみれば、

(x^1/h + y^1/h)^h

そうです。h-マスロフ和と同じです。p-ノルムのべき乗pとh-マスロフ和のプランク定数hは、逆数の関係で移り合います。p-ノルムのpを0に近づけることは、プランク定数を無限大に飛ばしたときのマスロフ和を考えることと同じなのです。

先の 0 ＜ p ＜ 1 の範囲まで描いた2次元p-ノルムの図を眺めると分かるように、p→0 ではノルム円はx軸とy軸にひっついてしまいます。円板や球体の面積・体積は、p→0 の極限では消失します。p = 0 のときのノルム球まで3次元で描いた図もありました。

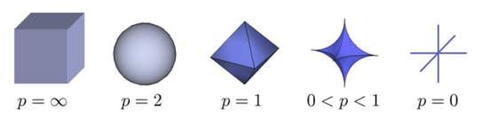
（http://m.blog.csdn.net/blog/lansatiankongxxc/13086711 より）

p = 0 では、それぞれの座標軸の絶対値1以下の部分しか残らないのです。第1象限だけを考えるなら、長さ1の線分が原点で接しているだけの図形になります。もとのベクトル空間の次元が何であれ、p = 0 では球が“線分の集まり”に退化してしまうのです。球面と球体の区別もなくなります。

h-マスロフ和 x $\oplus$ _h y = (x^1/h + y^1/h)^h に関しても、h→∞ で同じ現象が起きます。h-マスロフ和の定義域は、hが有限である限りは存在しますが、h = +∞ だと、p-ノルム球の場合と同様に1次元図形に崩壊してしまいます。 $\oplus$ _+∞ は、その定義のための土台を失うのです。

反脱量子化とカタストロフ

マスロフ達によれば、我々が普通に使っている算数・数学（Traditional Mathematics）が重ね合わせを基本にしていることから量子的であり、プランク定数が1の世界で計算しているのです。プランク定数を1から0へと極限操作して脱量子化を実行するわけです。

脱量子化した世界の足し算 x $\oplus$ ₊₀ y は、「xとyの大きい方」という意味です。プランク定数hが非常に小さいとき、(x^1/h + y^1/h)^h の括弧内は、非常に大きい数K（= 1/h）により、x^K + y^K と書けます。わずかでも x ＞ y であれば、x^K + y^K ≒ x^K となり、大きい方だけが選び出されることになります。演算 $\oplus$ ₊₀ は、わずかの格差も究極的に拡大する演算です。

h→∞ という操作は、h→0とは逆方向の極限をとるので反脱量子化とでも呼べばいいでしょうか。プランク定数を増大させて、足し算の変容を見るのです。プランク定数hが非常に大きいときは、x, yが0でないなら、x^1/hもy^1/hもほぼ1になります。したがって、x^1/h + y^1/h ≒ 2 となり、x $\oplus$ _h y ≒ 2^h です。足し算の結果に、xとyの値がほとんど影響を与えず、結果は巨大な数になります。

h ≒ 0 では格差が拡大されてしまうのに対して、hが大きいとxとyの差は無視されます。悪平等の世界とも言えるでしょう。もっと悪いことには、x $\oplus$ _+∞ y は、x ≠ 0、y ≠ 0 に対して発散して値を持てないことです。h = +0 では、なにはともあれ値がちゃんと確定していたのですが、h = +∞ では足し算 $\oplus$ _h が意味を失います。

0 ＜ h ＜ ∞ の範囲のプランク定数hに対するh-マスロフ和 $\oplus$ _h はP×Pで定義されます。h = +0 と脱量子化しても、定義域はP×Pのままでいられます。しかし、反脱量子化を実行すると、h-マスロフ和の定義域は、x軸とy軸を寄せ集めた1次元図形に縮退します。平面の領域が座標軸に吸引されて、最終的に完全に飲み込まれてしまいます。これはもうカタストロフ（大惨事）と言えるでしょう。陳腐な映画のシーンが思い浮かびます。

カタストロフの生存者達

プランク定数hが無限大のときのh-マスロフ和 $\oplus$ _+∞の定義域をハッキリとさせておきましょう。カタストロフの後でも、x軸／y軸は残るので、次の集合が $\oplus$ _+∞の定義域となります。

{(x, y)∈P×P | x = 0 または y = 0} = ({(x, 0)∈P×P | x∈P}∪{(0, y)∈P×P | y∈P})

要するに、第1象限のフチの所だけが残るのです。

y = 0 のときを考えると、x $\oplus$ _+∞ y = x $\oplus$ _+∞ 0 = lim_h→∞(x^1/h + 0^1/h)^h = lim_h→∞(x^1/h)^h = lim_h→∞x = x となり、プランク定数hの影響を逃れて値が定まります。

x $\oplus$ _+∞ y の定義をまとめると次のようになります。

0 $\oplus$ _+∞ 0 = 0
x ≠ 0 のとき x $\oplus$ _+∞ 0 = 0 $\oplus$ _+∞ x = x
x ≠ 0 かつ y ≠ 0 のとき x $\oplus$ _+∞ y は未定義

この $\oplus$ _+∞の定義の {0, 1}⊆P だけを抜き出すと：

＋	0	1
0	0	1
1	1

最初に挙げた「いわゆる「一元体」の正体をちゃんと考えてみる」の表が再現します。0との足し算は生き残っている、ということです。

プランク定数無限大のカタストロフで生き残った足し算は、まったく無意味のように見えます。しかし、僅かな意義は持っているみたいです。

$\oplus$ _+∞ の定義域は、Pの2つの直和を原点で接着した形をしています。これは、付点集合（pointed set）の圏における直和です。記号 $\amalg$ を使って、（ $\oplus$ _+∞の定義域） = P $\amalg$ P と書きましょう。圏の一般論から、直和には余対角（codiagonal）∇_P:(P $\amalg$ P)→P が存在します。カタストロフ後のマスロフ和 $\oplus$ _+∞ は、余対角 ∇_P に他なりません。

もし圏が双積を持つなら、余対角から足し算を構成できます。しかし残念ながら、付点集合の圏は双積を持ちません。わずかに残存した足し算の痕跡から、もとの豊かな足し算を再建する道はないのです。とはいえ、余対角∇_Pが足し算っぽい演算であるのは確かです。足し算の面影は残っていると言えるでしょう。

足し算再建のもうひとつ別な道として、Pに最初から∞を付け加えた P' = P∪{∞} を考えて、x $\oplus$ _+∞ y を次のように定義することです。ここで、xとyは0でも∞でもないとします。

＋	0	y	∞
0	0	y	∞
x	x	∞	∞
∞	∞	∞	∞

これは、P' ×P' →P' という形の写像になってはいます。ですが、無理やりな定義なので、なにがアリガタイのかはよく分かりません。再建とはいいながら、死人をゾンビにして頭数合わせただけのような気がします。

だが不思議だ

以上、「プランク定数が極限まで増大するという大惨事により、足し算が消失したのではないか」というストーリーでした。台集合がPのときは、このシナリオは事実になり得ると言っていいでしょう。しかし、離散的な二元集合である一元体F₁において、同じ大惨事が起きた証拠は何もありません。僕が夢想した「連続と離散のあいだの対応」を作る手がかりもありません。

それと、もっと不思議なのは、なんで掛け算は安定して存在しているのか？です。「「掛け算ありき」から見えるエキゾチックな世界と真実の世界」で述べたように、掛け算は足し算より基本的な演算とみなすこともできます。より基本的だから安定しているのでしょうか？プランク定数が縮小したり増大しても、掛け算は影響を受けないのでしょうか？なぜ？

たかが足し算、たかが掛け算、されど不思議なこと／謎なことが多いですね。