ボレルのパラドックス(あるいは、ボレル/コルモゴロフのパラドックス)と呼ばれる議論の簡易化したバージョンを紹介します。
問題と2つの解答
ダーツとかアーチェリーのマトを考えてください。次の図のようなものです。
水色の円の半径を1とします。赤い円の半径は1/3です。赤い所に矢が刺さると「当たり」だとします。矢がどこに刺さるかはまったくのランダムです。ただし、矢が水色の円の外に出ることはないとします。外に出ても無視して勘定に入れないと思ってもかまいません。
このとき、矢が赤い所に当たる確率はいくつでしょうか? というのが問題です。
解答例その1: 水色の円の面積は 1×1×π = π、赤い円の面積は 1/3×1/3×π = 1/9π だから、赤い円に矢が入る確率は 1/9。
解答例その2: 円は、中心から放射状に出る長さ1の線分が集まって構成される。どの線分に矢が刺さるかは同じ確率なので、1本の線分だけを考えれば十分。線分のなかで赤い部分は全体の1/3なので、赤い部分に矢が刺さる確率は1/3。
結果が違います。さて、どちらが正しいのでしょうか?
種明かし
どちらも間違いとは言えません。どちらが正しいと決定もできません。「矢がどこに刺さるかはまったくのランダムです」が曖昧な前提だからです。(前提をハッキリさせて、正誤を決めることもあります。)
確率分布(確率測度)がないと赤い円の確率の測りようがありません。この問題では確率分布が明示されてないので、解答者が各自で決めています。それぞれが想定した確率分布が違うので解答も違ってきます。矛盾があるわけではありません。つまり、擬似的なパラドックスなのです。
それぞれの確率分布を説明します。3000回矢を投げたとして、刺さった位置をシミュレートしてみます。まず解答例その1の前提は、円内の一様分布です。Rで次のようにすると、矢の跡が図になります。
require(ggplot2) N <- 3000 # 2倍のサンプルを作って、N個だけ使う a <- runif(N*2, -1, 1) b <- runif(N*2, -1, 1) mask <- a^2 + b^2 <= 1 x <- a[mask] y <- b[mask] x <- x[1:N] y <- y[1:N] qplot(x, y, alpha=I(0.5)) + xlim(-1, 1) + ylim(-1, 1)
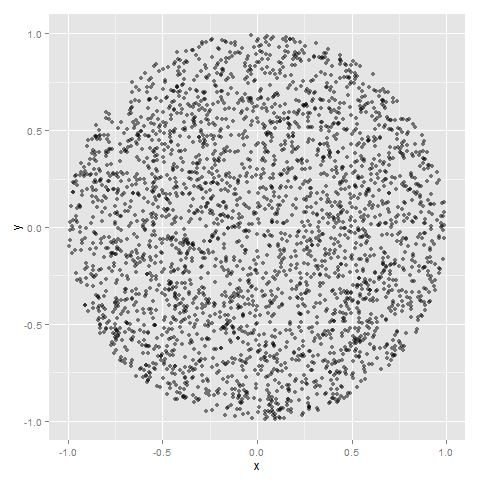
局所的なマダラはありますが、全体を眺めると、矢の跡は円内に一様に散らばっています。半径1/3の円内にある跡だけ抜き出して勘定してみます。そして、全体の跡(3000個)との比率を求めてみます。
hit <- x^2 + y^2 <= (1/3)^2 sum(hit)/N
sum(hit)/Nの値は0.1043333となり、確かに1/9(0.1111111)に近いです。
次は解答例その2のほう。こっちは、極座標で考えて、偏角t(0≦t≦2π)方向と半径r方向のどちらについても分布が一様だと仮定しています。
t <- runif(N, 0, 2*pi) r <- runif(N) qplot(t, r, alpha=I(0.5)) + xlim(0, 2*pi) + ylim(0, 1)
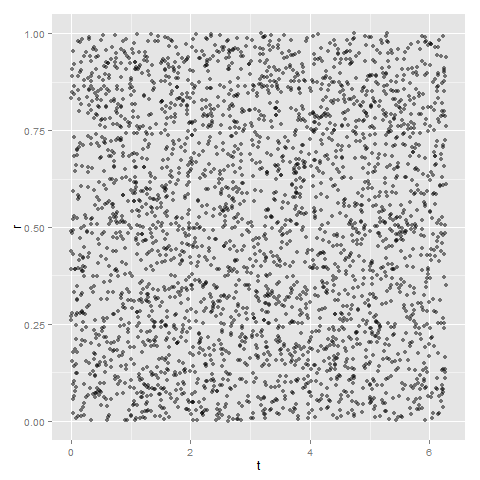
tとrの空間では、上の図のように矢の跡が一様に散らばります。このt-r空間での分布を、x = r*cos(t), y = r*sin(t) で、x-y空間に持って行くとどうなるでしょうか。先ほど定義したx, yを壊したくないので、x_, y_という変数を使って確かめます。
x_ <- r*cos(t) y_ <- r*sin(t) qplot(x_, y_, alpha=I(0.5)) + xlim(-1, 1) + ylim(-1, 1)
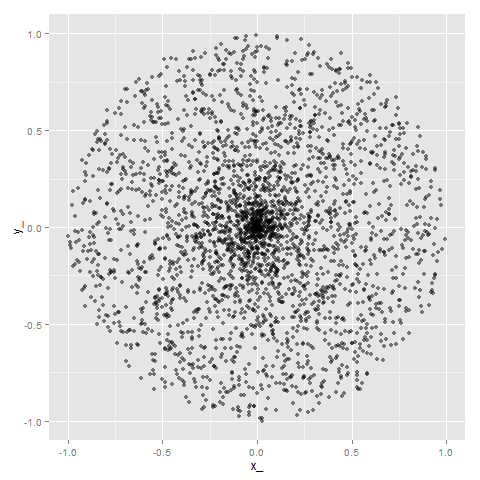
明らかに中心付近が濃くなっています。半径1/3の赤い円=当たり領域に入る跡の比率は:
hit_ <- x_^2 + y_^2 <= (1/3)^2 sum(hit_)/N
値は0.3486667で、1/3(0.3333333)に近いです。
円の中心が濃くなるのは何故でしょう; t-r空間で短冊のような細長い長方形を考えてみます。
t1 <- t[t <= 0.5] r1 <- r[t <= 0.5] qplot(t1, r1, alpha=I(0.5)) + xlim(0, 2*pi) + ylim(0, 1)
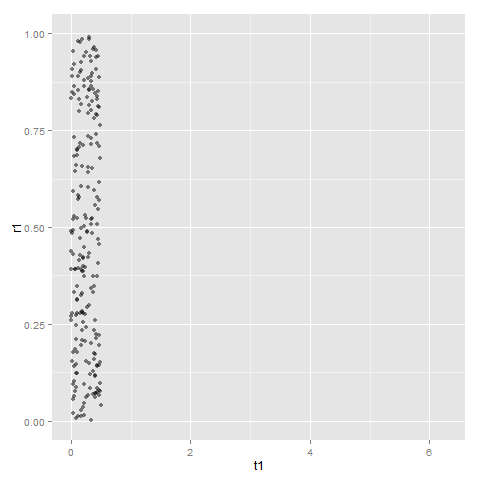
(t, r)|→(x_, y_) という変換で、短冊の上のほうは広がって、逆に下のほうはギュッと縮まって扇型になります。扇型のトガッたほうでは、もとの分布が圧縮されて濃くなるのです。
x1 <- r1*cos(t1) y1 <- r1*sin(t1) qplot(x1, y1, alpha=I(0.5)) + xlim(-1, 1) + ylim(-1, 1)
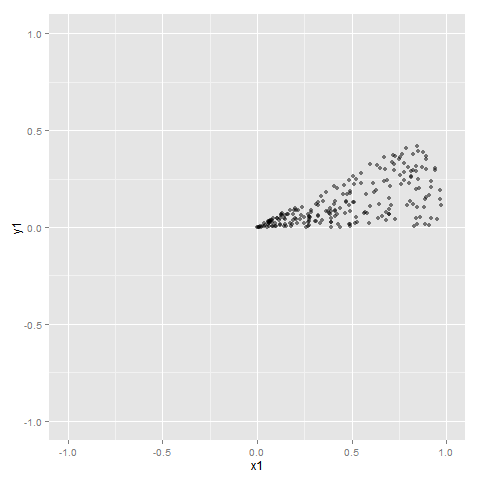
円の中心で密度の値が立ち上がっているのを見るために、3次元グラフを描いてみます。
d <- 0.05 K <- 1/d n <- floor(x_ / d) m <- floor(y_ / d) n <- n + K + 1 m <- m + K + 1 z <- matrix(0, 2*K, 2*K) for (i in 1:N) z[n[i], m[i]] <- z[n[i], m[i]] + 1 xBreaks <- seq(-1, (1 - d), d) + d/2 yBreaks <- xBreaks persp(xBreaks, yBreaks, z, xlab = "x", ylab = "y", zlab = "z", xlim = c(-1, 1), ylim = c(-1, 1), theta = 30, phi = 30, expand = 0.5, col = "skyblue")
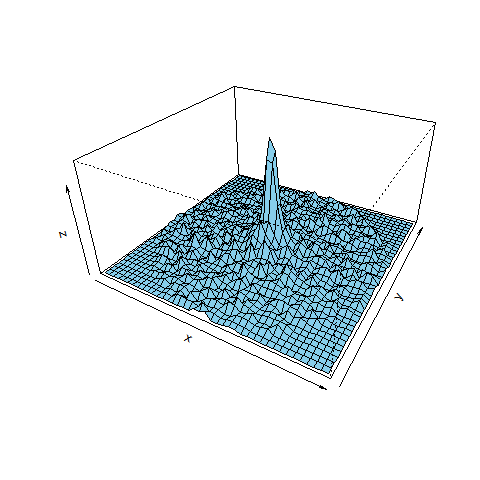
軟化処理をしてないのでクチャクチャですが、円の中心で密度が急激に増大しているのは見てとれるでしょう。
まとめ
- 確率分布(確率測度)を決めないと、確率を云々することは出来ません。
- Rでシミュレーションすると分かりやすいですね。
[追記]
解答例その2がおかしいと思う方、次ならどうなんでしょうか。
問題: 辺の長さが1の正方形のマトで、矢が赤い所に当たる確率はいくつでしょうか?

解答例: 正方形は、縦に走る長さ1の線分が集まって構成される。どの線分に矢が刺さるかは同じ確率なので、1本の線分だけを考えれば十分。線分のなかで赤い部分は全体の1/3なので、赤い部分に矢が刺さる確率は1/3。
[追記その2]
マトの形が次のようだったら、「線の集まり」論法が使える? それとも使えない?
