ベルトラン／ボレルのパラドックスから見える確率の本音と建前

「簡易版・ボレルのパラドックスとその解釈：R言語を使って」のコメント欄にて、id:hokuto-heiさんにベルトランのパラドックスを教えていただきました。ベルトランのパラドックスは、hokuto-heiさんのエントリーにもWikipediaにも詳しく載っています。

ボレルのパラドックスもベルトランのパラドックスも、同一の確率的枠組み（測度は未定）に、異なる確率分布（具体的な測度）をいくらでも作れて、それらのどれも「原理的な部分で否定する理由は全くない」（by hokuto-hei）という趣旨です。

パラドックス（逆説）という名前は付いてますが、実際はパラドックスではないので、以下、ベルトラン問題、ボレル問題と呼ぶことにします。ここでのボレル問題は、オリジナルである球面上の大円に関するものではなくて、僕が簡易化した円板に関するものです。

ベルトラン／ボレルの問題を調べてみてしみじみと感じた事は、オフィシャル・フォーマルな確率空間の定義と、実際の測度計算とのあいだのギャップです。このギャップを丁寧に説明しないことが、奇妙な誤解や思い込みを生む原因となっていると思います。徹底的にギャップを埋めます。

内容：

確率分布
おおもとの確率空間
測度の引戻し
ベルトラン問題・分布1の構成
- 補足的注意：おおもとの確率空間に対する気持ち
ベルトラン問題・分布1の言い換え
ベルトラン問題・分布2の構成
「弦の長さ」という確率変数
擬似パラドックスの構造
おおもとの確率空間の必要性

確率分布

ベルトラン問題において、円の半径を1に固定して考えれば、「円の弦が√3より長くなる確率」を求める問題としていいので、内接三角形には言及しません。いろいろある確率の与え方のなかで、次の2つだけを取り上げます。（分布は確率分布のことで、確率分布は確率測度とニュアンスを除いて同義です。）

分布1：弦の一端を固定して、他端を円周上の任意の点にとる。確率分布は円周上で一様。
分布2：弦の中点を、円板内の任意の点にとる。確率分布は円板内で一様。

簡易ボレル問題での確率分布は：

分布1 ：円板内で、デカルト座標に関して一様
分布2 ：円板内で、極座標に関して一様

これから登場する集合に名前を付けておきます。

C = Circle = {(x, y)∈R² | x² + y² = 0}
D = Disk = {(x, y)∈R² | x² + y² ≦ 0}
P = PolarCoord = {(r, t)∈R² | 0 ≦ r ≦ 1, 0 ≦ t < 2π} （単位円の内部のみ）

平面内の円周Cとは別に、次のSを導入しておきます。

S = R/2πZ = (差が2πである実数を同一視した加法群)

Sの要素は、0 ≦ θ < 2π である実数で表現できるので、Sの要素を実数θを使って表すことにします。ただし、足し算などで 0 ≦ θ < 2π を飛び出したら適宜調整します。

以上の記号の約束のもとで、ベルトラン問題、簡易ボレル問題における確率分布の概要は：

	もとになる一様分布を置く空間	確率分布を与える空間	備考
ベルトラン問題・分布1	S	C	SとCは同型
ベルトラン問題・分布2	D	D	一様分布をそのまま使う
ボレル問題・分布1	D	D	一様分布をそのまま使う
ボレル問題・分布2	P	D	PからDに分布を前送り

詳細はこれから述べます。

おおもとの確率空間

「「分布、測度、密度」は同じか違うか」へのBackさんのコメントに、

確率や統計の教科書でどうして確率空間への言及が（あまり）されないか、想像に過ぎないのですが「確率空間そのものには興味が無いから」に尽きるのではないかと思います。

とありましたが、そのとおりだと思います。通常、確率変数の定義域である確率空間は明示的に出す必要はありません。

多くの場合、おおもとの確率空間なんて必要なくて、確率変数（可測写像）の値の空間上の確率分布（通常は密度関数から構成される測度）があればこと足ります。確率変数とは可測写像だとするオフィシャルな立場では、おおもとの確率空間がないと確率変数もあり得ないので、建前上「あることにする」だけです。

建前を律儀に押し通すなら、おおもとの確率空間を作らねばなりません。実際にやってみると、「確率空間ありき」はかなり空疎な建前で、想定された確率変数の「値の空間上の分布」から逆向きに測度を作るという、なんだか虚しい作業になります。（だから、みんなやらないのでしょう。）

それでもなお、おおもとになる確率空間を作ってみます。今回だけだけど。

簡易ボレル問題に関して必要な作業はやたら簡単で「簡易版・ボレルのパラドックスとその解釈：R言語を使って」で述べているので、ベルトラン問題について述べます。

ベルトラン問題で確率を与えるべき対象物（根本事象）は弦なので、弦の全体からなる集合を考えます。弦は、円周C上の2点で決定されるので、「弦の全体」はC×Cと考えていいでしょう。C $\stackrel{\sim}{=}$ S なので、S×Sに移って、S×Sの点を 0 ≦ θ₁ ＜ 2π、0 ≦ θ₂ ＜ 2π である実数の組 (θ₁, θ₂) で表します。

C×CでもS×Sでも同じことですが、(θ₁, θ₂) という表示を使うので、ベルトラン問題の確率空間の台集合（根本事象の集合）はS×Sだと約束します。

S×Sは、図形としてはトーラス（ドーナツや浮き輪の表面の形）ですが、R³に埋め込んだりはしません。トーラスS×Sの点には、0 ≦ θ₁, θ₂ ＜ 2π であるペア (θ₁, θ₂) を通じてアクセスします。

さて、S×S上にどんな確率空間を構成するか？これは事前に決めることができなくて、確率測度はもちろん、可測構造（σ代数）さえも状況に応じて構成するしかないのです。確率空間は所与のものというより、その場その場で設定するものです -- とはいえ、一番最後の段落も参照。

測度の引戻し

可測写像 f:A→B があるとき、A上の測度をfに沿ってB上に前送り（push-forward）してB上の測度を作ることは非常によく行われます。「分布」のオフィシャルな定義は、そのような前送りで作られた像測度（image measure）のことです。

おおもとの確率空間を後付けで構成するときに使える手段は、測度の引き戻し（pull-back）しかないでしょう。と、そう思いますが、引き戻し構成をちゃんと把握しているわけじゃないです。f:A→B が可測写像で、ΣA、ΣB がσ代数とします。ΣAが、fによるΣBの逆像で生成されるなら、B上の測度νをA上に持って来ることができるでしょう、たぶん。作られたA上の測度を μ = f^*(ν) とすると：

μ(f^-1(Y)) = ν(Y)

X = f^-1(Y) の形の集合Xに対しては上記のようにμ(X)を定義して、その定義をΣA全体に拡張します。この拡張が無条件にいつでも出来るわけではないので、引き戻しは出来る場合に限り使えるだけです（前送りはいつでも出来ます）。引き戻しによりμが作れれば、f_*(μ) = ν （μの前送りがν）となります。

Aが可測空間でさえなくて単なる集合のとき、B上のσ代数ΣBを引き戻してA上のσ代数ΣAを（事後的に）作ることが出来ます。Y∈ΣB に対する X = f^-1(Y) の形の集合Xを基底にしてσ代数を生成します。これは、fを可測にする最小のσ代数です。

上記2つの方法を組み合わせると、Bが測度空間 B =(B, ΣB, ν) のとき、単なる集合Aからの単なる写像 f:A→B に対して、A上の測度空間を誘導（induce）することが出来ます（おそらく）。そして、あたかも最初からAが測度空間であったようなフリをするわけです。

「そんなことして何がうれしいの？」という心情的疑問は残りますが、その答はおそらく「オフィシャル・フォーマルな定義を守るため」でしょう。オフィシャル・フォーマルな定義に拘らないなら、引き戻し構成はたいてい不要だと思います。今回は拘ります！ 律儀に引き戻し測度を構成します。

ベルトラン問題・分布1の構成

弦の全体を表すトーラスS×S上に確率空間を構成します。分かりにくかったら、次節と比較して理解するといいと思います。写像 d:S×S→S （dはdifference）を使って、S上の測度構造をS×Sに引き戻します。d:S×S→S は次の定義です。

d(θ₁, θ₂) = θ₂ - θ₁

S = R/2πZ は加法群なので引き算が定義できます。マイナスはその引き算のことです。ただし、0 ≦ θ₁, θ₂ ＜ 2π の範囲内で表すときには絶対値が必要です。

d(θ₁, θ₂) = |θ₂ - θ₁|

Rで3次元プロットを描いておきます。

d <- function(theta1, theta2) {
    abs(theta2 - theta1)
}

N <- 100
# 0から2πまでをN等分したメッシュを作る
x <- seq(0, 2*pi, by=(2*pi / N))
y <- x
# プロット用にz値の行列を作成する
z <- outer(x, y, d)

# 3Dプロット
persp(x, y, z,
      xlab = "θ1", ylab = "θ2", zlab = "|θ2 - θ1|",
      xlim = c(0, 2*pi), ylim = c(0, 2*pi), zlim = c(0, 2*pi),
      theta = 10, phi = 20, expand = 0.7, col = "skyblue")

S上の区間 {φ∈S | a ≦ φ ＜ b} に対して、その測度を (b - a)/2π で定義します。S $\stackrel{\sim}{=}$ C なので、この測度は円周C上の一様な分布の表現ともみなします。d:S×S→S によって、S（Cでも同じ）上の区間の逆像を作ると、トーラス上の“斜めの帯”ができます。斜め帯の測度は、(対応する円周上の区間幅÷2π) で与えられます。

以下は、{φ∈S | π/2 ≦ φ ＜ π} に対応する斜め帯の図です。これは、{(θ₁, θ₂)∈S×S | π/2 ≦ θ₂ - θ₁ ＜ π} により定義されるトーラス上の領域（の展開図）です。

S×S上の測度構造は次のようになります。

台集合： S×S
σ代数： S上の区間をdで引き戻した“斜め帯”集合から生成されるσ代数
測度：“斜め帯”に対して、 (対応する円周上の区間幅÷2π) を割り当てる

補足的注意：おおもとの確率空間に対する気持ち

弦の空間のような所に、引き戻しで測度を入れている例を見たことがありません。その理由は、確率空間を作っても別にメリットがないからでしょう。実際の計算はS（Cでも同じ）上で行うのですから。

もうひとつの考え方は、「おおもとの確率空間は作らなくても最初からある」とするものです。S×Sと同型な空間Uがあり、(U, ΣU, μ) が最初から揃っているとします。ただし我々は、ΣUやμの詳細は知らず、Uからの可測写像で前送りされた像測度であるS上の分布しか見えてなない、と考えます。

この発想だと、μ(f^-1(Y)) = ν(Y) という等式は引き戻し測度の定義ではなくて、おおもとの測度μに対する仮定を述べていることになります。

どう考えようとも、実際的な確率計算に影響はありませんが、「気の持ちよう」には、次の2種類があるように思えます。

おおもとの確率空間は、人間がその場その場で設定（構成）するもの。
おおもとの確率空間は所与のものだが、人間には未知なので、その場その場で想定（条件付け）をする。

どっちがいいかは分かりません（一番最後の段落も参照）。が、2番目の立場では、おおもとの確率空間を構成する責任は人間じゃなくて神様にあるので、責任転嫁できます。

ベルトラン問題・分布1の言い換え

トーラスS×S上の確率空間の構成は、ややこしいですね。代わりに通常使われる方法は、幾何的な操作を使う方法です。

「円周C上に2点を選ぶ」ということを、最初の1点を固定して（例えば点(1, 0)にします）、残りの1点を円周上から選ぶことだと言い換えます。そうすると、円周C上の残りの点に対応するS上での位置（偏角）φだけで「2点の組＝弦」を指定できます。本来の2点の位置（偏角）を θ₁, θ₂とすると、1点目を(0, 1)に固定した残りの点の位置φは φ = θ₂ - θ₁ となります。（絶対値付けるかどうかは表示と計算上の問題。）

「2点の組＝弦」を1点だけの位置へと自由度を落とす操作が、(θ₁, θ₂) |→ θ₂ - θ₁ という写像に対応します。弦に関する確率を、円周C上の一様な分布で測ろうとすることは、円周Cと同型なS上の一様測度を、弦の空間（トーラスS×S)に引き戻していることになります。

これは、本来測るべき「弦に関する確率」を「円周上の点に関する確率」に置き換えているわけです。そして、「弦の空間上の確率分布」を「円周上の一様分布」で代用していることでもあります。確率の計算は、結局「円周上の一様分布」で行うので、しちめんどくさい「弦の空間上の確率分布（測度）」を構成する意味はたいしてないのです。

ただし、「おおもとになる確率空間はどこにあるの？」と聞かれれば、それは円周上にあるのではなくて、弦の空間であるトーラスS×S上にある、と答えるべきです。

ベルトラン問題・分布2の構成

次は分布2をトーラスS×S上に構成します。話の流れは分布1と同じです。写像 c:S×S→D （cはcenter）を使って、円板D上の測度を引き戻します。

c(θ₁, θ₂) = ((cos θ₁ + cos θ₂)/2, (sin θ₁ + sin θ₂)/2)

「θ₁, θ₂ により決まる円周C上の2点」の中点が c(θ₁, θ₂) です。この写像cを調べても確率の扱いに関して利するところは何もありませんが、確率空間の実感を得るために図示してみます。

必要な値を先に計算します。

N <- 20
M <- N*3
th1Breaks <- seq(0, 2*pi, (2*pi)/N) # 縦方向の線群 荒い
th2Breaks <- seq(0, 2*pi, (2*pi)/M) # 横方向の線群 細かい

cX <- function(theta1, theta2) (cos(theta1) + cos(theta2))/2
cY <- function(theta1, theta2) (sin(theta1) + sin(theta2))/2

xValMatrix <- outer(th1Breaks, th2Breaks, cX)
yValMatrix <- outer(th1Breaks, th2Breaks, cY)

θ₁-θ₂空間（横方向にθ₁軸）にメッシュを描いておきます。方眼の縦方向と横方向で色と目の粗さを変えています。

for (i in 1:(N + 1))
     grid.lines(c(th1Breaks[i]/(2*pi), th1Breaks[i]/(2*pi)), c(0, 1), gp = gpar(col="red"))
for (j in 1:(M + 1))
     grid.lines(c(0, 1), c(th2Breaks[j]/(2*pi), th2Breaks[j]/(2*pi)), gp = gpar(col="blue"))

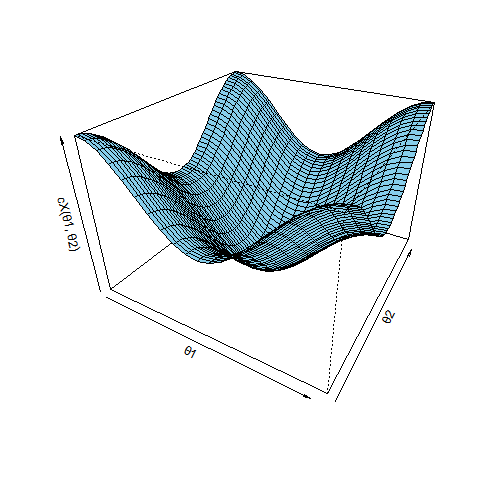
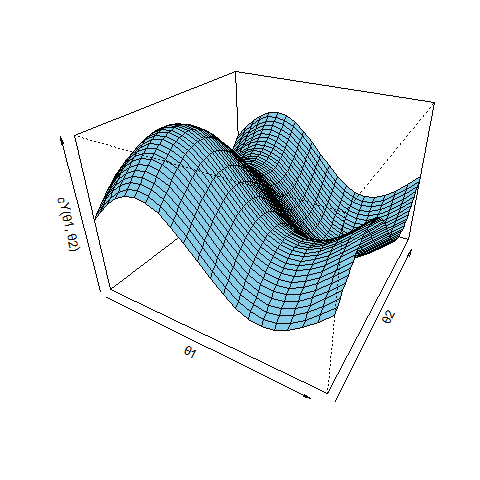
写像cは c:(θ₁, θ₂)|→(x, y) ですが、cX:(θ₁, θ₂)|→x、cY:(θ₁, θ₂)|→y に分けて3Dプロットを2つ描くと次のよう。

persp(th1Breaks, th2Breaks, xValMatrix,
      xlab = "θ1", ylab = "θ2", zlab = "cX(θ1, θ2)",
      xlim = c(0, 2*pi), ylim = c(0, 2*pi), zlim = c(-1, 1),
      theta = 30, phi = 30, expand = 0.7, col = "skyblue")

persp(th1Breaks, th2Breaks, yValMatrix,
      xlab = "θ1", ylab = "θ2", zlab = "cY(θ1, θ2)",
      xlim = c(0, 2*pi), ylim = c(0, 2*pi), zlim = c(-1, 1),
      theta = 30, phi = 30, expand = 0.7, col = "skyblue")

θ₁-θ₂空間のメッシュに写像cを適用すると、写像先のx-y空間の円内に次のような模様が描かれます。

for (i in 1:(N + 1))
     grid.lines(xValMatrix[i,]*0.5 + 0.5, yValMatrix[i,]*0.5 + 0.5, gp = gpar(col="red"))
for (j in 1:(M + 1))
     grid.lines(xValMatrix[,j]*0.5 + 0.5, yValMatrix[,j]*0.5 + 0.5, gp = gpar(col="blue"))

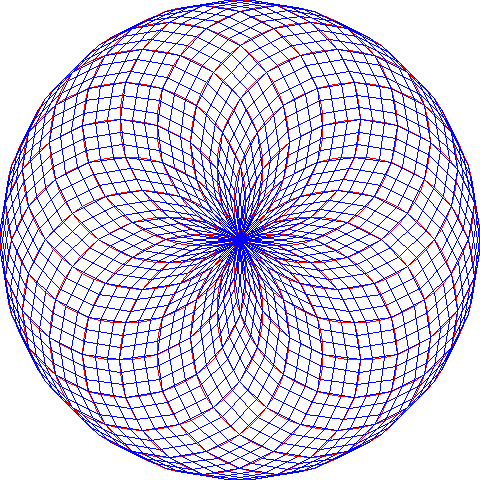
写像cによりトーラスが円板内に押し込まれるのですが、目を細めて無の境地で眺めると、ホラッ、円盤内にトーラスの形が見えてくるでしょう。

見えませんか？では悪乗りしてもうひとつ。矩形としてのθ₁-θ₂空間に、細長い緑の帯があったとすると、それはトーラス上の幅付きリングになります。その緑のリングは写像cにより円板内に押しつぶされて貼り付けられます。

for (i in 1:(N + 1))
     grid.lines(xValMatrix[i,]*0.5 + 0.5, yValMatrix[i,]*0.5 + 0.5, gp = gpar(col="red"))

w <- (2*pi)/N # 帯の幅
th1Breaks2 <- seq(0, 2*pi, (2*pi)/N) # 縦方向の線群 荒い
th2Breaks2 <- seq(0, pi + w, w/N) # 横方向の線群 一部だけ、とても細かい

xValMatrix2 <- outer(th1Breaks2, th2Breaks2, cX)
yValMatrix2 <- outer(th1Breaks2, th2Breaks2, cY)

for (j in 1:(N + 1))
     grid.lines(xValMatrix2[,j]*0.5 + 0.5, yValMatrix2[,j]*0.5 + 0.5, gp = gpar(col="green"))

と、こんなことはどうでもよくて、問題は、写像 c:S×S→D により、円板D上の測度が引き戻されて、S×S上の測度を定義することでした。このとき円板Dには、外側のR²の標準測度（ボレルσ代数とルベグ測度）と同じ測度を考えます。

建前としては、トーラス（弦の空間）S×Sの部分集合（事象）の測度を引き戻し測度で測ることになります。実際にはもちろん、円板Dとその部分集合しか見ません。毎度トーラスを意識する人はいないでしょう。

「弦の長さ」という確率変数

ここで扱っている「弦」とは、単位円周上の2点を両端とする線分です。その弦は、トーラスS×Sの1点で表現されるので、「弦の空間＝トーラス」とみなしたのでした。

弦の長さをLとすると、Lは弦の空間からR（実数）への写像となります； L:S×S→R。S×Sにはなんらかの可測構造があるとして、Lは可測写像とします。するとLは、オフィシャルな意味での確率変数です。ベルトラン問題を、よく使われる記法で書くと、「確率 P(L ≧ √3) を求めなさい」となります。

Lを (θ₁, θ₂) で書くと、次のようになります。

$\newcommand{\abs}[1]{|#1|} L(\theta_1, \theta_2) = \sqrt{2 - 2\cos (\abs{\theta_2 - \theta_1})}$

円周S（Cと同じ）を走る変数φと、円板Dを走る変数 (x, y) による表示も求めておきます。絵を描くか、三角関数の計算かで求まります。

空間	変数	弦の長さの表示
S×S	(θ₁, θ₂)	$L(\theta_1, \theta_2) = \sqrt{2 - 2\cos (\abs{\theta_2 - \theta_1})}$
S	φ	$L_S(\phi) = \sqrt{2 - 2\cos (\phi)}$
D	(x, y)	$L_D(x, y) = 2\sqrt{1 - x^2 - y^2}$

変数のあいだの関係：

$\phi = |\theta_2 - \theta_1|$
$x = \frac{\cos (\theta_1) + \cos (\theta_2)}{2}, \: y = \frac{\sin (\theta_1) + \sin (\theta_2)}{2}$

本来であれば、確率変数 L:S×S→R に対して、区間[√3, 2]の逆像 L^-1([√3, 2]) を求めて、その測度をS×S上の測度で測るべきです。しかし実際には、次のどちらかで P(L ≧ √3) を求めています。

確率変数 L_S:S→R に対して、逆像 L_S^-1([√3, 2]) の測度を、S上の一様測度で測る。
確率変数 L_D:D→R に対して、逆像 L_D^-1([√3, 2]) の測度を、D上の一様測度で測る。

計算してみると、この2つの値は違います。

L_S ≧ √3 からは、cos(φ) ≦ -1/2 が出て、 π/3 ≦ φ ≦ 2π/3、当該の確率は 1/3。
L_D ≧ √3 からは、x² + y² ≦ 1/2 が出て、 当該の確率は 1/4。

擬似パラドックスの構造

「弦の長さ」である確率変数 L:S×S→R は具体的に与えられます。Lが√3以上である確率、つまり P(L ≧ √3) も意味を持ちそうです。L = d;L_S = c;L_D も間違いありません。となると、P(L ≧ √3) = P(L_S ≧ √3) = P(L_D ≧ √3) を期待してしまいます。しかし実際は、P(L_S ≧ √3) と P(L_D ≧ √3) はまったく違う場所で計算されているので一致する保証なんてない、ということです。

この事実をパラドックスと感じてしまう心理は次のようなものでしょう。

所与の確率空間があり、そこで確率が一意的に計算できるはずだ。
計算に都合がよい2つの空間と2つの分布で計算したら結果が違う。
一意的な値のはずが、そうではない。矛盾だ。

結論を言えば、確率分布（測度）を定義（構成または条件付け）する前に、所与の確率空間なんてものはなく、一意的な値の求めようもない、ということです。そして、冒頭で言ったように、同一の確率的枠組み（測度は未定）に、異なる確率分布（具体的な測度）をいくらでも作れるのです。

簡易ボレル問題も同じ構造で、円板D上の分布を2種類の方法で定義しています。

	根本事象の空間	一様分布を置く空間
ベルトラン問題・分布1	S×S	S（Cと同型）
ベルトラン問題・分布2	S×S	D
ボレル問題・分布1	D	D
ボレル問題・分布2	D	P

確率の計算は「一様分布を置く空間」で行われます。分布を一様分布に限る必要は全然ありませんが、計算が簡単で理解しやすいので選ばれています。

こうして比べると、簡易ボレル問題は簡単にし過ぎたきらいはあります。

ベルトラン問題の「弦の空間」は目に見えないが、簡易ボレル問題の「点の空間＝マト」は直接目に見えている。
ベルトラン問題では確率変数Lにより事象を定義するが、簡易ボレル問題では直接的にマトの部分集合で事象を定義する。
ベルトラン問題では分布1も分布2も非自明な写像（dとc）と関係しているが、簡易ボレル問題の分布1は写像を経由しない。

単純化し過ぎてメッセージが伝わらなかった、と言えます。

おおもとの確率空間の必要性

ベルトラン問題の円周Sと円板Dは、計算に使った一様測度を添えれば、それ自体で確率空間です。簡易ボレル問題の極座標の空間Pも、その意味では完結した確率空間となります。確率変数の値の側は、いつだって像測度で確率空間です。

なので、ベルトラン問題・分布1でトーラスS×Sを一切出さずに円周S上でだけ考えても、ちゃんと確率空間の枠内で計算していることになります。この点はクリアです。

クリアじゃないのは、現象のモデルとして最初に想定された「おおもとの確率空間」の扱いです。ベルトラン問題で言えば弦の空間であるトーラスの扱いです。通常「おおもとの確率空間」は捉えどころがなく、イメージするのが難しいものです。たいてい、計算にも使えません。

僕の短い経験（ココラから）と個人的感想では、おおもとの確率空間での話か、計算に使う空間の話か判読できないのは負担に感じます。「このXは、いったいどこのXだよ!?」「変数なの関数なの？それとも定数かい？」という感じ。ハッキリと書いてほしいな、と希望。

最後に、おおもとの確率空間に対する“感覚”の話：なんだかんだと言っても、やっぱりおおもとの確率空間は所与で、そこに一意的なThe・確率があるんじゃないか、という感覚。この感覚は拭い切れないですよね。というか、自然現象をモデル化する際には、そう考えるしかないでしょう。想定する確率空間は人が構成するが、それはThe・確率と比較するためのもんだ、という位置づけ。

モデルは実在か仮構か？なんて議論に深入りするつもりはないので、この辺で。