テンパリー／リーブ圏とカウフマンのスケイン関係式 - 檜山正幸のキマイラ飼育記 (はてなBlog)

だいぶむかし -- 2008年6月、テンパリー／リーブ代数を話題にしたことがあります。

テンパリー／リーブ代数への最初の言及は2006年かな↓

行列のトレースの性質をやっと納得

明日（2016年勤労感謝の日）、テンパリー／リーブ圏の話をする機会があるので、昔を思い出してちょっと計算してみました。2008年の計算の続きと整理みたいなものです。予備知識に関しては、2008年当時のid:hiroki_fさんによる解説があります。

Temperley-Lieb Algebraのtraceについて。

時間がなかったので、様子見の計算をチョロチョロしただけですが、だいたいの様子を記しておきます。

内容：

言葉と記法
カウフマン圏
圏の線形化
イデアルによる商線形圏
テンパリー／リーブ圏の構成
ブレイド図の圏
カウフマンのスケイン関係式
ブレイド図の圏の線形表現
スケイン関係式とライデマイスター／アルチン同値関係
計算結果の解釈

言葉と記法

しばしばテンパリー／リーブ図（Temperley-Lieb diagram）と呼ばれる“あのテの図”を、ここではカウフマン図（Kauffman diagram）と呼びます。図式的な表現をはじめたのはカウフマンだからです。「あのテの図」に関しては、冒頭に挙げた過去記事参照。
カウフマン図の輪をサークル（円）と呼びます。（ループと呼ぶことが多いです。）
カウフマン図のサークルはスカラーに置き換えて計算しますが、そのスカラーをサークル乗数と呼ぶことにします。（以前はループ乗数と呼んでいました。ループ変数とかループ因子と呼ぶこともあるようです。）
kが可換体*1で、δ∈k として、δをサークル乗数とするテンパリー／リーブ圏（Temperley-Lieb category）をTL_{(k, δ)}と書きます。可換体（スカラー体）kが了解済みならTL_δと略記します。さらにδも了解済みなら単にTLと書きます。
ここでは、サークル乗数δをパラメータとしてTL_δと書きますが、サークル乗数とは別なパラメータを使うこともあるので注意してください。
テンパリー／リーブ圏TLのエンドセットTL(n, n)は、圏の結合を乗法とする代数（多元環）となるので、これをテンパリー／リーブ代数（Temperley-Lieb algebra）と呼びます。TLA(n) := TL(n, n) とします。ひとつのテンパリー／リーブ圏内に、n = 0, 1, 2, ... でパラメトライズされた可算無限個のテンパリー／リーブ代数TLA(n)が含まれます。

今回は、係数を複素数（k = C）として、「1の三乗根ω」を使った“カウフマンのスケイン関係式”を計算で確認します。

テンパリー／リーブ圏TL_{(k, δ)}を定義するために、事前にカウフマン圏という圏を定義して、カウフマン圏の複素線形化として目的のテンパリー／リーブ圏を構成することにします。

カウフマン圏

M = (M, ・, e) をモノイドとします。M上の対合（involution）とは、次の性質を持つ写像 (-)^-:M→M のことです。

(a^-)^- = a
(a・b)^- = b^-・a^-
e^- = e

Mが可換モノイドなら、(a・b)^- = a^-・b^- でもかまいません。Z = (Z, +, 0) に対して、n^- := -n とすると対合になります。C_×を0を除いた複素数として、C_× = (C_×, ・（掛け算）, 1) とすると、z^- = (1/zの共役) は対合になります。C_×の場合、共役だけ／逆数だけでも対合になりますし、z^- = z でも対合です。

以下、M = (M, ・, e, (-)^-) は対合を持つ可換モノイドとします。今後は、Mの要素をギリシャ文字で書くことにします。

カウフマン図は上から下に向かって描き、カウフマン図の結合は、上下に並べて表現します。カウフマン図KとLのこの順での結合をK;Lで表します。カウフマン図の結合の具体例を次に挙げます。

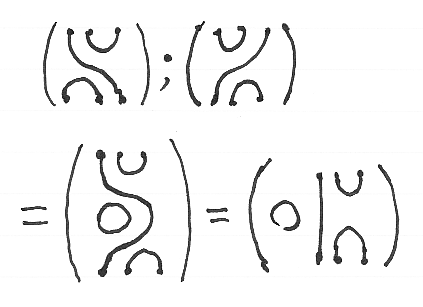
モノイドMの要素δを選んで固定します。このδはサークル乗数です。モノイドMの任意の要素αとカウフマン図Kの組(α, K)を考えます。Kがサークルを持つとき、Kからサークルを1個取り除いたカウフマン図をK'とします。このとき、(α, K)と(αδ, K')は同値だとします。この同値関係*2で割った商集合を考えて、(α, K)を含む同値類を単にαKと書きます。商集合のなかでは、同値関係がイコールになるので：

αK = (αδ)K'

特に、

K = 1K = (1δ)K' = δK'

下に、サークルを乗数δに直す具体例を挙げます。

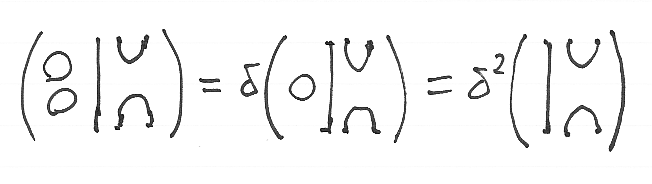
αKの形のカウフマン図をM-係数付きカウフマン図と呼びましょう。上記の定義から、“図Kのなかのサークル”と“係数αに含まれるδ因子”は相互に変換可能です。

δをサークル乗数とするM-係数付きカウフマン図を射とする圏をKauf_{(M, δ)}と書いて、（M-係数の）カウフマン圏（Kauffman category）と呼ぶことにします。カウフマン圏の対象類は、自然数の全体 {0, 1, 2, ...} です。カウフマン圏のエンドセットはカウフマン・モノイド（Kauffman monoid）です。

カウフマン圏では、2つのカウフマン図を左右に並べることでモノイド積（テンソル積）を入れられます。空なカウフマン図がモノイド単位です。また、カウフマン図を180度回転することで双対を定義します。結合／モノイド積／双対と、M-係数のスカラー乗法との関係は次のようです。モノイド積を $\otimes$ 、双対を(-)^*で表しています。

(αK);(βL) = (αβ)(K;L)
(αK) $\otimes$ (βL) = (αβ)(K $\otimes$ L)
(αK)^* = (α^-)(K^*)

双対を考えるために、Mに対合を要求しました。双対が不要ならMの対合も不要です。

圏の線形化

kを可換体として、Vect_kをk-ベクトル空間の圏とします。Vect_kで豊饒化された圏をk-線形圏（k-linear category）とも呼びます。k-線形関手、k-線形自然変換なども、Vect_k豊饒化の枠組で定義します。

Cを任意の圏として、Cからk-線形圏を作ることができます。次のようにします。

CのホムセットC(A, B)ごとに、自由k-ベクトル空間Lin_k(C(A, B))を作る。ここで、Lin_k(-)は自由k-ベクトル空間を作る操作。
圏の結合 C(A, B)×C(B, C)→C(A, C) をk-線形に拡張して、Lin_k(C(A, B)) $\otimes$ Lin_k(C(B, C))→Lin_k(C(A, C)) を作る。
すると、ホムベクトル空間をLin_k(C(A, B))とするようなk-線形圏ができる。

テンソル積空間を使わなくても、結合を Lin_k(C(A, B))×Lin_k(C(B, C))→Lin_k(C(A, C)) という双線形写像だと定義しても同じことです。

このようにして作ったk-線形圏をLin_k(C)と書くことにします。ホムベクトル空間に関して：

(Lin_k(C))(A, B) = Lin_k(C(A, B))

ホムセットがホムベクトル空間に変わっただけで、対象はもとの圏の対象をそのまま使っていることに注意してください。Lin_k(C)の対象がベクトル空間だとは（一般には）言えません。

Dがk-線形圏のとき、ホムベクトル空間のk-線形構造を忘れてしまえばただの圏となります。この忘却関手をUとすると、U:k-LinCat→Cat となります。ここで、k-LinCatはk-線形圏の圏、Catは圏の圏です。安全のために、小さい圏の範囲で考えています。が、大きな圏でもたぶん大丈夫でしょう。

k-線形化する関手 Lin_k:Cat→k-LinCat と、k-線形構造を忘れる関手 U:k-LinCat→Cat は随伴ペアになっています。

k-LinCat(Lin_k(C), D) $\stackrel{\sim}{=}$ Cat(C, U(D))

$\stackrel{\sim}{=}$ の左右を関手圏と考えて、 $\stackrel{\sim}{=}$ を圏同値と解釈しても随伴関係は成立します。

イデアルによる商線形圏

Dをk-線形圏として、J⊆Mor(D) とします。ここで、Mor(D)は、Dの射全体の集合です。J∩D(A, B) をJ(A, B)と書きます。定義から、J(A, B)⊆D(A, B)。

Jがイデアルであるとは次を満たすことです*3。

J(A, B)はD(A, B)の部分ベクトル空間。
任意の f∈D(X, A) と h∈J(A, B) に対して、f;h∈J(X, B)。
任意の g∈D(B, Y) と h∈J(A, B) に対して、h;g∈J(A, Y)。

J(A, B) = D(A, B) と J(A, B) = {0_A,B} はいずれもイデアルになります。

k-線形圏DとDのイデアルJに関して、新しい圏D/Jを作れます。次のようにします。

|D/J| := |D|
(D/J)(A, B) := D(A, B)/J(A, B) （商ベクトル空間）
結合（composition）と恒等射（identity）はうまいこと定義する。

「うまいこと」を詳しく述べませんが、Jがイデアルであることからうまいこと定義できます。

商線形圏の事例として、セットイド豊饒圏について述べます。集合に同値関係が載った構造をセットイド（setoid、亜集合）と呼び、セットイドを対象として、同値関係を保存する写像を射とする圏をSetoidとします。圏Setoidは、集合の直積をモノイド積として対称モノイド圏だと考えます。

いま、CをSetoid豊饒圏だとします。つまり、C(A, B)はセットイドです。ホムセットイドC(A, B)上の同値関係を〜_A,Bとします。が、たいていの場合、下付きのA,Bは省略します。

D := Lin_k(C) と置きます。CをDに埋め込めば、CはDの広い部分圏*4だとみなせます。f, g∈C(A, B)で、f〜g であるf, gにより f - g と書けるD(A, B)の要素から生成された部分ベクトル空間をJ_~(A, B)とします。そして、J_~(A, B)をすべて寄せ集めた作ったDの射の集合をJ_〜とします。

J_〜はDのイデアルになります。したがって、商線形圏D/J_〜を作れます。一方で、(C/〜)(A, B) := C(A, B)/〜_A,B と定義して圏C/〜を作れます。これらのあいだには、次の圏同値が成立します。

(Lin_k(C))/J_〜 $\stackrel{\sim}{=}$ Lin_k(C/〜)

この同値はk-線形な同値です。ホムベクトル空間ごとに、次のようなベクトル空間の同型を導きます。

Lin_k(C(A, B))/J_〜(A, B) $\stackrel{\sim}{=}$ Lin_k(C(A ,B)/〜_A,B) in Vect_k

テンパリー／リーブ圏の構成

圏のk-線形化とイデアルによる商線形圏の準備ができたので、これらを使ってテンパリー／リーブ圏を構成できます。

C_×を0を除いた複素数として、z^- = (1/zの共役) とすれば、(C_×, ・（掛け算）, 1, (-)^-) は対合を持つ可換モノイドとなります（実際には可換群になってます）。δを非零複素数として、Kauf_{(C_×, δ)} を定義できます。δをサークル乗数とするカウフマン圏です。このカウフマン圏は、非零複素数によるスカラー乗法を持ちますが、線形構造を持つわけではありません。

Kauf_δを複素線形化しましょう。Lin_C(Kauf_δ)を作ります。これで、C-線形圏ができました。Lin_C(Kauf_δ) は長たらしいので、LK_δ（linearlized Kauffman）と略記します。δを省略することもあります。

Kauf_δの射である非零複素係数付きカウフマン図は、LK_δのホムベクトル空間の基底になります。ホムベクトル空間の基底とみなした係数付きカウフマン図は、《αK》のようにギュメで囲むことにします。

LKの射、つまりホムベクトル空間のベクトルXは、

X = Σ_i(ξ_i《α_iK_i》)

のような一次結合の形で書けます。ここで、ξ_i, α_iは非零複素数です。番号iは適当な範囲で動かします。

非零複素数αとカウフマン図Kに対して、α《K》 - 《αK》の形のベクトルで生成されるホムベクトル空間の部分ベクトル空間をすべて寄せ集めてJとします。Jはイデアルになります。例えば、α《K》, 《αK》∈LK(A, B)、《βL》∈LK(B, C) とすると：

  (α《K》 - 《αK》);《βL》
= (α《K》);《βL》 - 《αK》;《βL》
= α《βK;L》 - 《α(βK;L)》

なので、J(A, C)に入ります。

このイデアルJでホムベクトル空間達を割り算すれば、商ベクトル空間では、等式 α《K》 = 《αK》が成立します。要するに商ベクトル空間では、カウフマン圏におけるスカラー乗法と、線形化した後のスカラー乗法がシームレスに計算可能だ、ということです。この事実を利用すると、LK/Jの射Xを、サークルを持たないカウフマン図K_iを使って

X = Σ_i(ξ_i《K_i》)

の形に書けます。この形は、図からサークルを除去した標準形（正規形、既約形）となります。

今作ったLK_δ/Jがテンパリー／リーブ圏TL_δです。

TL_δ := LK_δ/J = (Lin_C(Kauf_δ))/J

ブレイド図の圏

「はじめての圏論中間付録B：アミダとブレイド」で定義したブレイド図の圏を考えます。ブレイド図は、真っ直ぐな紐と以下の2つの交差から結合（縦に並べる）とモノイド積（横に並べる）で作られる図です。（2つの交差のどっちを正にするかは好みの問題です。）対象は自然数（横木上の点の数）です。

ブレイド図の圏をBrDiagとして、正負の交差を B₊, B_-:2→2 in BrDiag とします。「はじめての圏論中間付録B：アミダとブレイド」で注意したように、ブレイド図は“みたままの図形”でイソトピー（に相当する同値関係）による同一視はしてません。したがって、結合／モノイド積すると交差が増える一方で、可逆射は恒等射だけです。

通常ブレイドと言うと、B₊;B_- = id₂ などを仮定します。この状況を記述するために、圏BrDiagをSetoid-豊饒圏としましょう。

圏BrDiagのホムセットBrDiag(n, n)ごとに（n ≠ m ならBrDiag(n, m)は空なので考える必要はない）、ライデマイスターII移動とライデマイスターIII移動により生成される同値関係を考えます。この同値関係をアルチン関係式とも呼ぶので、ここではライデマイスター／アルチン同値関係（Reidemeister-Artin equivalence relation）と呼び、記号〜^RA で表すことにします。以下で、 $\otimes$ はモノイド積、Iはid₁のことです。

B₊;B_- 〜^RA B_-;B₊ 〜^RA id₂
(I $\otimes$ B₊);(B₊ $\otimes$ I);(I $\otimes$ B_-) 〜^RA (B_- $\otimes$ I);(I $\otimes$ B₊);(B₊ $\otimes$ I)

二番目のライデマイスターIII移動は次の図で表されます。

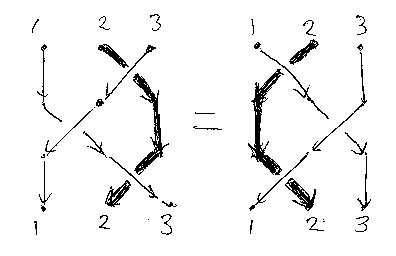
なお、ライデマイスターIII移動の記述にはいくつか変種があります。ここでは、手前の正の交差の奥にある紐を左右に動かしています。

圏BrDiagは、完全に組み合わせ的に定義できますが、BrDiag上の〜^RAは、ブレイドの幾何的な定義におけるイソトピー同値に相当します。例えば、次のイソトピー変形は、組み合わせ的ライデマイスターII移動を2度行う操作に対応します。

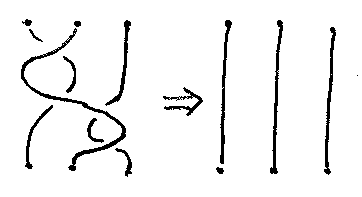
以下では、ブレイド図の圏BrDiagには、同値関係〜^RAを一緒に考えてセットイド豊饒圏とみなします。圏のk-線形化で述べた事実により、次が成立します。

(Lin_k(BrDiag))/J_〜^RA $\stackrel{\sim}{=}$ Lin_k(BrDiag/〜_^RA)
Lin_k(BrDiag(n, n))/J_〜^RA(n, n) $\stackrel{\sim}{=}$ Lin_k(BrDiag(n, n)/〜^RA)

カウフマンのスケイン関係式

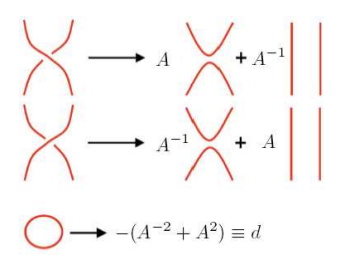
カウフマンのブラケット多項式というもの（ここではその内容に踏み込まない）を定義するとき、次のような不思議な関係式を使うんですよ。

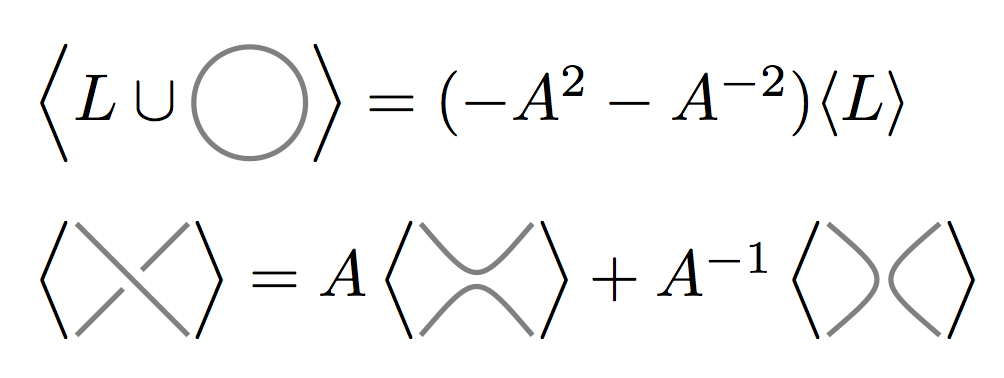
僕は何のことだかサッパリ分かりませんでした。今でも分かってないです。ともかくも、図形にスカラー係数を付けた一次結合のあいだの等式をスケイン関係式（skein relation）と呼ぶので、これは一種のスケイン関係式です。以下、カウフマンのスケイン関係式として参照します。

上記一番目の等式では、サークルを付け加えるとスカラー(-A² - A^-2)が外に出るので、(-A² - A^-2)をサークル乗数とみなせ、ということらしいです。二番目は、ブレイドの生成元がテンパリー／リーブ射（TLの射）と何らかの意味で同値だと言っているようです。

… … ウーム、わからん。

ちょっと解釈を変えて、ブレイド図の圏BrDiagからテンパリー／リーブ圏TLへの関手の定義だとみなしましょう。この解釈なら、（天下りの誹りを免れないが）関手の定義としてハッキリとした意味を与えられそうです。以下でやってみます。

ブレイド図の圏の線形表現

Cを任意の圏として、Vをk-線形圏とします。CからVへの関手をCのk-線形表現（k-linear representation）と呼びます。CとVがモノイド積を持つときは、線形なモノイド関手をk-線形表現とします。以下では、モノイド積は厳密モノイド積だけを考えます。

この言葉遣いが、通常の「線形表現」と矛盾しないことを確認しましょう。Mをモノイド（あるいは群）として、Mの線形表現は、圏とみなしたMからVect_kへの関手となります。k係数行列圏Mat_kへの関手なら行列表現となります。よって、上記の「圏の線形表現」は、モノイド／群の線形表現／行列表現の拡張となっています。

複素係数テンパリー／リーブ圏TL_δは、C-線形モノイド圏です。したがって、ブレイド図の圏BrDiagからTL_δへの線形モノイド関手はC-線形表現です。線形表現 F:BrDiag→TL_δ があれば、それをBrDiagのC-線形化圏にまで拡張した Lin_C(BrDiag)→TL_δ が定義できます。

さて、カウフマンのスケイン関係式を使って線形表現 F:BrDiag→TL_δ を具体的に定義しましょう。次の図が参考になります。

複素定数Aとしては「1の三乗根ω」を使います。ω = (-1 + √(-3))/2 です。-(ω^-2 + ω²) = 1 なので、サークル乗数は1とします。サークルは単に消してしまっていいわけです。

なお、スケイン関係式に登場した定数Aとサークル乗数δのあいだの関係は、

δ = c(A^-n + Aⁿ)

を使うようです。今回のケースでは、c = -1, n = 2 です。Aとδの関係が何に由来するか、僕は知りません。やってみると結果オーライではありますが。

線形表現Fを露骨に書き下すために、もう少し記号の約束をします：キャップ形、カップ形のカウフマン図を∩、∪で表します。∩:0→2, ∪:2→0 in Kauf_δ です。カウフマン圏Kauf_δはテンパリー／リーブ圏TL_δに埋め込めるので、∩:0→2, ∪:2→0 in TL_δ ともみなせます。

H := ∪;∩ : 2→2 in TL_δ と置きます。また、id₂, id₃をI2, I3とも書きます。それと、ω' = (-1 - √(-3))/2 とします。ω'はωの逆数であり共役でもあります。

以上の記号の約束のもとで、C-線形表現 F:BrDiag→TL₁ を次のように定義します。

対象nについては、F(n) := n
F(B₊) := ωH + ω'I2
F(B_-) := ω'H + ωI2

これだけ定義すれば、Fが（厳密な）モノイド関手であることからBrDiag全体に拡張できます。拡張の指導原理となる法則は：

F(id_n) = id_F(n) = id_n
F(n + m) = F(n) + F(m) （対象のモノイド積は足し算）
F(X;Y) = F(X);F(Y)
F(X $\otimes$ Y) = F(X) $\otimes$ F(Y)

ブレイド図の圏BrDiagには、ライデマイスター／アルチン同値関係〜^RAがあります。線形表現関手Fは、ライデマイスター／アルチン同値関係とどう関わるでしょうか？それを次節で探ります。

スケイン関係式とライデマイスター／アルチン同値関係

とりあえず、次の4つの値を計算しましょう。

F(B₊;B_-)
F(B_-;B₊)
F(I $\otimes$ B₊);(B₊ $\otimes$ I);(I $\otimes$ B_-)
F((B_- $\otimes$ I);(I $\otimes$ B₊);(B₊ $\otimes$ I))

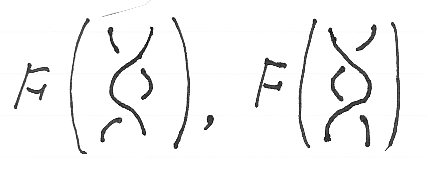
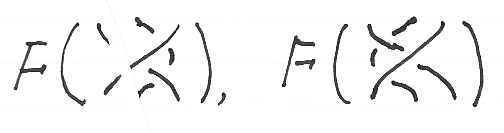
ここから先の計算では、テンパリー／リーブ圏TLでの結合は単に併置でも書くことにします。併置が図式順結合であることに注意してください。

  F(B₊;B_-)
= F(B₊)F(B_-)
= (ωH + ω'I2)(ω'H + ωI2)
= ωω'HH + ωωHI2 + ω'ω'I2H + ω'ωI2I2
= H + ω'H + ωH + I2
= (1 + ω' + ω)H + I2
= I2

途中で、ω, ω'に関する次の等式を使っています。

ωω' = ω'ω = 1
ωω = ω'
ω'ω' = ω
1 + ω' + ω = 0 （ω' + ω = -1）

また、

HH = H;H = H （δ = 1 なので）
HI2 = H;I2 = H
I2H = I2;H = H
I2I2 = I2;I2 = I2

同じように計算すると、F(B_-;B₊) = I2 なので、

F(B₊;B_-) = F(B_-;B₊) = F(id₂)

計算を続けるにあたって、X;Y を [X, Y] と書いていいことにします。カンマは優先順位が低いセミコロン（圏の結合）として使います。id₁ = I, id₂ = I2, id₃ = I3 と書いて、「圏論勉強会：3点テンパリー／リーブ代数の掛け算九九」で導入した次の記号も使います。

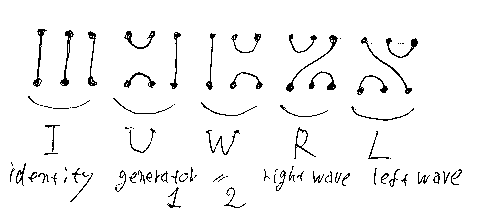
掛け算の表は次のとおり。

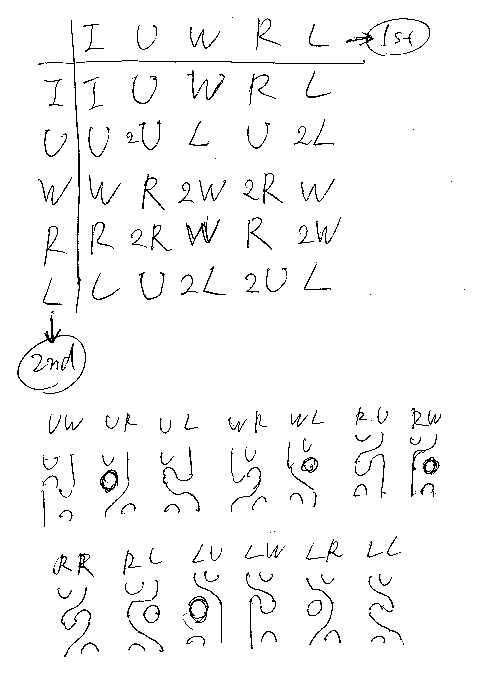
ただし、↑の表は δ = 2 のものですから、δ = 1 に読み替えてください。

では計算します。

  F((IB₊);(B₊I);(IB_-))
= [F(I)F(B₊),
   F(B₊)F(I),
   F(I)F(B_-)]
= [I(ωH + ω'I2),
   (ωH + ω'I2)I,
   I(ω'H + ωI2)]
= [ ωW + ω'I3,
   [ωU + ω'I3,
    ω'W + ωI3]]
= [ ωW + ω'I3,
    UW + ωωUI3 + ω'ω'I3W + I3I3]
= [ ωW + ω'I3,
    R + ωωU + ω'ω'W + I3]
= ωWR + WU + ω'WW + ωWI3 + ω'I3R + ωI3U + I3W + ω'I3I3
= ωW + L + ω'W + ωW + ω'R + ωU + W + ω'I3
= ω'I3 + ωU + (ω + ω' + ω + 1)W + ω'R + L
= ω'I3 + ωU + ωW + ω'R + L

複素数ω, ω'の計算の他に、I $\otimes$ H = W, I $\otimes$ I2 = I3 などのカウフマン図のテンソル積計算もしています。

  F((B_-I);(IB₊);(B₊I))
= [F(B_-)F(I),
   F(I)F(B₊),
   F(B₊)F(I)]
= [(ω'H + ωI2)I,
   I(ωH + ω'I2),
   (ωH + ω'I2)I]
= [[ω'U + ωI3,
    ωW + ω'I3],
    ωU + ω'I3]
= [ UW + ω'ω'UI3 + ωωI3W + I3I3,
    ωU + ω'I3]
= [ R + ω'ω'U + ωωW + I3,
    ωU + ω'I3]
= ωRU + ω'UU + WU + ωI3U + ω'RI3 + UI3 + ωWI3 + ω'I3I3
= ωU + ω'U + L + ωU + ω'U + ω'R + U + ωW + ω'I3
= ω'I3 + (ω + ω' + ω + 1)U + ωW + ω'R + L
= ω'I3 + ωU + ωW + ω'R + L

以上の計算から次が言えます。

F((I $\otimes$ B₊);(B₊ $\otimes$ I);(I $\otimes$ B_-)) = F((B_- $\otimes$ I);(I $\otimes$ B₊);(B₊ $\otimes$ I))

計算結果の解釈

あー疲れた。時間もない。あとは急ぎ足で、何を計算したのかを解釈してみます。細部を確認してないので、大雑把な話です。

線形表現 F:BrDiag→TL_{(C, 1)} をカウフマンのスケイン関係式に基づいて定義すると、「ブレイド図の圏BrDiagをライデマイスター／アルチン同値関係で割った圏BrDiag/〜^RAを、テンパリー／リーブ圏TL₁に埋め込めるよ」というのが今回の話のエッセンスです。

前節の計算から、X 〜^RA Y ならば F(X) = F(Y) が言えます。X 〜^RA Y であるX, Yから作った X - Y という形のベクトル達は、イデアルJ_〜^RAを生成します。F(X - Y) = F(X) - F(Y) = 0 であることから、イデアルJ_〜^RAは、線形表現Fの核（kernel）に入ります。

というわけで J_〜^RA ⊆ Ker(F) は言えてます。逆向きの包含 Ker(F) ⊆ J_〜^RA もたぶん確認できるでしょう。普通の線型代数と同様な準同型定理が成立するなら（大丈夫そう）、(Lin_C(BrDiag))/J_〜^RA $\stackrel{\sim}{=}$ (Lin_C(BrDiag))/Ker(F) $\stackrel{\sim}{=}$ Im(F) が言えます。Im(F)は、k-線形関手Fの像である部分圏を表します。

(Lin_C(BrDiag))/J_〜^RAはLin_C(BrDiag/〜^RA)と同一視可能なので、Lin_C(BrDiag/〜^RA)とIm(F)も同一視できます。これは、ブレイド図達をライデマイスター／アルチン同値関係で割ったモノから張ったベクトル空間達は、テンパリー／リーブ圏のなかにスッポリ入り込むことを意味します。この埋め込みが、カウフマンのスケイン関係式から作られた線形表現Fで実現されるわけです。