僕は、圏の具体例として、テンパリー/リーブ圏TLや平面単純タングルの圏SPTを出すことが多いです。例えば、2008年に書いた「圏論勉強会:3点テンパリー/リーブ代数の掛け算九九」はテンパリー/リーブ圏TLのホムセットTL(3, 3)の話です。2009年のモニャドセミナー「モニャドセミナー2の資料やら補足やらナニヤラ」のホワイトボード写真は、“単純平面タングル=SPTの射”の絵です。
テンパリー/リーブ圏TLや平面単純タングルの圏SPTをよく知っているわけではななくて(僕、よく知らないです)、「圏の対象=集合、圏の射=写像」という誤った思い込みをしないように、紐模様を射とする圏を例に出しています。
TLやSPTの射は模様(絵柄)なので、キャンバスに描きます。キャンバスは2次元の領域です。キャンバスには基準点(マーク)が付いているのですが、この基準点のことを忘れてしまうと混乱します。つうか、僕自身が基準点を忘れて、アレレ?な状況になったので、キャンバスと基準点のことを確認しておきます。
内容:
絵の引用元
次の3つの論文に掲載されている絵を引用します。
- Title: Planar Algebras, I (1999)
- Author: V. F. R. Jones
- Pages: 122p
- URL: https://arxiv.org/abs/math/9909027
- Title: Planar algebras in braided tensor categories (2016)
- Authors: André Henriques, David Penneys, James Tener
- Pages: 91p
- URL: https://arxiv.org/abs/1607.06041
- Title: A Cyclic Approach to the Annular Temperley-Lieb Category (2009)
- Autor: David Penneys
- Pages: 35p
- URL: https://arxiv.org/abs/0912.1320
上から順にJones-1999, Henriques-Penneys-Tener-2016, Penneys-2009と略称します。
平面タングル
平面タングル(planar tangle)の実例を出します。下は、Jones-1999にある絵です。
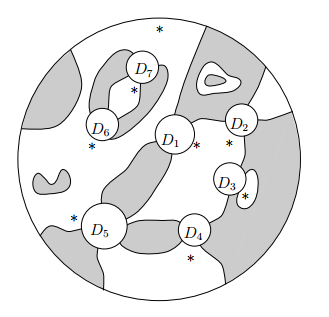
平面内に大きな(つっても大きさはテキトー)な円を描いて、その大きな円板(big disk)から幾つかの小さな円板(little disks)をくり抜きます。穴あきの円板がキャンバスです。上の実例では、小さな円板(穴)がD1からD7の7個あります。外側の大きな円板を入れると全部で8個の円板があります。
それぞれの円板(大小の円板すべて)に星印が1個ずつ付随しています。8個の星印がありますね。これが基準点(マーク)です。絵の描き方としては、星を円周上に乗せたほうが、「円板←→星」の対応関係がハッキリすると思います。
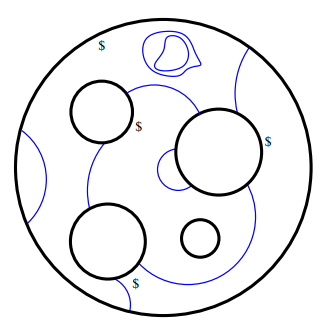
模様(絵柄)は、紐と影(shade)です。今回の話題はキャンバスと基準点なので、模様について詳しくは述べませんが、影のないバージョンがあることを注意しておきます。次の絵は、ジョーンズ(Vaughan F.R. Jones)の講義資料(https://math.berkeley.edu/~vfr/VANDERBILT/pl21.pdf)からの引用ですが、影はありません。基準点は星印じゃなくてドルマークになっています。それと、紐が触ってない穴に基準点(ドルマーク)がないですが、描いておいたほうが整合性が取れるでしょう(使わないので描いてないのですが、描いて悪いことはありません)。
平面タングルの結合
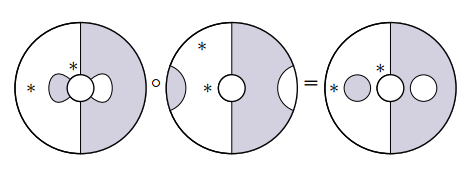
平面タングルの結合(composition)は、通常の圏の結合より少し複雑でオペラッド結合(operadic composition)と呼ばれるやり方をします。絵を見てもらったほうが早いでしょう。再び、Jones-1999にある絵を引用します。
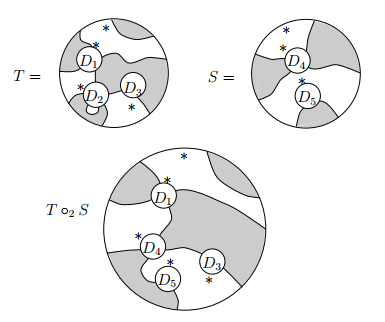
T2S の'
'は反図式順(anti-diagrammatic order)の結合記号です。下付きの2は、Tの2番めの穴D2を使うことを示しています。つまり、Tの2番めの穴にSを縮小してピタッとはめ込むのです。そのとき穴(小さな円板)D2の基準点とS(の大きな円板)の基準点を合わせます。
基準点は、結合の“位置合わせ”のためにあったのです。基準点どうしが重なるだけでなく、模様もズレなくきれいにつながる必要があります。調整のためにトポロジカルな変形*1は自由にしてかまいません。
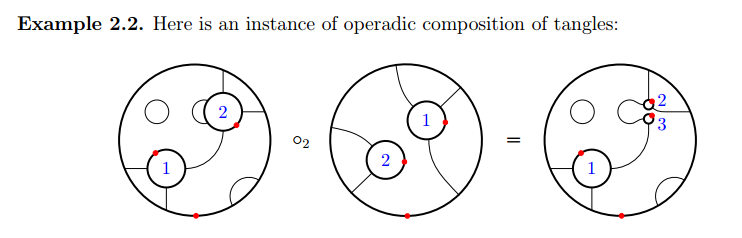
別な絵も見てみましょう。Henriques-Penneys-Tener-2016からの引用です。模様は影なしで、基準点は赤丸で表示してあります。これは分かりやすい絵ですね。結合結果では、穴のリナンバリング「右側1→2, 右側2→3」がされていることに注意してください。
さらにもうひとつ。Penneys-2009からの引用。穴がひとつだけの例です。穴がひとつだけの平面タングルに限れば、普通の圏の結合と同じように結合できます。
矩形タングルと円環タングル
平面タングルは、穴あき円板に描かれた模様です -- キャンバスが穴あき円板なのです。穴がひとつの穴あき円板は円環(annulus)と呼びます。円環をキャンバスとする平面タングルは円環タングル(annular tangle)と呼びます。前節最後の絵は、円環タングルの結合の絵です。
円板ではなくて矩形(rectangle)をキャンバスとする平面タングルは矩形タングル(rectangular tangle)です。矩形タングルの紐は、左右の辺を突き抜けたり左右の辺に触ったりはできません。紐は、上の辺と下の辺に乗っている点を繋ぐだけです。
矩形タングルと円環タングルは次のようにして対応付けできます。(Penneys-2009からの引用)
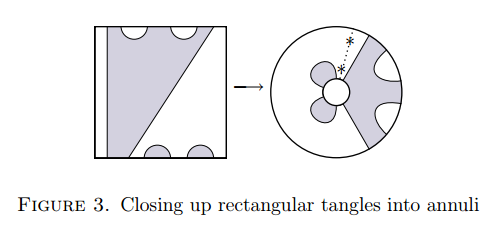
これは、矩形の左右の辺を糊付けしていったん円筒を作り、その円筒をベチャッと潰して、平面内に押し込んだと考えるといいでしょう。上の図では、矩形の上の辺が外側の円に対応しています。また、矩形の左の辺が、円環内の点線で描かれた線に対応しします。
矩形タングルの影無しのバージョンは、テンパリー/リーブ図(Temperley-Lieb diagram)、またはカウフマン図(Kauffman diagram)と呼びます。次の絵はFrederick M. GoodmanとHans Wenzlの短めの解説 http://www.math.ucsd.edu/~hwenzl/miknot.pdf からの引用です -- 影がないテンパリー/リーブ図(カウフマン図)ですね。
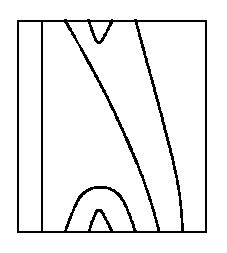
テンパリー/リーブ代数の発見者はテンパリーとリーブですが、図と圏による定式化はカウフマンによるものです。テンパリー/リーブ/カウフマン図という長ったらしい名前を使うと公平でいいかも知れません。
“影なし矩形タングル=テンパリー/リーブ/カウフマン図”を、適当なスカラー係数で線形結合した“ベクトル”達で張られる圏がテンパリー/リーブ圏(Temperley-Lieb category)です。スカラー係数を考えない圏のほうを、僕はカウフマン圏(Kauffman category)と呼んでいます。詳しくは、「テンパリー/リーブ圏とカウフマンのスケイン関係式」を参照してください。テンパリー/リーブ圏とカウフマン圏は大差ないので、神経質に区別しなくてもいいかも知れませんけどね。
円環タングルの影無しのバージョンのほうは、僕は単純平面タングルと呼んでいます。したがって、“影なし円環タングル=単純平面タングル”を射とする圏が単純平面タングルの圏(category of simple planar tangles)となります。
「矩形タングル→円環タングル」という対応の影なしバージョンを考えれば、カウフマン圏(線形構造を持たないテンパリー/リーブ圏)は、単純平面タングルの圏に埋め込むことができます。図のなかに生じるサークル(ループ)を処理するためにモノイド係数を考えることがあります。それについては、「テンパリー/リーブ圏とカウフマンのスケイン関係式」に書いてあります。
単純平面タングルの切り開き
カウフマン圏をKaufとします(テンパリー/リーブ圏TLと大差ないです)。単純平面タングルの圏をSPTとします。前節の議論から、Kauf→SPT という関手があります。モノイド係数を考えるならば、モノイドMとMの要素δを指定して Kauf(M, δ)→SPT(M, δ) ですが、細かいことは気にしないことにします。(気になるなら「テンパリー/リーブ圏とカウフマンのスケイン関係式」参照。)
埋め込み関手 Kauf→SPT は可逆でしょうか? 別な言い方をすると、任意の単純平面タングルに対して、対応するカウフマン図(=影なし矩形タングル)があるでしょうか? この対応において、単純平面タングルの2個の基準点を繋ぐ線(模様の紐ではない)が、カウフマン図の左のキャンバス境界辺に対応しなくてはなりません。これは、円環を基準点を繋ぐ線に沿って切り開いて、トポロジカルな変形をしてカウフマン図(影なし矩形タングル)にできるか? という問題になります。
単純平面タングルの切り開きは一般的には無理です。紐が一本だけのケースでも切り開けない単純平面タングルがあります。
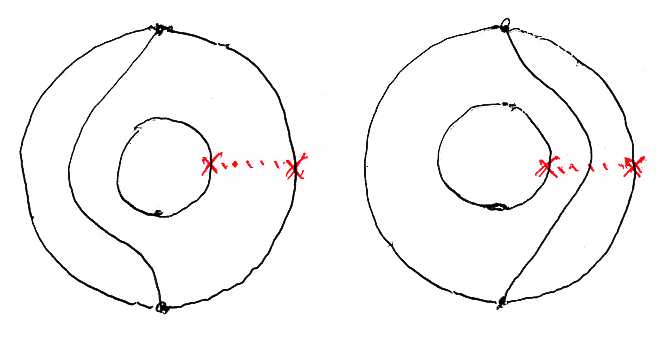
左の単純平面タングルは点線で切り開いてカウフマン図にできますが、右の単純平面タングルは切り開くときに紐も切ってしまうのでカウフマン図にはなりません。これで、SPTはKaufより大きいことが分かりました。実際のところSPTはKaufより格段に複雑です。