回転群の具体的な表示と計算 - 檜山正幸のキマイラ飼育記 (はてなBlog)

今週のはじめ（月曜日）、Mさんに「リー群ってナニ？」と聞かれました。僕もよく知らないので、雰囲気的な絵を描いて「だいたいこんな感じのヤツでしょ、たぶん」みたいなことをゴニョゴニョ言ったんですが、この記事で、回転群に限定して具体的に表示・計算してみます。

3次元回転群の準備として2次元回転群の話を始めたのですが、2次元で息切れしてしまい、3次元の話はオマケ扱いです。あいすみません。

内容：

事例と記法
行列の計算器
2次行列環と2次行列群
2次の直交群O2
2次の特殊直交群SO2
O2の形状とパラメータ表示
SO2の形状とパラメータ表示
3次の直交群O3と特殊直交群SO3
SO3のパラメータ表示

続き：回転群の指数写像の具体的な表示と計算

指数関数・三角関数の級数表示
行列の指数関数
2次歪対称行列の指数関数
指数写像の解釈
SO(n)の単位元における接空間
指数法則
指数写像の微分
1パラメータ指数写像
Alt(3)の基底と回転の力学

事例と記法

2つの具体例を扱います（定義は後で述べます）。

SO(2) 2次元の特殊直交群
SO(3) 3次元の特殊直交群

基礎となるスカラー体（実数体R）までチャンと書けば、SO(2, R), SO(3, R) （あるいは、SO(R²), SO(R³)）ですが、面倒なんでスカラー体Rは省略します。さらに、括弧も鬱陶しいので、SO2, SO3と記すことにします。特殊直交群を回転群とも呼ぶので、SO2は2次元回転群, SO3は3次元回転群です。

抽象的なセッティングではなくて、すべて具体的な行列として扱います。行列の全体は、必要に応じてユークリッド空間と同一視します。つまり、

(2×2行列の全体) $\stackrel{\sim}{=}$ R^2×2 = R⁴
(3×3行列の全体) $\stackrel{\sim}{=}$ R^3×3 = R⁹

すべての議論を、適当なnに対するユークリッド空間Rⁿのなかで行うので、多様体やファイバー・バンドルの知識は不要です。

行列（正方行列しか扱わない）の成分は、二重インデックスではなくて、単一のインデックス（連番）で識別します。

$\begin{pmatrix}{\it x_1} & {\it x_3} \\ {\it x_2} & {\it x_4} \\ \end{pmatrix}$
$\begin{pmatrix}{\it x_1} & {\it x_4} & {\it x_7} \\ {\it x_2} & {\it x_5} & {\it x_8} \\ {\it x_3} & {\it x_6} & {\it x_9} \\ \end{pmatrix}$

こういう書き方をするのは、行列をタプル（列ベクトル／行ベクトル）として扱いたいことが多いからです。2×2行列は X = (x₁, x₂, x₃, x₄) というタプル、3×3行列なら X = (x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉) というタプルと見なすことが多々あります。

2×2行列を2次行列、3×3行列を3次行列とも呼びます。「2次」「3次」と言っても、多項式の次数とは何の関係もないので注意してください。ここでの次数は単に行列のサイズ、または行列が線形変換として作用する空間の次元のことです。

2次行列の空間R⁴と3次行列の空間R⁹には、標準的な内積から距離／位相が入ります。標準的な内積とは：

(X|Y) = x₁y₁ + x₂y₂ + x₃y₃ + x₄y₄
(X|Y) = x₁y₁ + x₂y₂ + x₃y₃ + x₄y₄ + x₅y₅ + x₆y₆ + x₇y₇ + x₈y₈ + x₉y₉

これらの内積は、行列の転置(-)^tと掛け算 $\circ$ とトレースtrを使って、次のように書けます。

(X|Y) = tr(X^t $\circ$ Y)

行列の計算器

僕は計算が出来ないし、仮に出来てもやるのが面倒なんで、高級電卓（Maximaともいう）を使います。例えば、前節最後の内積の定義を確認するには次のようにします*1。

X : transpose(matrix([x_1, x_2, x_3], [x_4, x_5, x_6], [x_7, x_8, x_9]));
Y : transpose(matrix([y_1, y_2, y_3], [y_4, y_5, y_6], [y_7, y_8, y_9]));
transpose(X);
transpose(X) . Y;
mattrace(transpose(X) . Y);

応答も含めた画面ショットは：

なぜかMaximaでは、番号順のソートが逆順なんですが、気にしないことにします。本文中の番号（下付き添字）の順序が逆順なときは、Maximaからのコピペをそのまま使っているからです。気にしないでください。

Maximaの紹介が目的ではないので、以下、Maximaに関する説明はしません。僕は計算に使いますけどね。あしからず。

2次行列環と2次行列群

サイズ2×2の正方行列の全体を、ここではM2と書きます。M2は、ベクトル空間としては R^2×2 = R⁴ と同じものです。M2と書くときは、行列の掛け算を一緒に考えた非可換環を意図していて、この意味のM2は2次行列環（ring of 2-by-2 matrices）と呼びます。M2のゼロをO₂, 単位（イチ）をE₂と書くことにします。混乱の恐れがなければ、下付きの2は省略してO, Eも許容します。

$\mathrm{O} = \mathrm{O}_2 = \begin{pmatrix} 0 & 0 \\ 0 & 0\end{pmatrix} \\ \mathrm{E} = \mathrm{E}_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}$

M2の掛け算に関する可逆元の全体をM2_×とします。

M2_× = {X∈M2 | det(X) ≠ 0}

ここで、detは行列式（determinant）で、X = (x₁, x₂, x₃, x₄) とM2の元を長さ4のタプルで表すなら：

det(X) = det(x₁, x₂, x₃, x₄) = x₁x₄ - x₂x₃

detは4変数の多項式なので、det(X) = 0 はR⁴内の次元3の図形を定義し、M2_×はこの図形の補集合になります。

M2_× = M2＼{X∈M2 | det(X) = 0} （'＼'は集合差）

行列の掛け算に関して群とみなしたM2_×を、2次行列群（group of 2-by-2 matrices）または2次の一般線形群（general linear group of degree 2）と呼びます。2次の一般線形群は、しばしばGL(2, R)と書かれます。この記事の略記法に従えば、GL(2, R) = GL(2) = GL2 です。

M2_× = GL(2, R) = GL(2) = GL2

2次の直交群O2

さて、2次元の回転群SO2を定義したいのですが、その前に O2 = O(2) = O(2, R) を定義します。O2は2次の直交群（orthogonal group of degree 2）と呼ばれる群ですが、とりあえずはO2を、M2（ベクトル空間／アフィン空間としてはR⁴）内の図形として定義します。O2は次の方程式で定義される図形です。

X^t $\circ$ X = E₂

ここで、 $\circ$ は行列の掛け算、(-)^tは行列の転置です。2×2行列XをR²の線形変換とみなした場合、上の方程式は「XはR²の標準内積を保存する」と読めます。内積の保存は、幾何的には長さと角度を変えないことです。

上記方程式を成分で露骨（explicit）に書けば：

$\begin{pmatrix}{\it x_2}^2+{\it x_1}^2 & {\it x_2}\, {\it x_4}+{\it x_1}\,{\it x_3} \\ {\it x_2}\,{\it x_4}+ {\it x_1}\,{\it x_3} & {\it x_4}^2+{\it x_3}^2 \\ \end{pmatrix}=\begin{pmatrix}1 & 0 \\ 0 & 1 \\ \end{pmatrix}$

成分ごとにばらしてみると：

${\it x_2}^2+{\it x_1}^2 = 1$
${\it x_2}\, {\it x_4}+{\it x_1}\,{\it x_3} = 0$
${\it x_2}\,{\it x_4}+ {\it x_1}\,{\it x_3} = 0$
${\it x_4}^2+{\it x_3}^2 = 1$

2番目と3番目は同じ方程式なので、4変数3連立方程式系になります。この方程式系で定義される図形は、次元が3落ちて1次元の図形だろうと推測できます。（上記方程式系の解集合である図形の詮索はまた後でします。）

O2が群になるとは次のことです。

X, Y∈O2 ならば、X $\circ$ Y∈O2
E₂∈O2
X∈O2 ならば、X^-1∈O2

成分を使って露骨に計算してもいいですが、「X∈O2 ⇔ X^t $\circ$ X = E₂」だけを使っても簡単に出ます。成分を使わない方法を使えば、2次（2×2）に限らず、任意のnに対するO(n)が群であることを示せます。

2次の特殊直交群SO2

X∈O2 だとすると、det(X) = ±1 です。なぜなら； X∈O2 ⇔ X^t $\circ$ X = E₂、等式の両辺の行列式を取って、det(X^t $\circ$ X) = det(E₂) = 1。det(X $\circ$ Y) = det(X)det(Y)、det(X^t) = det(X) なので、det(X)² = 1、したがって、det(X) = ±1。

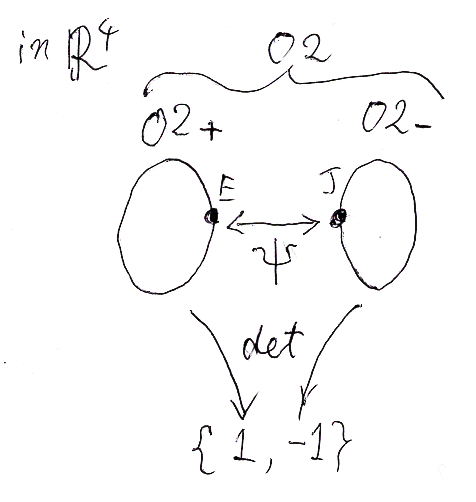
このことから、O2は、det(X) = 1 の部分と、det(X) = -1 の部分に分割されることが分かります。det(X) = 1 であるほうをO2₊、det(X) = -1 であるほうをO2_-とします。

O2₊ = {X∈O2 | det(X) = 1}
O2_- = {X∈O2 | det(X) = -1}
O2 = O2₊∪O2_- （O2₊∩O2_- = $\emptyset$ ）

detをO2に制限した det:O2→{1, -1} が群の準同型写像であることから、O2₊ = det^-1(1) はO2の部分群になります。群構造を考えたO2₊をSO2と書いて、2次の特殊直交群（special orthogonal group of degree 2）と呼びます。冒頭で述べたように、特殊直交群の別名が回転群なので、SO2は2次元の回転群（2-d rotation group）です。SO2の元をR²の線形変換とみなせば、長さと角度、さらに向き（orientation）を変えない変換です。

群の全射準同型写像 det:O2→{1, -1} に群の準同型定理を適用すると、O2/SO2 $\stackrel{\sim}{=}$ {1, -1} となるはずです。商集合O2/SO2は、{O2₊, O2_-}ですが、同値類の代表元を使ったほうが分かりやすいでしょう。E, Jは次の行列とします。

$\mathrm{E} = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix} \in \mathrm{O2}_{+} \\ \mathrm{J} = \begin{pmatrix} 1 & 0 \\ 0 & -1\end{pmatrix} \in \mathrm{O2}_{-}$

E, Jの群表（群の二項演算表）を書くと：

	E	J
E	E	J
J	J	E

確かに、{1, -1}と同型になっています。

任意の2次行列Xに行列Jを右から掛ける操作をΨとします。

Ψ(X) := X $\circ$ J

X = (x₁, x₂, x₃, x₄) とタプル形式に書いて、Ψを成分表示すると：

Ψ(X) = Ψ(x₁, x₂, x₃, x₄) = (x₁, x₂, -x₃, -x₄)

ΨをR⁴に働く変換とみなすと、2本のベクトル(1, 0, 0, 0)と(0, 1, 0, 0)で張られる平面（2次元部分ベクトル空間）を対称面とする対称（鏡映）変換となっています。ΨはO2₊をO2_-に移し、O2_-をO2₊に移します。特に：

Ψ(E) = J
Ψ(J) = E

O2₊とO2_-は、Ψの対称面（不動点集合）に対して鏡映の関係にあります。当然に、O2₊ = SO2 とO2_-は図形として合同です。

O2の形状とパラメータ表示

O2 = O2₊∪O2_- の、R⁴内の図形としての位置・形状をハッキリさせましょう。

もう一度O2の定義方程式を確認します。

${\it x_2}^2+{\it x_1}^2 = 1$
${\it x_2}\, {\it x_4}+{\it x_1}\,{\it x_3} = 0$
${\it x_4}^2+{\it x_3}^2 = 1$

1番目と3番目はどちらも円周の方程式ですが、1番目はx₁-x₂平面内の円周、3番目はx₃-x₄平面内の円周です。よって、1番目と3番目の方程式の連立方程式系の解集合はR⁴内のトーラスになります（以下の箇条書きと、下にある図を参照）。

R²_1,2 = {(x₁, x₂) | x₁, x₂∈R }
R²_3,4 = {(x₃, x₄) | x₃, x₄∈R }
S¹_1,2 = {(x₁, x₂)∈R²_1,2 | x₁² + x₂² = 1}
S¹_3,4 = {(x₃, x₄)∈R²_3,4 | x₃² + x₄² = 1}
{(x₁, x₂, x₃, x₄)∈R⁴ | x₁² + x₂² = 1} = S¹_1,2×R²_3,4
{(x₁, x₂, x₃, x₄)∈R⁴ | x₃² + x₄² = 1} = R²_1,2×S¹_3,4
{(x₁, x₂, x₃, x₄)∈R⁴ | x₁² + x₂² = 1 かつ x₃² + x₄² = 1} = (S¹_1,2×R²_3,4)∩(R²_1,2×S¹_3,4)
(S¹_1,2×R²_3,4)∩(R²_1,2×S¹_3,4) = S¹_1,2×S¹_3,4 = (R⁴内のトーラス)

円周S¹_1,2をパラメータαでパラメータ表示し、円周S¹_3,4をパラメータβでパラメータ表示すると、トーラスの2パラメータ表示が得られます。

x₁ = cos(α)
x₂ = sin(α)
x₃ = cos(β)
x₄ = sin(β)

あるいは、

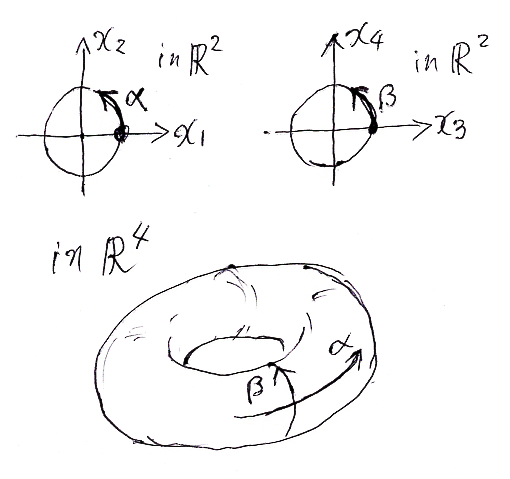
$\begin{pmatrix}{\it x_1} & {\it x_3} \\ {\it x_2} & {\it x_4} \\ \end{pmatrix} = \begin{pmatrix}cos(\alpha) & cos(\beta) \\ sin(\alpha) & sin(\beta) \end{pmatrix}$

ドーナツ型の星があるとして、αを経度、βを緯度と呼びましょう。α, βは任意の実数でいいとしますが、周期2πでラップアラウンドします。例えば、経度0・緯度0と経度-4π・緯度2πは同じ地点です。

ドーナツ星が地球と違うのは、北極・南極のような経緯度の特異点がなくて、メルカトル図法が星全体の正確な地図として使えることです。ドーナツ星は、平面R²に無限回繰り返し展開されます。M:R²→S¹_1,2×S¹_3,4 を、無限回繰り返しメルカトル地図からドーナツ表面（トーラス）への写像（文字通り“マップ”）とします。

M(α, β) := (cos(α), sin(α), cos(β), sin(β))

目的の図形O2は、このドーナツ表面（トーラス）の部分集合になっているので、メルカトル地図上では平面内の繰り返し（周期的）図形として現れるはずです。

O2を定義する残りの方程式は：

${\it x_2}\, {\it x_4}+{\it x_1}\,{\it x_3} = 0$

αとβで書くと：

sin(α)sin(β) + cos(α)cos(β) = 0

三角関数の加法定理から：

cos(α - β) = 0

三角関数の周期性から：

α - β = nπ + (1/2)π （n∈Z）

これを、メルカトル地図、つまりα-β平面内に描くと、平行に走る斜め直線の集まりになります。0≦α≦2π, 0≦β≦2π の正方形を地図の基本領域として、基本領域内を横切る直線だけを選ぶと：

β = α - 3π/2
β = α - π/2
β = α + π/2
β = α + 3π/2

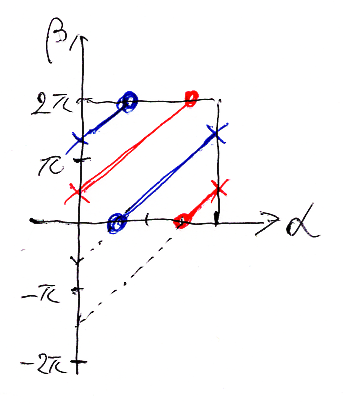
ドーナツ表面（トーラス）上では、これらの直線がラップアラウンドされるので、輪（円周S¹と同相な図形）になります。4本の直線が2本ずつ組になって、ドーナツ面（トーラス）に巻き付く2つの輪ができます。

結局、O2はR⁴内に埋め込まれた“2つの円周”の形をしていることになります。2つの円周を表現するR²上の直線として、次の2つを選びます。

β = α + π/2
β = α + 3π/2

それぞれの円周をパラメータαで表示すると：

R₊(α) = M(α, α + π/2) = (cos(α), sin(α), cos(α + π/2), sin(α + π/2)) = (cos(α), sin(α), -sin(α), cos(α))
R_-(α) = M(α, α + 3π/2) = (cos(α), sin(α), sin(α + 3π/2), cos(α + 3π/2)) = (cos(α), sin(α), sin(α), -cos(α))

あるいは：

$\mathrm{R}_{+}(\alpha) = \begin{pmatrix}cos(\alpha) & -sin(\alpha) \\ sin(\alpha) & cos(\alpha) \end{pmatrix}$
$\mathrm{R}_{-}(\alpha) = \begin{pmatrix}cos(\alpha) & sin(\alpha) \\ sin(\alpha) & -cos(\alpha) \end{pmatrix}$

R₊:R→R⁴がO2₊をパラメータ表示し、R_-:R→R⁴がO2_-をパラメータ表示します。O2₊とO2_-は Ψ(X) = X $\circ$ J により鏡映の関係だったので、次の等式が成立します。

R_-(α) = Ψ(R₊(α)) = R₊(α) $\circ$ J

具体的には：

$\begin{pmatrix}cos(\alpha) & sin(\alpha) \\ sin(\alpha) & -cos(\alpha) \end{pmatrix} = \begin{pmatrix}cos(\alpha) & -sin(\alpha) \\ sin(\alpha) & cos(\alpha) \end{pmatrix}\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}$

全般的な状況は、次のような感じです。

SO2の形状とパラメータ表示

前節で述べたように、O2₊は R₊:R→R⁴ でパラメータ表示されます。R₊を単にRと書くことにします。また、群としてのO2₊をSO2と書くので：

R:R→SO2 （SO2⊆R⁴）

R(α)は実際、平面R²における回転角αだけの回転を表す行列です。α |→ R(α) は、Rを足し算の群とみると準同型写像になっています。

R(α + α') = R(α') $\circ$ R(α)
R(1) = E₂
R(-α) = R(α)^-1

群の準同型定理から：

SO2 $\stackrel{\sim}{=}$ R/2πZ

図形としてのSO2は円周の形で、写像Rは、直線Rを円周にグルグル巻きつける写像になっています。このグルグル巻きは、螺旋階段を連想させます。

このテの螺旋っぽい話は過去記事に書いたことがあります。

3次の直交群O3と特殊直交群SO3

O2の2を3に変えるだけの定義を、以下にズラズラと列挙します。実際には、3だけじゃなくて一般のnに対しても成立することです。

3×3の行列全体に線形構造と掛け算を考えた非可換環を3次行列環と呼び、 M3と書く。M3のゼロをO₃、単位をE₃で表す。
M3の可逆な元の集合{X∈M3 | det(X) ≠ 0}をM3_×とする。掛け算に関する群としてのM3_×を3次行列群または3次の一般線形群と呼び、M3_× = GL(3, R) = GL(3) = GL3 と書く。
{X∈M3 | X^t $\circ$ X = E₃}は、M3_×の部分群となる。これを3次の直交群と呼び、O(3, R) = O(3) = O3 と書く。
{X∈O3 | det(X) = 1}は、O3の部分群となる。これを3次の特殊直交群または3次元回転群と呼び、SO(3, R) = SO(3) = SO3 と書く。

群の準同型写像 det:O3→{1, -1} を考えることにより、O3/SO3 $\stackrel{\sim}{=}$ {1, -1} であることも2次のときと同様で、O3は O3₊∪O3_- （O3₊∩O3_- = $\emptyset$ 、O3₊ = SO3）と分割され、O3₊とO3_-が互いに鏡像になることも分かります。

鏡像を作るには、2次のJ（= J₂）と類似した3次行列J₃を使います。

$\mathrm{J}_3 = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{pmatrix}$

SO3のパラメータ表示

SO2に関しては、その定義方程式 X^t $\circ$ X = E₂ から出発して、R⁴のなかでのSO2の位置と形状を探ってパラメータ表示を求めました。SO3の場合、外の空間は9次元のR⁹だし、O3, SO3の形状も複雑です。もう疲れたので、ここでは、よく知られたパラメータ表示を紹介するだけにします。

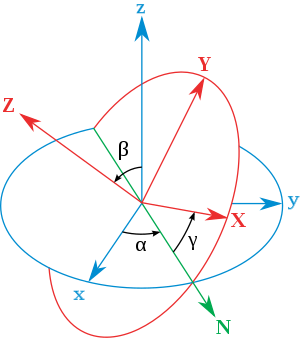
x軸（第一軸）、y軸（第ニ軸）、z軸（第三軸）を回転軸とする3次元回転の行列をそれぞれ、RX, RY, RX とします。

$\mathrm{RX}(\alpha) = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \\ \end{pmatrix}$
$\mathrm{RY}(\beta) = \begin{pmatrix}\cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \\ \end{pmatrix}$
$\mathrm{RZ}(\gamma) = \begin{pmatrix}\cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

3次元空間内での一般的回転を記述するために次の手順がよく使われます（オイラー角、下の絵を参照）。

z軸を回転軸として、αだけ回転する。
回転後のx軸（下図では緑）を回転軸として、βだけ回転する。
回転後のz軸（下図では赤のZ）を回転軸として、γだけ回転する。

この手順は、行列の掛け算として RZ(γ) $\circ$ RX(β) $\circ$ RZ(α) と書けます。行列の掛け算は、時間順としては右から左に並んでいることに注意してください。実際に計算して（Maximaに計算させて）みると：

$\begin{pmatrix}\cos \gamma\,\cos \alpha-\sin \gamma\,\sin \alpha\, \cos \beta & -\sin \gamma\,\cos \alpha\,\cos \beta-\cos \gamma\, \sin \alpha & \sin \gamma\,\sin \beta \\ \cos \gamma\,\sin \alpha\, \cos \beta+\sin \gamma\,\cos \alpha & \cos \gamma\,\cos \alpha\, \cos \beta-\sin \gamma\,\sin \alpha & -\cos \gamma\,\sin \beta \\ \sin \alpha\,\sin \beta & \cos \alpha\,\sin \beta & \cos \beta \\ \end{pmatrix}$