次の論文は、2012年に書かれたフォング〈Brendan Fong〉の修士論文です*1。
- Title: Causal Theories: A Categorical Perspective on Bayesian Networks
- Author: Brendan Fong
- Pages: 77p
- URL: https://arxiv.org/abs/1301.6201 *2
タイトルが「因果の理論」だし、ベイジアンという形容詞も出てくるので、統計的因果推論の話だと思うでしょうが、そうじゃないです。フォングの志としては、統計的因果推論方面への応用を目指しているのかも知れませんが、この論文の内容がそっち方面だと思うと理解に苦しむことになります。
その他にも、誤解を生みそうな表現(悪意のないレッドヘリング)が含まれているので、この記事で注意をしておきます。たまたま最近、マルコフ圏を知ったので、マルコフ圏からの観点を織り交ぜます。
内容:
続きの記事:
セオリーと因果
フォング論文は次の5章から構成されます。
- モノイド圏に関する準備〈Preliminaries on Monoidal Categories〉
- 圏論的確率論〈Categorical Probability Theory〉
- ベイズ・ネットワーク〈Bayesian Networks〉
- 因果セオリー〈Causal Theories〉
- 確率因果モデルの構造〈The Structure of Stochastic Causal Models〉
1章、2章で、圏論的確率論をザッと説明しています。2020年の今ならマルコフ圏ベースの定式化で語りたい内容です。3章は、章タイトルであるベイズ・ネットワークの話もしてますが、ごく簡略で、どっちかというと条件付き確率と独立性の説明です。
4章と5章がフォングのオリジナルな部分です。4章のタイトルを「因果セオリー」とカタカナの「セオリー」にしたのは理由があります。地の文で使う国語辞書的意味の「理論」とはまったく違う意味だからです(Theoriesと複数形なことにも注意)。
“セオリー〈theory〉”の普通ではない使い方は、ローヴェア〈William Lawvere〉に由来します。ローヴェアは鋭い洞察力と豊富なアイディアを持った圏論の大家ですが、人を悩ます奇妙なネーミングをします。その例を挙げれば:
ローヴェアの代数理論(現在は"Lawvere theory"と呼ばれることが多い)は、代数学の理論という意味ではありません。とある条件を満たす圏のことを代数理論と呼ぶのです。僕は、少しでも混乱を避けるために代数セオリー(またはローヴェア・セオリー)とカタカナの「セオリー」を使います。
フォングの因果セオリーも、とある条件を満たす圏のことです。そのような圏はたくさんあるので、通常は複数形 theories を使います。群に関する理論を群論〈theory of groups | group theory〉と呼ぶのと同じ言葉づかいをするなら、フォングが研究した分野は因果セオリー論〈theory of causal theories | causal theory theory〉です。
「因果」という言葉も、必ずしも「原因があって結果が起きる」ことを意味してません。AとBのあいだに何らかの関係性があるとき、それに向きをつけたもの(例えば、B→A の向き)を因果関係〈causal relationship〉と呼んでいるだけです。フォングの意味の因果関係が、現実世界の因果関係をモデル化している保証はありません。国語辞書的な「因果」の意味は忘れて、単なるテクニカルタームとして扱いましょう。
フォングは、強い印象を喚起する言葉をテクニカルタームに採用するのが好きみたいです*3が、国語辞書的意味が強すぎると言霊問題を引き起こします。テクニカルタームの定義は書いてあるので、ドライに(連想を働かせずに)形式的定義だけで了解しましょう。
因果セオリーと呼ばれる圏
我々は、圏とその上の付加構造を分類して、デカルト圏、モノイド圏、コンパクト閉圏のような名前を付けています。因果セオリーも、圏のタイプに付けた名前です。マルコフ圏の概念を使えば、因果セオリーは簡潔に記述できます(後述)。
まず、因果構造を定義しておきます。因果構造〈causal structure〉とは、サイクルを持たない有向グラフで、次の条件を満たすものです。
- 2つの頂点を結ぶ有向辺は高々1本である。
有向グラフの頂点を確率変数〈random variable〉(あるいは単に変数〈variable〉)と呼びます。確率変数とは頂点のことです。それ以上の意味を勝手に想定しないでください。あなたが既に知っている確率変数のことは、ここでは忘れてください。有向グラフの頂点が確率変数です。
有向グラフの辺を因果関係〈causal relationships〉と呼びます。繰り返します; 有向グラフの辺が因果関係です。テクニカルタームとして、今はそう呼ぶ、それだけ。
フォングの定義では、圏の種別としての因果セオリーと、圏を作り出す手段としての因果セオリーがイマイチ不明瞭なので、ここではそれらを区別しましょう。圏の種別としての因果セオリーは、小さな厳密対称厳密マルコフ圏〈small strictly-symmetric strict Markov category〉です*4。と言っても、あまりにもケンロン・ケンロンしていて意味不明でしょうが、ともかくも圏論内部で定義できる圏論的概念なのです。この時点では、確率や統計とは(形式上は)何の関係もありません。
因果構造(有向グラフのことでした)があると、因果構造から因果セオリー(圏のことでした)を作ることができます。因果構造Gを含む最小の因果セオリーを としましょう*5。
という対応は、因果構造の圏から因果セオリーの圏への関手になります*6。フォングは、関手
のことも因果セオリーと呼んでますが、これは因果セオリー生成関手〈causal theory generating functor〉とか呼んだほうがいいでしょう。
因果モデルと呼ばれる関手
Gを因果構造とすると、 は因果セオリーになります。因果セオリーの理論が扱う対象物である因果セオリーは、生成系として因果構造を持つような因果セオリーです(それが理由で、因果セオリー生成関手と因果セオリーをあまり区別しないのでしょう)。
Dがマルコフ圏であるとき、因果セオリー からDへのマルコフ圏構造を保つタイト・モノイド関手(いわばマルコフ関手)を因果モデル〈causal model〉と呼びます(モノイド関手については「図式思考の例として、ラックス・モノイド関手について考えてみる」参照)。こういう定式化も、ローヴェアの代数セオリーの理論を踏襲しています。ローヴェア流なんです。スピヴァックのデータベース理論もローヴェア流です。結果的に、スピヴァックとフォングの理論構成はとても似ています。そして、スピヴァックとフォングは、MITのオンラインコース"Applied Category Theory"を一緒に担当しています。
集合圏Setはマルコフ圏なので、因果モデル を考えることができます。因果モデルにより、確率変数(有向グラフの頂点)に集合が割り当てられ、因果関係(有向グラフの辺)の束に写像が割り当てられます。
因果セオリーや因果モデルの目的からすると、集合圏をターゲット圏にしてもあまり面白くありません。確率的な現象を記述するための圏である“ジリィモナドのクライスリ圏”をターゲット圏にするときが本領発揮です。フォングが採用している確率的なターゲット圏はCGStoc(とそれから派生した圏)です。CGStocは扱いやすい可測空間(countably generated measurable space)を対象とした“ジリィモナドのクライスリ圏”です。奇しくも、ジリィモナドの発案者もローヴェアです(「分布から拡散へ: ミシェル・ジリィを巡って」参照)。
ストリング図の描き方
最後に、フォングのストリング図の描き方で気になったところがあるので注意しておきます。例えば、次の左はフォングのストリング図です。下から上の向きで読みます(「双対や随伴に強くなるためのトレーニング」参照)。右は僕が手描きした絵で、同じ内容を表します。
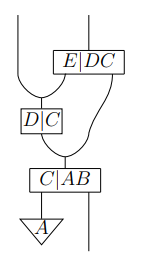
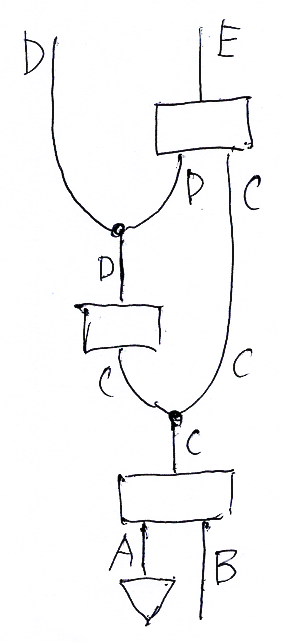
フォングの絵は、ワイヤーに関する情報(対象の名前)をノードに書き込んでいます。例えば、下にある四角形は AB→C という射を表しますが、射のプロファイル(域と余域)を C|AB というテキストにして押し込めています。その代わりワイヤーにはラベルを付けません。
[追記]フォングがこのような描画法を使うには理由があります。なので、視認性だけで一概に判断するのはよくないですね。このことについては:
[/追記]
テキスト記法に合わせるために、このような方式で描いているのですが、視認性が悪く、おすすめできませんね。絵は普通に描いて、絵とテキストの翻訳規則を明示すればいいのではないかと思います。
おわりに
フォングの論文は、用語法・記法・描画法が変わっていて、読みやすいとは言えません。曰く有りげな言葉を使っていますが、やっていることは圏論的な議論なので、言霊に惑わされないでドライに読めば、内容に変なところはありません。
フォングの言葉づかいをそのまま使うことは、混乱と誤解のリスクが高すぎて出来ないでしょうし、今ならマルコフ圏を使って整理したい感じもします。が、ベイズ・ネットワーク〈グラフィカル・モデル〉に、シッカリとした圏論的意味論を与えた点は評価できます。
*1:この記事を書いた理由は、この論文を読む人がいそうなので、読むときの注意を述べるためです。
*2:http://www.cs.ox.ac.uk/bob.coecke/Brendan_Fong.pdf も同じです。
*3:[追記]この憶測は間違いだと思います。「フォングは何故「確率変数」と呼んだのか」参照。[/追記]
*4:厳密対称性の仮定は要らない、むしろ邪魔な気がします。
*5:フォングの論文では、 ではなくて
*6:僕は、グラフのような図形から圏を生成するオペレータを、右肩ダイヤモンドで表します。 です。