アレンジメント計算 2：簡単な実例と注意事項 - 檜山正幸のキマイラ飼育記 (はてなBlog)

次回は、Arrgmnt(P) の代数構造について述べる予定です。

この予定は変更します。説明のための事例が欲しいので、簡単な事例を挙げます。事例を理解するには、圏論的確率論の予備知識は要りません。この記事の事例は今後も参照するかも知れません。事例の状況設定はかなり簡素化しているので、最後にその点を注意します。それと、落とし穴や混乱の原因になりそうなことも折々注意します。

この記事での図の描画方向は「アレンジメント計算 1：確率グラフィカルモデル // アレンジメントとアレンジメント図」で述べたように上から下です。

内容：

因子グラフ、ストリング図へのラベリング
アレンジメント、その直感的な導入
マルコフ行列
マルコフテンソル
マルコフテンソルのプロファイル
アレンジメントの組み立て方
今回のセッティング

シリーズ第1回兼リンクハブ：

アレンジメント計算 1：確率グラフィカルモデル

因子グラフ、ストリング図へのラベリング

因子グラフの因子ノード／変数ノード、ストリング図のノード／ワイヤーにラベルを付ける際に重要な注意事項があります。それをこの節で述べます。

実数の足し算を、関数 add:R×R → R in Set の形に書きましょう。これを有向因子グラフで描くと次のようです。

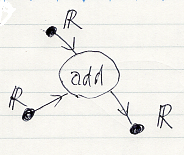
因子グラフの変数ノードには、変数の名前をラベルすることがあります。例えば、addへの入力の変数名が x と y、出力の変数名が z とかです。これを、x:R, y:R, z:R のように書くのが普通でしょうが、コロンは別な目的で使うので、次の約束をします。

変数名をラベルするときは、二重引用符で囲む。例： "x" R
変数名は付けなくてもよい（省略可能だ）が、型（の名前）は必ずラベルする。

この約束に従えば、次のようになります。

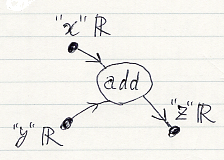
今描いた因子グラフを横1行のテキストで書くときは、add: "x" R, "y" R → "z" R と書くことにします。

ストリング図へのラベリングのときも同じ約束を適用します。

変数名は、理論的な話では不要です。というか、むしろ邪魔です。変数名が必要になるのは、現実をモデリングするときの“分かりやすさ”のためです。名前により意味的情報を付加するわけです。正確な情報ではなくて、あくまで連想による示唆ですが。

後で出てくる「A社の給与の話」で、年齢を入力として年齢手当てを計算する関数が出てきます。これを、f:N → N と書いてしまうと、背後にある意味がまったく伝わりません。f: "年齢" N → "年齢手当て" N とすると、変数名から意味が推測できます（あくまで推測ですが）。

年齢として使う型〈集合〉Nに別名として「年齢」という名前を与え、金額として使う型〈集合〉Nに「金額」という別名を与え、また関数名も「年齢手当て」とすると：

年齢手当て:"年齢" 年齢 → "年齢手当て" 金額

この場合、

入力変数名と入力型名がどちらも「年齢」
関数名と出力変数名がどちらも「年齢手当て」

このようなオーバーロード（言葉の多義的使用）があっても、書き方の約束を守っていれば混同は起きませんが、下手に省略やデフォルトを許すと、名前が何を意味するか分からなくなります。何に対して名前を付けているのか？名前が何を意味するのか？ を常に意識し、そもそも曖昧な書き方は避けるようにしましょう。

アレンジメント、その直感的な導入

アレンジメント〈arrangement〉は、特定の状況における複数の量のあいだの相互依存性〈interdependency〉を記述する図です。アレンジメントの脚〈あし | leg〉がそれぞれの量（の集合）を表すので、n脚アレンジメントはn個の量（の集合）のあいだの相互依存性を示します。

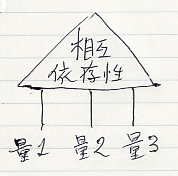
図としてのアレンジメントが表す実体もまたアレンジメントと呼びます。用語「アレンジメント」を、図と実体の意味でオーバーロードするので注意してください。アレンジメントは、確率的状況でなくても使えます。例えば、n脚アレンジメントがn個の集合の直積の部分集合（つまり、n項関係）を表す場合を考えてみましょう。次は、2つのアレンジメント divisor, between の絵です。

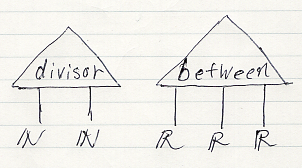
divisor〈約数〉は2項関係、between〈あいだにある〉は3項関係で、次にように定義されます。

divisor := {(n, m)∈N×N | n は m の約数}
between := {(x, y, z)∈R×R×R | x ≦ y ≦ z}

この定義では、divisor⊆N×N、between⊆R×R×R ですが、部分集合に対応する述語（ブール値関数）を考えるなら、次のような写像ともみなせます。

divisor:N×N → {true, false} in Set
between:R×R×R → {true, false} in Set

これから先で考えるアレンジメントは確率的アレンジメント〈probabilistic arrangement〉です。複数の量のあいだの相互依存性が確率的に与えられる場合です。確率というと博打を連想する人がいるかもしれませんが、一般的に、情報の不完全性〈incompleteness〉、不確定性〈uncertainty〉が伴う状況での議論は確率的になります。例えば、とある薬の投与・不投与と病気のとある症状の改善のあいだの相互依存性は確率的アレンジメントになります。

n脚の確率的アレンジメントにおいて、それぞれの脚は集合を表すとします*1。それらを A₁, ..., A_n としましょう。話を簡単にするために、集合は有限集合か可算無限集合とします。脚 A₁, ..., A_n を持つ確率的アレンジメントは、直積集合 A₁×...×A_n から実数区間 [0, 1] への写像 ω:A₁×...×A_n → [0, 1] in Set だとします。ただし、次の条件を満たすことを要求します。

ω(x) ≠ 0 となる x∈A₁×...×A_n は有限個しかない。（A₁×...×A_n が有限集合なら、この条件を気にする必要はありません。A₁×...×A_n が無限集合のときは“大部分”の x で ω(x) は 0 です。）
$\sum_{x \in A_1\times \cdots \times A_n}\omega(x) = 1$ （すぐ上の条件から、A₁×...×A_n が無限集合のときでも総和は有限和になります。）

先の薬の例で、A = {投与, 不投与}, B = {改善有り, 改善無し} として、effect:A×B → [0, 1] in Set を次のように定義しましょう。

effect(投与, 改善有り) = 0.15
effect(投与, 改善無し) = 0.35
effect(不投与, 改善有り) = 0.1
effect(不投与, 改善無し) = 0.4

表の形にしてもいいかも知れません。

effect	投与	不投与
改善有り	15%	10%
改善無し	35%	40%

これは、脚が A, B である確率的アレンジメント effect を定義します。

[補足]
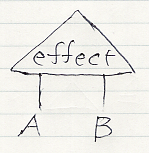
集合Aに「投与」、集合Bに「改善」、アレンジメントに「改善」という名前を付けると、「脚が投与, 改善である確率的アレンジメント改善」となります。このネーミングだと：

集合と要素がどちらも「投与」
集合とアレンジメントがどちらも「改善」

前節で述べた「名前が何を意味するか分からなくなる」現象が起きます。
[/補足]

マルコフ行列

架空の会社A社の給与について考えます。A社は大企業で多数の社員がいるとします。A社では、社員の成果を 1 から 5 の5段階（5が最高）で評価して、それが給与に影響するとします（架空の話ね）。もし、給与が成果ランク（1から5の値）の関数で決定するとすれば、次のように書けます。

給与:"成果" {1, 2, 3, 4, 5} → "金額" N

実際は、決定性の関数ではなくて、確率的非決定性が入るとします。確率的非決定性がある（かも知れない）関数は、矢印「→*」を使って表すことにします。

給与:"成果" {1, 2, 3, 4, 5} →* "金額" N

確率的非決定性がある関数とは何でしょうか？成果ランクの値である 1, 2, 3, 4, 5 のそれぞれに対して、金額の確率分布〈確率測度〉が対応するとしましょう。確率分布とは、各金額の値（自然数としている）の給与をもらっている人の比率です。より詳しく説明するために、関数名／変数名をラテン文字1文字に変えておきます。

S:"r" {1, 2, 3, 4, 5} →* "s" N

r = 1 のときのSの値 S(1) は、N 上の [0, 1] に値を持つ関数で、総和が1です。以下、総和が有限和で済むことは常に仮定します。

S(1):N → [0, 1] in Set
$\sum_{s\in {\bf N}} S(1)(s) = 1$

例えば、S(1)(40万) なら、成果ランクが1で40万の給与をもらっている人の人数を“ランク1の社員総数”で割った値です。S(2), S(3), S(4), S(5) も同じです。

値 S(r)(s) を S(r, s) とも書くことにします。ほんとは、S(r)(s) と書いたときのSと、S(r, s) と書いたときのSは別物（カリー化／反カリー化の関係にある）ですが、大目に見ましょう。{1, 2, 3, 4, 5}×N∋(r, s) $\mapsto$ S(r, s)∈[0, 1] は次の性質を持ちます。

S:{1, 2, 3, 4, 5}×N → [0, 1] in Set
$\forall r\in \{1, 2, 3, 4, 5\}.(\, \sum_{s\in {\bf N}}S(r, s) = 1\,)$

こう書いてみると、Sは無限行5列の行列とみなせます。成分は0以上1以下の実数で、縦列ごとに成分の総和は1です。実際に無限行が必要なわけではなくて、十分大きな自然数Nを取れば、N行5列の行列で十分です（給与の上限値がありますから）。

「成分は0以上1以下の実数で、縦列ごとに成分の総和は1」である行列をマルコフ行列〈Markov matrix〉と呼ぶので、確率的非決定性がある関数とはマルコフ行列だと（とりあえずは）言えます。マルコフ行列 S:"r" {1, 2, 3, 4, 5} →* "s" N をストリング図で次のように図示します。もちろん、変数名は省略してかまいません。

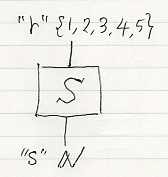
マルコフテンソル

記述を簡略化するために 5 := {1, 2, 3, 4, 5} と置きます。A社の給与は、年齢も影響しているとします。すると、次のように書けます。

T:"r" 5, "a" N →* "s" N

変数名"a"で識別される自然数の集合Nは、年齢を表すものです。これも確率的非決定性がある関数ですが、入力を2つ持ちます。次のように図示します。

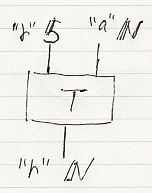
Tの実体は、次のような関数です。

T:(5×N)×N → [0, 1] in Set
$\forall (r, a)\in {\bf 5}\times {\bf N}.(\, \sum_{s\in {\bf N} }T( (r, a), s) = 1\,)$

成果ランクの値 r と年齢の値 a を固定したとき、変数 s の確率分布（集合N上の確率分布）が生じます。

T((r, a), s) は、T(s | r, a) とも書くことにします。縦棒で区切ったこの書き方については「マルコフ核：確率計算のモダンな体系 // 書字順記法と反書字順記法」で説明しています。前節の S(r, s) は S(s | r) とも書きます。

Sは、入力を1つ持つ確率的非決定性関数で次のように書けました。

入出力の仕様： S:"r" 5 →* "s" N
成分： For r∈5, s∈N, S(r, s) = S(s | r)

Tは、入力を2つ持つ確率的非決定性関数で次のように書けます。

入出力の仕様： T:"r" 5, "a" N →* "s" N
成分： For r∈5, a∈N, s∈N, T((r, a), s) = S(s | r, a)

一般に、入力をm個持ち、出力をn個持つ確率的非決定性関数は次のように書けます。

入出力の仕様： F:"x₁" A₁, ..., "x_m" A_m →* "y₁" B₁, ..., "y_n" B_n
成分： For x₁∈A₁, ..., x_m∈A_m, y₁∈B₁, ..., y_n∈B_n, F((x₁, ..., x_m), (y₁, ..., y_n)) = F(y₁, ..., y_n | x₁, ..., x_m)

そして次の条件を満たします。

F:(A₁×...×A_m)×(B₁×...×B_n) → [0, 1] in Set
$\forall x\in A_1\times \cdots \times A_m.(\, \sum_{y\in B_1\times \cdots \times B_n} F(x, y) = 1\,)$

先の書き方の約束から、F(x, y) は F(y₁, ..., y_n | x₁, ..., x_m) とも書かれます。

今定義した“入力をm個持ち、出力をn個持つ確率的非決定性関数”をマルコフテンソル〈Markov tensor〉と呼びます。マルコフ行列が、m = 入力の個数 = 1, n = 出力の個数 = 1 だったのを一般化したものがマルコフテンソルです。

実は（けっこう重要なことですが）、アレンジメント（の実体）はマルコフテンソルの特別な形です*2。薬の効果を表すアレンジメント effect は次のように書けます。

入出力の仕様： effect:() →* "x" A, "y" B
成分： For x∈A, y∈B, effect((), (x, y)) = effect(x, y|)

入力が0個であることを示すために、矢印「→*」の左に () を書いています。effect(x, y|) の縦棒の右には何も書きません。毎回縦棒を書くのはバカバカしいので effect(x, y) と略記するのです。ただし、effect(x, y) は effect(y | x) とも解釈できて曖昧性が生じます。曖昧性を回避するには次のどちらかの約束が必要です。

区切り記号に縦棒だけを使うことにして、effect(x, y) := effect(x, y |) という省略を許す。
区切り記号にカンマも縦棒も許し、省略を許さない。effect(x, y) = effect(y | x) なので、effect((), (x, y)) または effect(x, y|) と書く必要がある。

曖昧性回避のためにどういう約束をするかはケースバイケースですが、我々は主に1番の方法を使います。

マルコフテンソルのプロファイル

引き続き、集合は有限集合か可算無限集合だけを考えます。

マルコフ行列も（確率的な）アレンジメントも、マルコフテンソルの特別なものでした。これらの入出力の仕様を次のように書きました。

S:"r" 5 →* "s" N
T:"r" 5, "a" N →* "s" N
effect:() →* "x" A, "y" B

一般的なマルコフテンソルは：

F:"x₁" A₁, ..., "x_m" A_m →* "y₁" B₁, ..., "y_n" B_n

二重引用符で囲まれた変数名は省略可能なので：

S:5 →* N
T:5, N →* N
effect:() →* A, B
F:A₁, ..., A_m →* B₁, ..., B_n

矢印「→*」を含むマルコフテンソルの入出力仕様を（マルコフテンソルの）プロファイル〈profile〉と呼びます。

本来、マルコフテンソルのプロファイルにおいて、矢印の左右は括弧で囲むべきです。

S:(5) →* (N)
T:(5, N) →* (N)
effect:() →* (A, B)
F:(A₁, ..., A_m) →* (B₁, ..., B_n)

めんどうなので囲み括弧を省略すると：

S:5 →* N
T:5, N →* N
effect: →* A, B
F:A₁, ..., A_m →* B₁, ..., B_n

アレンジメントのプロファイルは effect: →* A, B のように、矢印の左が空になります。分かりにくいので僕は effect: () →* A, B という中途半端な折衷案で表記していました。事情を了解していれば effect: →* A, B でもいいのですが、どうも気持ち悪い（個人の感想です）ので折衷案 effect: () →* A, B にします。

effect(x, y |) の縦棒の省略とか、プロファイルの囲み括弧の省略とか、実に些細な習慣ですが、ある種の不正確さ／曖昧さを招き寄せているのは事実です。些細な不正確さ／曖昧さも積み重なると、深刻な誤謬に繋がるので用心するに越したことはないです。

S:5 →* N のような「→*」を使った書き方は、Sが普通の関数（決定性関数）ではなくてマルコフテンソルであることを示すものですが、さらに事情を明示するために、次の書き方も使います。

S:5 →* N in MarkovTens

MarkovTens はマルコフテンソル達の世界のことで、Sがその世界の住人であること明示しています*3。

アレンジメントの組み立て方

再び、A社の給与について考えます。給与に関しては、「何によって／どのように、給与が決まるのか？」に興味がいくでしょうが、とりあえずは入力と出力の区別をせずに、相互依存しそうな量を列挙してみます。

成果 "r" 5
年齢 "a" N
性別 "g" Gend （Gend = {male, female}）
給与 "s" N

これらの量が相互依存している（かも知れない）状況は次のアレンジメントαとして図示されます。

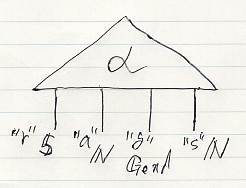
アレンジメントの（マルコフテンソルとしての）プロファイルは：

α: () →* "r" 5, "a" N, "g" Gend, "s" N in MarkovTens

変数名を取り除けば：

α: () →* 5, N, Gend, N in MarkovTens

αの実体は：

α:1×(5×N×Gend×N) → [0, 1] in Set
$\forall x \in {\bf 1} .(\, \sum_{ (r, a, g, s) \in {\bf 5} \times {\bf N} \times {\bf Gend} \times {\bf N} } \,\alpha(r, a, g, s \mid x) = 1 \,)$

1 = {1} は選ばれた単元集合〈distinguished singleton set〉です*4。 $\forall x \in {\bf 1}$ という限量子は実質的な意味はないので削り落とします。 $\alpha(r, a, g, s \mid x)$ の $x$ の値は単元集合の唯一元なので、明示的には書かずに、さらに縦棒を省略して：

$\sum_{ (r, a, g, s) \in {\bf 5} \times {\bf N} \times {\bf Gend} \times {\bf N} } \,\alpha(r, a, g, s) = 1$

このαは、A社の全社員に関するデータを、空間 5×N×Gend×N 上の比率値の分布*5として表現したものです。空間全体に渡る総和が 1 なので確率分布です。αには入力と出力の別（あるいは原因と結果の別）はありません。4つの量を対等に扱い、それらの量のあいだの相互依存性（場合により非依存性）を記述しているだけです。

アレンジメントαの背後には、A社の給与制度がメカニズムとして存在します。そのメカニズムは次のようだとしましょう。

確率的非決定性関数 S:5 →* N in MarkovTens で成果給が決まる。
決定性関数 f:N → N in Set で年齢手当てが一意的に決まる。これは年齢だけで一律に計算される。
成果給と年齢手当てが足し算される。
性別は給与にまったく影響しない（A社は男女平等です）。

結局、成果と成果給の関係性だけに不確定性が入り、年齢と年齢手当ては決定性、性別と給与は無関係〈独立〉です。

以上の状況を絵に描くために、次の約束をしましょう。

決定性関数 f:N → N in Set に対して、マルコフテンソル δ(f):N →* N in MarkovTens を次のように定義する。
- δ(f)(t | a) := eq(t, f(a))
- eq(x, y) は、x = y のとき 1、その他は 0 となる関数。
add:N×N → N in Set は足し算関数。δ(add) は上と同じ手順で N, N →* N in MarkovTens とみなした足し算。
任意の集合Xに対して、!_X:X →* () in MarkovTens は、このプロファイルで唯ひとつ存在するマルコフテンソル。

これらの記法を使うと、確率的非決定性関数〈マルコフテンソル〉 β:"r" 5, "a" N, "g" Gend →* "s" N は次のように描けます。右端の黒丸は !_Gend:Gend →* () in MarkovTens です。

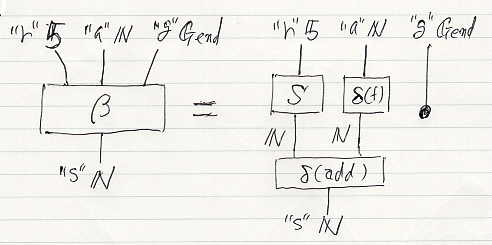
アレンジメントαは、マルコフテンソルβを“同時化”したものです。同時化は説明してませんが、絵ではワイヤーを曲げることです*6。

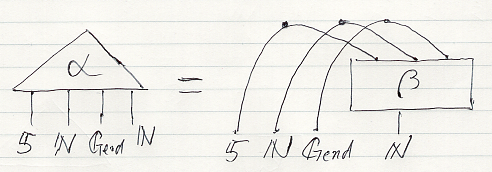
上の絵は、いわば「αの種明かし」になっています。現実には観測データとしてブラックボックスであるアレンジメントが与えられて、未知のメカニズムを推測することが多いでしょう。その場合、アレンジメントのメカニズム、つまり組み立て方や内部構造を記述する手段がないと何も出来ません。アレンジメント図、より一般にはストリング図がその記述手段を与えてくれます。

今回のセッティング

圏論的確率論を具体的に展開するには、具体的に構成されたマルコフ圏Cと、Cの標準簡約多圏Pをベースにします。今回のケースでは、マルコフ圏Cを次のように作ります。

集合圏Set上の{形式的}?凸結合モナド Convex を考える。凸結合モナドについては、「質点系の重心、形式的凸結合のモナド」参照。
凸結合モナドのクライスリ圏 Kl(Set, Convex) を作る。
Kl(Set, Convex) のなかで、有限集合と可算無限集合だけに制限した充満部分圏をCとする。
Cにマルコフ圏の構造を与えるのは容易。

圏Cの射はマルコフ行列とみなせます。対象を集合から“集合のリスト”に拡張して、ホムセットはCのホムセットを使うように構成すると、Cの標準簡約多圏Pが作れます。詳細は「対称モノイド多圏（簡約版）」参照。

Pの対象は集合のリストで、射はマルコフテンソルです。つまり、P = MarkovTens。図としてのアレンジメントを P = MarkovTens で解釈すれば、脚（ワイヤーの並び）が集合のリストで、三角ノードは域が空リストであるマルコフテンソルに対応します。

今回の C, P は、構成に測度論をまったく必要とせず、計算は積分ではなくて有限和だけで済みます。予備知識を必要とせず、実用にもそこそこ使えるので、なかなか良いセッティングだと思います。（[追記]「アレンジメント計算 7： AlmostSurelyEqual // 事例に関して」に続きがあります。[/追記]）

*1:ここでは、可測空間の代わりに集合を用います。

*2:抽象的一般論では、図としてのアレンジメントは、マルコフ多圏における“単位対象からの射”を表します。

*3:概念的事物が住んでいる世界・場所をアビタ〈habitat (フランス語)〉といいます。住人・居住地のような比喩的言い回しは、ヨーロッパの型理論のコミュニティで使われているようです。

*4:単元集合なら何でもいいのですが、1 = {0} という定義のほうが多いかも。

*5:経験分布と呼ばれるものです。有限個の点以外での値は0で、比率である値（凸結合の係数）は有理数です。

*6:ストリング図でワイヤーを曲げる操作は色々な場面で登場します。デカルト閉圏におけるカリー化／反カリー化、トレース付き圏のトレース、コンパクト閉圏の単位・余単位など。そして、ワイヤー曲げが重要なオペレーションとなります。