「反ラックス・モノイド関手の一般余結合律」における二分木〈バイナリーツリー〉の扱いが不十分だったので補強します。目的の計算を実行するために*1、色々と準備が必要ですな。
内容:
- 最初の記事(シリーズ目次あり): 準マルコフ圏からなる2-圏
- 次の記事: 反ラックス・モノイド余モナド: 記号の使用・乱用 再考
- 前の記事: 反ラックス・モノイド余モナドの余クライスリ圏 その1
目論見違い
「反ラックス・モノイド関手の一般余結合律」から幾つかの文言を引用します。
二分木の全体をオペラッドに仕立てることは出来ますが、意外とめんどくさいので、今回は半オペラッドでよいとします。
今回は、上段にある
(左からのスイッチと右からのスイッチ)という基本変形だけを使うので、下段の変形は無視してください。
ちょっと細工すると、
を関手とみなすことが出来ますが、今はこれ以上触れません。「ツリー書き換え系とマックレーンの一貫性定理」を参照してください。
我々の目的である準マルコフ余モナドの計算で必要になるのは、幾つかの個別具体ケースで、ほんとに一般的な余結合律が必要なわけではありません。
要するに、「後で使う予定がないものは省くよ」ということでした。しかし、これは僕の目論見違いで、やはりチャンとやらないとダメみたいです。
二分木達が持つ構造をチャンと理解するために、考察の範囲を二分木からBUNツリー〈binary-unary-nullary tree〉に広げて、オペラッド構造と亜群構造を定義することにします。
この記事は、過去記事「ツリー書き換え系とマックレーンの一貫性定理」の一部を切り出してリバイスしたものになります。
BUNツリー
二分木〈バイナリーツリー〉は、二股に分かれる分岐ノードだけを持ちます。枝分かれしないノードと行き止まりのノードも認めたツリーを考えましょう。ノードを演算子記号だと解釈するなら、二項演算子記号〈binary operation symbol〉以外に、単項演算子記号〈unary operation symbol〉と無項演算子記号〈nullary operation symbol〉も認めることになります。なので、これから考えるツリーをBUNツリー〈BUN tree | binary-unary-nullary tree〉と呼びます。
BUNツリーのテキスト表示のために、次の記号を使います。
正確な構文ルールを述べなくても、いくつかの例を見ればBUNツリーのテキスト表示は分かるでしょう。
丸括弧の省略はしないことにします。「反ラックス・モノイド関手の一般余結合律」のように、プレースホルダーに番号は要求しませんが、必要なときは左から右の順で番号を付けることができます。例えば:
「反ラックス・モノイド関手の一般余結合律」では黒丸 を使いましたが、今回は楔形〈くさびがた〉
です。これは「ツリー書き換え系とマックレーンの一貫性定理」と同じ記法に戻したのですが、“象形文字”になっています。記号列表現から割と容易に図形をイメージできるでしょう(下図参照)。
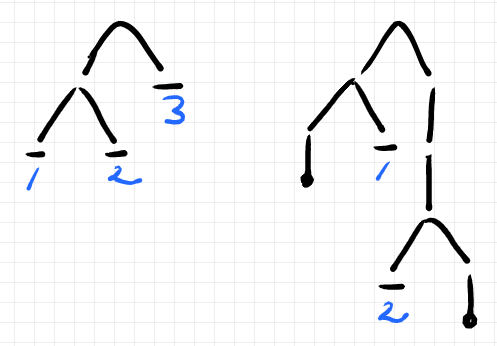
BUNツリーの末端〈葉〉のプレースホルダーの個数をBUNツリーの幅〈width〉と呼び と書きます。例えば:
最も基本的なBUNツリーの幅は次のようです。
伸縮同値関係
BUNツリー があると、
を作ることができます。また、
に対して、
番目のプレースホルダーに
を代入した〈置換した〉
を作ることができます。(置換演算に関しては「反ラックス・モノイド関手の一般余結合律」参照。)
は
をルート方向に伸ばした形になり、
は
をリーフ方向に伸ばした形になります。このような
による伸長〈expansion〉をしても元のツリーと変わらないとみなします。ルート方向/リーフ方向に限らず、中間の位置に
を挿入してもツリーとしては同じだとします。
もう少し詳しくいうと、BUNツリー の適当な位置に
を追加・挿入して得られたBUNツリーが
であるとき、
と書くことにします。BUNツリーのあいだの二項関係
を含む最小の同値関係を
として、伸縮同値関係〈expansion-and-contraction equivalence relation〉と呼びましょう。
伸縮同値なBUNツリーの例を幾つか挙げると:
BUNツリーを図形として捉えるとき、無意識に伸縮同値関係は前提しているのではないでしょうか。以下では、BUNツリーというとき、伸縮同値関係の同値類、または同値類の代表元を指しているとします。つまり、伸縮同値な2つのBUNツリーは同一視するということです。
オペラッド=複圏
BUNツリー(の伸縮同値類)の全体はオペラッド〈operad〉になります。オペラッドは複圏〈multicategory〉とも呼ばれます。複圏の用語を使うと、通常の圏との対応が分かりやすいでしょう。
| 圏 | 複圏〈multicategory〉 |
|---|---|
| 対象 | 複対象〈multiobject〉 |
| 射 | 複射〈multimorphism〉 |
| ホムセット | 複ホムセット〈multihomset〉 |
| 結合 | 複結合〈multicomposition〉 |
BUNツリーの場合は:
- 複対象は自然数
- 複射はBUNツリー
- 複ホムセットは同じ幅を持つBUNツリーの集合
- 複結合はツリーの接ぎ木〈置換演算〉
複圏〈オペラッド〉としてのBUNツリー(の伸縮同値類)の全体を と書くことにします。幅が
のBUNツリーのプロファイルは、
と書けます。複ホムセットを
と書けば、
です。BUNツリーの余域〈codomain〉は常に 1 なので*2、複ホムセットは
と略記します*3。
複結合〈オペラッド結合〉は、「反ラックス・モノイド関手の一般余結合律」で紹介した代入〈置換演算〉、あるいは接ぎ木〈grafting〉です。次の2つのケースが特によく使います。
- 単一複結合〈single multicomposition〉*4 : 2つのBUNツリー
と 自然数
に対して定義される
。
- 全複結合〈total multicomposition〉 : BUNツリー
と
個のツリー
に対して定義される
全複結合の場合は、次のような略記を使ってもかまいません。
複結合の記法は反図式順なので、図式順記法も準備しておきます。 は置換リスト〈代入リスト〉です。
複圏〈オペラッド〉の議論だと、複結合が複雑なので、図式順・反図式順の食い違いによる混乱も複雑になるので注意が必要です。
なお、複圏〈オペラッド〉に関する入門的解説は「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」にあります。
オペラッド=複圏の法則
BUNツリーに対する複結合は、伸縮同値類の代表元によらずに定義できるので、伸縮同値類の集合(商集合)上で定義された演算と考えます。BUNツリーに対する操作は、常に「伸縮同値類の代表元によらずに定義できる」ことが要求されますが、今後イチイチ言及はしないでしょう。
圏の場合と同様に、複圏〈オペラッド〉の複結合に対しても法則があります。複結合として、単一複結合をとるか/全複結合をとるか/それとも任意の置換演算をとるかにより、法則の記述も変わってきます。ここでは、法則の記述が簡単になるように、単一複結合に対して法則を述べます。
これらは複結合に対する結合律と単位律です。それとは別に という表現に意味を持たせるために次も必要です。
等式は、伸縮同値類に対するものです。もし、伸縮同値関係で商をとる前のBUNツリーに関して法則を述べるならば次のようです。
これらは直感的には明らかですが、キチンとした組み合わせ的議論はけっこう面倒です。割愛します。
単一複結合に関する法則を繰り返し適用することにより、全複結合に対する結合律・単位律、任意の置換演算に対する結合律・単位律を示すことができます。
複ホムセットの亜群構造
圏に対して豊饒圏〈豊穣圏 | enriched category〉があるのと同様に、複圏〈オペラッド〉に対して豊饒複圏〈enriched multicategory〉があります。つまり、複ホムセットが単なる集合ではなくて圏の対象になるということです。ここで考える豊饒化〈enriching〉は、亜群豊饒化です。亜群〈groupoid〉とは、(小さい)圏であって、すべての射が可逆なものです。
BUNツリーの複圏の複ホムセット に亜群構造を入れましょう。この亜群構造は、「ツリー書き換え系とマックレーンの一貫性定理」で述べたものです。「反ラックス・モノイド関手の一般余結合律 // 二分木の変形」でも繰り返しているので、ここでは用語と記法の約束だけ確認します(以前と少し変更します)。
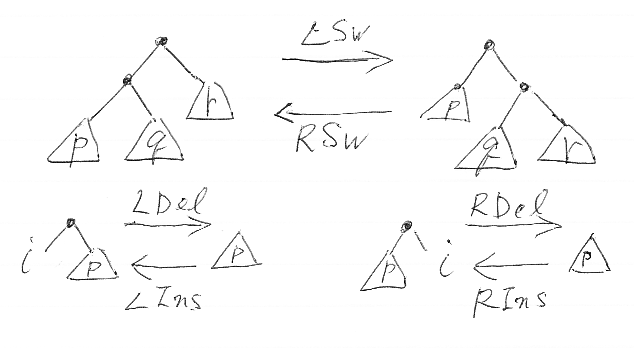
4種類の基本変形は:
]
以下の絵は「ツリー書き換え系とマックレーンの一貫性定理」に載せたもので、プレースホルダーの下にサブツリーをぶら下げた形に描いています。
これらの変形を、ツリーの任意の部分に許した変形が単純変形です。単純変形の順次実行が(一般の)変形〈{transformation | rewrite | deformation | move}〉ですが、順次実行はBUNツリーと単純変形を代わりばんこに並べたリスト で表します*5。恒等変形は
です。
さて、今まで/ここまで、単に「変形」という言葉を使ってきたのですが、我々の変形はかなり特殊なものです。何の形容詞も付けないのはマズイ気がしてきたので、このテの変形に注目してモノイド圏の一貫性理論を構築したマックレーン〈Saunders Mac lane〉の名前を冠して、マックレーン基本変形/マックレーン単純変形/マックレーン変形と呼ぶことにします。
マックレーン変形の亜群としての(圏としての)結合は図式順結合記号 で表すことにします。反図式順なら
です。亜群結合はリスト表示では連接になります(繋ぎ目になった重複するツリーを取り除きますが)。
マックレーン基本変形は、互いに逆な3組のペアでした。
これらの逆関係は、マックレーン単純変形にも引き継がれて、マックレーン変形の逆は次のように与えられます。
以上の定義により、 の複ホムセットにマックレーン変形の集合を一緒にすると亜群となります。以下では、亜群構造も含めて
と書くことにします、複ホムセットはもはや単なる集合ではありません、複ホム亜群〈multihom-groupoid〉です。亜群は圏なので次の記法を使います。
: 幅
のすべてのBUNツリー(の伸縮同値類)の集合
: BUNツリー
から
へのすべてのマックレーン変形の集合
: BUNツリー
の恒等マックレーン変形
: マックレーン変形
と
の亜群結合
混乱・混同を避けるために、マックレーン変形のプロファイルは引き続き波矢印を使って と書くことにします。
複結合が亜群準同型射になること
2つの複ホムセット のあいだには、単一複結合の演算
があります。
前節で述べたごとく、複ホムセットは今や複ホム亜群です。単一複結合は、対象であるBUNツリーに対してだけでなく、亜群射であるマックレーン変形に対しても定義する必要があります。次の赤い二重疑問符の部分を埋めなくてはなりません。
マックレーン変形の単一複結合〈オペラッド結合〉 の定義を、組み合わせ的に厳密に述べるのは難しいですが、直感的には簡単な話です。絵を描いてお茶を濁しておきます。
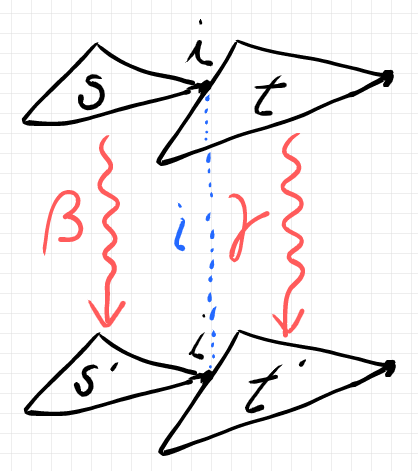
マックレーン変形は、BUNツリーのプレースホルダー(ツリーの葉)の個数や位置を変えることはありません。ツリー内部の繋がり方は変わっても“輪郭”は不変です。 番目のプレースホルダー(接合点)で繋がれたそれぞれのBUNツリーにそれぞれのマックレーン変形を施すと、全体もマックレーン変形になります。それがマックレーン変形の単一複結合〈オペラッド結合〉
です。
以上で(直感的ですが)、対象であるBUNツリーの複結合と射であるマックレーン変形の複結合が定義できました。この定義は、亜群の準同型写像である必要があります。「単一複結合が亜群の準同型写像である」ことを書き下すために、 という記法も使います*6。
の域は直積亜群です。直積亜群の亜群結合と亜群恒等は次のような単純な定義です。
が亜群の準同型写像、つまり関手であることは次のように書けます。
あるいは、
を中置演算子記号
に書き換えれば:
これは、モノイド圏/2-圏などで見慣れた交替律〈interchange law〉です。BUNツリー(1次元複射)の複結合〈オペラッド結合 | 置換演算 | 代入〉 を横結合、BUNツリーのマックレーン変形(2次元射)の亜群結合
を縦結合とみなして、縦横の演算が協調することを示しています。雰囲気的な図式を描けば:
交替律も直感的には自明に思えるのですが、組み合わせ的・帰納的議論で示すべきでしょう -- そのテの話を詳しくするが目的ではないで今回は省略します。
BUNツリーとマックレーン変形が作る構造
今まで述べたことにより は、単なるBUNツリーの集合ではなくて、マックレーン変形も含む構造になっています。これは、0次元、1次元、2次元の構成素を含む圏論的構造物と考えることができます。
BUNツリー、例えば のプロファイルは
のように書けます。自然数
の意味はプレースホルダーが2個あることなので、
と書いてもいいでしょう。プレースホルダーが基本的な0次元構成素=基本対象で、それを幾つか並べたリストが複対象、BUNツリーが1次元構成素=複射、マックレーン変形が2次元の構成素です。
複ホムセットごとに亜群構造が入り、その亜群構造は複結合〈オペラッド結合 | 置換 | 代入〉と協調します。つまり、亜群豊饒化〈豊穣化 | enriching〉された複圏〈オペラッド〉です。この構造を短く亜群複圏〈groupoid-multicategory〉または亜群オペラッド〈groupoid-operad〉と呼ぶことにします。
亜群オペラッド のマックレーン変形は、ある種の2-射なので、そのプロファイルは次のようにも書きます。
もう少し簡潔に書くと:
この書き方だと、マックレーン変形が2次元の構成素で、プレースホルダーが0次元の構成素であることが強調されませんが、簡潔なのはメリットです。
亜群オペラッドとしての は、モノイド圏の計算のための計算デバイスとして重要です。モノイド圏
が与えられたとき、亜群オペラッドの構成素を
に関して解釈することができます。その解釈方法は引き続く記事で述べます。