世間では、自然言語で会話できるチャットAI/大規模言語モデルの話題が盛り上がってますが、僕にとっての当面の期待は、人間可読でありながら機械可読でもある形式的証明記述の可能性です。長年のストレスであった次のジレンマが解決するかも知れません。
- 機械可読なタクティク証明は人間が読めない。対人間の解説・説明には使えない。
- 人間向けの自然言語混じりの非形式的証明は機械可読ではないので、機械的検証は出来ない。
人間可読かつ将来的には機械可読(となると期待できる)運算的証明形式〈calculational proof format〉については、「近未来の証明ソフトウェアはこうなる(といいな)」に書きました。この記事では、運算的証明フォーマットより広い範囲で使えると思われるヤシコフスキ/カリシュ/モンタギュー形式〈Jaśkowski-Kalish-Montague format〉の証明について述べます。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\letsShow}{\Keyword{lets show } }
\newcommand{\conclude}{\Keyword{conclude } }
\newcommand{\endBlock}{\Keyword{end } }
\newcommand{\assume}{\Keyword{assume } }
\newcommand{\Imp}{ \Rightarrow }`$
内容:
例題
まず最初に、ヤシコフスキ/カリシュ/モンタギュー形式の証明の事例を挙げます。
$`p, q, r`$ は命題だとして、$`( (p \Imp q) \land (\lnot r \Imp \lnot q) )\Imp (p \Imp r)`$ という論理法則の証明です。証明ソースコード中に登場する日本語の文言はコメントではなくて、証明の正式な一部であり、将来的には機械〈ソフトウェア〉可読であると想定します。$`\cdots \text{(番号)}`$ の部分は後の説明のためで、実際には不要です。
$`\letsShow ( (p \Imp q) \land (\lnot r \Imp \lnot q) )\Imp (p \Imp r)\\
\bullet (p \Imp q) \land (\lnot r \Imp \lnot q) \text{ を仮定して、 } (p \Imp r) \text{ を導く}\\
\quad \assume (p \Imp q) \land (\lnot r \Imp \lnot q) \:\cdots \text{(1)}\\
\qquad \letsShow p \Imp r\\
\qquad \bullet p \text{ を仮定して }r \text{ を導く}\\
\qquad\quad \assume p \:\cdots \text{(2)}\\
\qquad\qquad \downarrow \text{上の仮定を再掲}\\
\qquad\qquad (p \Imp q) \land (\lnot r \Imp \lnot q) \:\cdots \text{(3)}\\
\qquad\qquad \downarrow \text{すぐ上の連言の左側}\\
\qquad\qquad p \Imp q \:\cdots \text{(4)}\\
\qquad\qquad \downarrow \text{モーダスポネンスを適用}\\
\qquad\qquad q \:\cdots \text{(5)}\\
\qquad\qquad \downarrow \text{上の連言の右側}\\
\qquad\qquad \lnot r \Imp \lnot q \:\cdots \text{(6)}\\
\qquad\qquad \letsShow r\\
\qquad\qquad \bullet \text{背理法を使う}\\
\qquad\qquad\quad \assume \lnot r \:\cdots \text{(7)}\\
\qquad\qquad\qquad \downarrow\text{先の命題を再掲}\\
\qquad\qquad\qquad \lnot r \Imp \lnot q \:\cdots \text{(8)}\\
\qquad\qquad\qquad \downarrow \text{モーダスポネンスを適用}\\
\qquad\qquad\qquad \lnot q \:\cdots \text{(9)}\\
\qquad\qquad\qquad \downarrow\text{先に得られた命題を再掲}\\
\qquad\qquad\qquad q \:\cdots \text{(10)}\\
\qquad\qquad\qquad \downarrow\text{矛盾が生じる}\\
\qquad\qquad\qquad \bot\\
\qquad\qquad\quad \endBlock\\
\qquad\qquad \conclude r\\
\qquad\quad \endBlock\\
\qquad \conclude p \Imp r\\
\quad \endBlock\\
\conclude ( (p \Imp q) \land (\lnot r \Imp \lnot q) )\Imp (p \Imp r)
`$
ゲンツェンとヤシコフスキ
これから述べる歴史的な話と図版は次の論文にもとづいています。
- Title: Kalish/Montague and Ja´skowski Natural Deduction
- Authors: Mohammad M. Ajallooeian, Francis Jeffry Pelletier
- Pages: 9p
- URL: https://mirror.las.iastate.edu/tex-archive/macros/latex/contrib/natded/extended_doc.pdf
ゲンツェン〈Gerhard Gentzen〉は1934年の論文で自然演繹を導入しました。ゲンツェンの証明図はツリーの形をしています。文字組版技術でもレイアウトできるように、横棒を使って描きます。
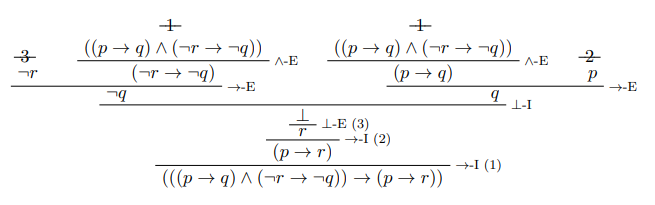
横棒を使ったツリーの証明図は、論理の教科書ではよく見ます。
奇しくも同じ年1934年に、ヤシコフスキ〈Stanisław Jaśkowski〉も形式的証明と証明図のアイディアを発表します。ヤシコフスキの証明図は入れ子のボックスを使ってレイアウトします。これも、罫線文字を使った文字組版技術でぎりぎり描けそうです。

後年、カリシュ〈Donald Kalish〉とモンタギュー〈Richard Montague〉は、書籍"Logic: Techniques of Formal Reasoning"のなかでヤシコフスキ流証明図を少しだけ変更して使用します。

カリシュ/モンタギュー形式では、これから証明すべき命題をキーワード $`\text{Show}`$ に続けて宣言します。その命題の証明が終えたら、$`\text{Show}`$ を取り消し線で消します。完了した証明では、すべての $`\text{Show}`$ が取り消されています。
ヤシコフスキ/カリシュ/モンタギュー形式の証明図を、テキストだけ(ただしカラーリングはしている)で表現したものが前節に挙げた事例です。$`\text{Show}`$ の代わりに、$`\letsShow`$ として、$`\letsShow`$ で提示したターゲット命題の証明が終わる場所に $`\conclude`$を置いています。
$`\letsShow\cdots\:\conclude`$はブロック構造ですが、他に $`\assume\cdots\:\endBlock`$のブロック構造も使っています。これらのブロック構造がヤシコフスキのボックスの代わりです*1。
自然言語ヒント
今までの(今日の時点では現状の)証明ソフトウェアでは、タクティクではない宣言的証明記述〈declarative proof description〉であっても、次の事は大きな負担となる難点でした。
- 推論の根拠を示すために、「上の」「先の」「前述の」などの曖昧な指示語が使えないために、行番号やラベルを付けて命題や宣言を参照する必要がある。
- 「背理法を使う」「待遇を示す」「数学的帰納法を使う」のような方針を示す言葉はソフトウェアに通用しないので、それ専用のコマンドや構文を憶えて、正しい構文で書く必要がある。
- 連言〈論理AND〉の左側を取るような、簡単な操作も、いちいち正確な推論規則を指定しなくてはならない。
- 「分配法則により」「モーダスポネンスを使って」「群の準同型定理から」のような言い回しもソフトウェアは理解しないので、ライブラリ/パッケージ内で使われている正確な綴り〈例えば
Rat.distribSMul〉を憶えているか、知らないなら試行錯誤とgrepでライブラリ/パッケージ内を検索する必要がある。
これらの問題点は、ソフトウェアによる自然言語理解と検索機能により解決されるでしょう(そう期待している)。
例題に出てくる日本語ヒントを(人間なら分かるでしょうが)解説しておくと:
- 上の仮定を再掲 : 「上の仮定」は命題(1)のこと。
- すぐ上の連言の左側 : 「すぐ上の連言」は命題(3)のこと。「左側」は $`p⇒q`$ 。
- モーダスポネンスを適用 : 命題(4)と命題(2)に対しての適用。
- 上の連言の右側 : 「上の連言」は命題(3)、「右側」は $`\lnot r \Imp \lnot q`$
- 先の命題を再掲 : 「先の命題」は命題(6)
- モーダスポネンスを適用 : 命題(8)と命題(7)に対しての適用。
- 先に得られた命題を再掲 : 「先に得られた命題」は命題(5)。
- 矛盾が生じる : 命題(9)と命題(10)から $`\lnot q \land q`$ なので矛盾。
他にも、「‥‥を仮定して‥‥を導く」とか「背理法を使う」などの自然言語の文言(語句や文法は非常に簡単)もソフトウェアには全く通じないものでした(現時点では「通じないものです」)。
Mizarのような人間可読性が高い証明記述言語(「Mizar証明の抜群な分かりやすさ」参照)でも、上に挙げたような問題があるために、「やっぱり使いものにならない」というのが実感でした。
証明ソフトウェアが自然言語ヒントを理解して、(ライブラリ検索のような)人間にはつらく時間がかかる作業を代行してくれるなら、「使いものになる」ソフトウェアになると期待しています。
今まで「このくらいの事はそのうち出来るようになるだろ」と甘い予測と期待をしては外してきたのですが、今度こそ「このくらいの事はそのうち出来るようになる」といいなぁ。
*1:追記: lets show 、assume を含めて全部で5種類のブロックがあれば自然演繹の証明は書けます。利便性からブロックの種類を増やすことはあるでしょうが、基本は5種類で十分です。