「ヴォエヴォドスキーの宇宙圏とパルムグレンの複前層」で述べたように、ヴォエヴォドスキーとパルムグレンは、同じ時期に同じ概念を独立に考えていたようです。その概念を、パルムグレンによる呼び名 "multivariable presheaf over $`\mathcal{C}`$" を縮めて「$`\mathcal{C}`$ 上の複前層〈multi-presheaf over $`\mathcal{C}`$〉」と呼ぶことにします(過去記事で既にそう呼んでます)。
$`\mathcal{C}`$ 上の複前層達の圏 $`\mathrm{MPSh}(\mathcal{C})`$ は、それ自身がC-システム(「C-システム、分裂ディスプレイクラス、カートメルツリー構造」参照)になるだけでなくて、他の型理論的圏(「指標の圏はコンテキストの圏の反対圏」参照)をホストする環境にもなります。例えば、ファミリー付き圏(の下部構造)を長さ2の複前層として定義できます。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\In}{\text{ in }}
\newcommand{\base}[1]{ {{#1}\!\lrcorner} }
%\newcommand{\Imp}{\Rightarrow}
%\newcommand{\Iff}{\Leftrightarrow}
%\newcommand{\u}[1]{\underline{#1}}
\newcommand{\op}{ \mathrm{op} } % used
\newcommand{\hyp}{\text{-} } % used
%\newcommand{\id}{ \mathrm{id} } % used
`$
内容:
複前層の書き方
複前層については以下の記事で説明しています。
上記の記事内で、複前層達の圏 $`\mrm{MPSh}(\cat{C})`$ の対象(複前層)を次のように書いていました。
$`\quad \vec{P} = [P_1, \cdots, P_n]`$
この書き方は、パルムグレンの論文を踏襲したものです。$`\cat{C}`$ は了解されているとして省略しています。
$`\cat{C}`$ を明示した別な書き方も使うことにします。
$`\quad \vec{P} = (\cat{C} \mid P_1, \cdots, P_n)`$
長さ 0 、長さ 1 のときは次のようです。
$`\quad (\cat{C} \mid)\\
\quad (\cat{C} \mid P)
`$
$`\cat{C}`$ を省略した場合は丸括弧を角括弧〈ブラケット〉にすると約束すれば、以前の書き方と互換性を保てます。
複前層 $`\vec{P}`$ に対する $`\sigma_\cat{C}(\vec{P})`$ は、実は繰り返しグロタンディーク構成でした(「パルムグレンによる、型理論の複前層モデル」参照)。0回、1回の繰り返しも含めた繰り返しグロタンディーク構成を、次の書き方をすることにします。
- $`\int (\cat{C}\mid) := \cat{C}`$
- $`\int (\cat{C}\mid P) := \int_\cat{C} P`$
- $`\int (\cat{C}\mid P_1, P_2) := \int ( \int (\cat{C}\mid P_1) \mid P_2)`$
- 以下同様
以前の書き方との関係は:
$`\quad \sigma_\cat{C}(P_1, \cdots, P_n) = \int(\cat{C} \mid P_1, \cdots, Pn)`$
複前層の長さによる階付け
複前層 $`\vec{P}`$ には長さ $`\ell(\vec{P})`$ が決まっています。この長さに基づいてカートメルツリー構造(「C-システム、分裂ディスプレイクラス、カートメルツリー構造」参照)が入り、複前層の圏 $`\mrm{MPSh}(\cat{C})`$ はC-システムになります。
複前層の圏を $`\mrm{M}^\cat{C}`$ と短く書いてもいいとしましょう。長さが $`n`$ の対象達を含む充満部分圏を $`\mrm{M}^\cat{C}_n`$ と書くことにします。対象の集合 $`|\mrm{M}^\cat{C}_n|`$ は、$`|\mrm{M}^\cat{C}|_n`$ とも書きます。すると、複前層の圏は階付けされた圏〈graded category | 階付き圏〉となり、対象達の集合は階付けされた集合〈graded set | 階付き集合〉となります。
射達の集合 $`\mrm{Mor}(\mrm{M}^\cat{C})`$ には、次のような二重の階付けをします。
$`\quad \mrm{Mor}(\mrm{M}^\cat{C})_{n, m} :=
\{ f\in \mrm{Mor}(\mrm{M}^\cat{C}) \mid \ell(\mrm{dom}(f)) = n \;\land\; \ell(\mrm{cod}(f)) = m
\}
`$
記号が煩雑になるので、次の略記をします。
$`\quad \mrm{M}^\cat{C}_{n, m}:= \mrm{Mor}(\mrm{M}^\cat{C})_{n, m}`$
不等号を使った次のような書き方もします。意味は明らかでしょう。
$`\quad \mrm{M}^\cat{C}_{\le n}\\
\quad \mrm{M}^\cat{C}_{\le n, \le m}
`$
$`{\bf 1}`$ を、単一の対象と恒等射だけの自明圏とします(単元集合の名前とオーバーロードしてます)。$`\mrm{M}^{\bf 1}`$ は、一番簡単な複前層の圏ですが、十分に興味深い圏です。
- $`\mrm{M}^{\bf 1}_1`$ は、集合圏 $`{\bf Set}`$ と同型な圏である。
- $`\mrm{M}^{\bf 1}_{\le 1}`$ としても、特定された終対象 $`[ ] = ({\bf 1}\mid)`$ が追加されるだけ。
- $`\mrm{M}^{\bf 1}_2`$ は、ファミリー〈indexed family of sets〉達の圏と同型な圏になる。
$`\mrm{M}^{\bf 1}_{\le 2}`$ のなかに、ファミリーの圏、集合圏、自明圏が詰め込まれています。一番簡単な複前層の圏の長さ2以下の部分だけでも豊富な構造を持つわけです。
ファミリー付き圏
ファミリーを対象として、ファミリーのあいだの準同型射を射とする圏を $`{\bf Fam}`$ とします。前節で述べたように、$`{\bf Fam} := \mrm{M}^{\bf 1}_2`$ と定義できますが、直接的な定義をしましょう。
集合 $`X`$ に対して、圏 $`{\bf Fam}[X]`$ は次のような関手圏です。
$`\quad {\bf Fam}[X] := {\bf CAT}( (X \text{ as cat}), {\bf Set}) \;\In {\bf CAT}`$
ここで、$`(X \text{ as cat})`$ は、集合を離散圏とみなしたものです。関手圏の射、つまり自然変換がファミリーのあいだの準同型射となります。
ファミリーの域〈インデキシング集合 | ベース集合〉$`X`$ を動かして、グロタンディーク構成で寄せ集めたものがファミリーの圏です。
$`\quad {\bf Fam} := \int_{x: {\bf Set}} {\bf Fam}[x]`$
グロタンディーク構成(シグマ型の圏バージョン)の標準射影は、ファミリーの域〈インデキシング集合〉をとる関手になるので、次のように書きます。関手であることを強調して大文字始まりにしています。
$`\quad \mrm{Dom}: {\bf Fam} \to {\bf Set} \In {\bf CAT}`$
さて、ディビエ〈Peter Dybjer〉により定義されたファミリー付き圏〈category with families | CwF〉は、型理論的圏なので拡張包括構造(「拡張包括構造のもうひとつの定式化」参照)を持ちますが、下部構造として、小さい圏 $`\cat{C}`$ と次のような反変関手 $`T`$ を備えています。
$`\quad T:\cat{C}^\op \to {\bf Fam} \In {\bf CAT}`$
今回は、ファミリー付き圏〈CwF〉の下部構造である $`(\cat{C}, T)`$ だけに注目します。$`(\cat{C}, T)`$ は、長さ 2 の複前層とみなせます。そのことを次節で説明します。
複前層としてのファミリー値反変関手
前節の $`T`$ は、ファミリー(と準同型射)を値とする反変関手なので、ファミリー値反変関手と呼ぶことにします(ファミリー値前層と呼んでもいいかも知れません)。言いたいことは、ファミリー値反変関手は複前層と同一視できる、ということです。ファミリー値反変関手 $`T`$ に対応する複前層を $`(\cat{C} \mid P_1, P_2)`$ とします。この(長さ 2 の)複前層を定義しましょう。
$`\cat{C}`$ は、反変関手 $`T`$ の域圏〈ソース圏〉です。これから長さ 0 の複前層 $`(\cat{C}\mid)`$ は自明に定義できます。定義より、$`\int (\cat{C}\mid) = \cat{C}`$ です。
次に、$`P_1 : (\int (\cat{C}\mid))^\op \to {\bf Set}`$ を定義します。以下のように定義します。
$`\quad \xymatrix{
{\cat{C}^\op} \ar[r]^T \ar[dr]_{P_1}
& {\bf Fam} \ar[d]^{\mrm{Dom}}
\\
{}
&{\bf Set}
}\\
\quad \text{commutative }\In {\bf CAT}\\
\text{i.e.}\\
\quad P_1 := T*\mrm{Dom} \In {\bf CAT}
`$
$`P_1`$ は $`\int (\cat{C}\mid)`$ からの集合値反変関手、つまり前層になるので $`(\cat{C} \mid P_1)`$ は長さ 1 の複前層になります。
$`P_2`$ は、複前層の定義から次の形の前層でなくてはなりません。
$`\quad P_2 : (\int(\cat{C} \mid P_1) )^\op \to {\bf Set} \In {\bf CAT}\\
\text{i.e.}\\
\quad P_2 \in |\mrm{PSh}(\int(\cat{C} \mid P_1) )|
`$
$`P_2`$ を定義するために、ファミリー値反変関手 $`T`$ の値を次の形に書きます*1。
$`\text{For }X \in |\cat{C}|\\
\quad T(X) = (\base{T(X)}, T_X^\to)\\
\text{Where}\\
\quad \base{T(X)} := \mrm{Dom}(T(X)) \in |{\bf Set}|\\
\quad T_X^\to : \base{T(X)} \to |{\bf Set}| \In {\bf SET}\\
\:\\
\text{For }f:X \to Y \In \cat{C}\\
\quad T(f:X\to Y) = (\base{T(f)}, T(f)^\flat )\\
\text{Where}\\
\quad \base{T(f)} := \mrm{Dom}(T(f)): \base{T(Y)} \to \base{T(X)} \In {\bf Set}\\
\quad T(f)^\flat : T_Y^\to \to \base{T(f)}^*(T_X^\to) \In {\bf Fam}[Y]
`$
ここで使った $`\base{\hyp}, (\hyp)^\flat`$ は、「Diag構成の変種とその書き方」で導入した記法で、ベースパート/ファイバーパートの概念がある射 $`\Phi`$ に関して $`\base{\Phi}, \Phi^\flat`$ として使う約束です。$`\base{\Phi}^*`$ は、ベースパートによる“引き戻し”です。ファミリーの準同型射 $`T(f)`$ にはベースパート/ファイバーパートの概念があります。また、ファミリー $`T(X)`$ のベースパートはその域〈インデキシング集合 | ベース集合〉だとしています。
$`\base{T(\hyp)} = P_1(\hyp)`$ となっていることに注意してください。
$`\quad \base{T(X)} = \mrm{Dom}(T(X)) = P_1(X)\\
\quad \base{T(f)} = \mrm{Dom}(T(f)) = P_1(f)
`$
さて、$`P_2`$ を定義しましょう。先に、全体の状況をポンチ絵にまとめておくと次のようです。
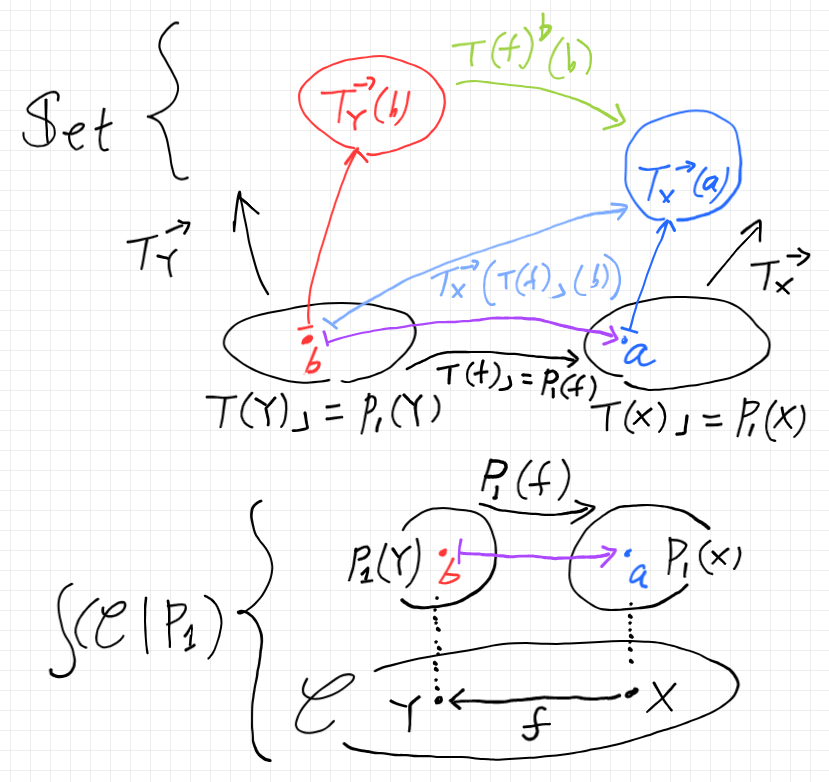
$`P_2`$ は圏 $`\int(\cat{C} \mid P_1)`$ の上の前層(集合値反変関手)ですから、$`\int(\cat{C} \mid P_1)`$ の対象と射に対する値を定義すればいいわけです。
- $`\int(\cat{C} \mid P_1)`$ の対象は、$`(X \in |\cat{C}|, a\in P_1(X))`$ という依存ペアである。
- $`\int(\cat{C} \mid P_1)`$ の射 $`f:(X, a) \to (B, b)`$ は、$`\cat{C}`$ の射 $`f:X \to Y`$ で、$`P_1(f)(b) = a`$ を満たすものである。(反変になっていることに注意。)
ファミリー値反変関手 $`T`$ を使って、$`P_2`$ を次のように定義します。
$`\text{For }(X, a) \in |\int(\cat{C} \mid P_1)|\\
\quad P_2(X, a) \in |{\bf Set}|\\
\qquad P_2(X, a) := T_X^\to (a) \; \in |{\bf Set}|\\
\:\\
\text{For }f: (X, a) \to (Y, b) \In \int(\cat{C} \mid P_1)\\
\quad P_2(f) : P_2(Y, b) \to P_2(X, a) \In {\bf Set}\\
\qquad P_2(f) := \big(\, T(f)^\flat(b) : T_Y^\to(b) \to T_X^\to(\base{T(f)}(b)) \In {\bf Set}\,\big)\\
\qquad\quad = \big(\, T(f)^\flat(b) : P_2(Y, b) \to P_2(X, P_1(f)(b)) \In {\bf Set}\,\big)\\
\qquad\quad = \big(\, T(f)^\flat(b) : P_2(Y, b) \to P_2(X, a) \In {\bf Set}\,\big)
`$
この定義により、$`P_2`$ が圏 $`\int(\cat{C} \mid P_1)`$ 上の反変関手になっていること(反変関手性)を確認する必要があります。面倒ですがルーチンワークです。また、先に 圏 $`\int(\cat{C} \mid P_1)`$ 上の集合値反変関手(前層)が与えられて、そこからファミリー値反変関手を構成することもできます。相互に逆な構成になっていることも、ルーチンワークをこなせば示すことができます。
おわりに
ファミリー値反変関手と長さ 2 の複前層の対応は、具体的な表示と計算によって示しましたが、もっと抽象的・一般的な定式化が出来そうな気がします。ファミリー値反変関手-複前層の対応は何らかのプルバック図式で与えられるとカッコイイのですが、どうもハッキリしません。
型理論的圏の一種であるファミリー付き圏〈CwF〉の定義が、複前層の圏のなかで遂行できるということは、またしてもスノーグローブ現象(「依存アクテゴリーに向けて // スノーグローブ現象/マイクロコスモ原理」「マイクロコスモ原理と逆帰納ステップ」参照)に出会っている気がします。スノーグローブ現象を積極的に利用した応用や手法があるのかも知れません。
*1:単なるイコールで書いていますが、右辺の書き方を左辺で規定しているので '$`=:`$' を使うのが適切かも知れません。