項・式など(と呼ばれる記号的存在物)の生成や操作に関連してモナドが現れることがあります。この種のモナドについて述べておきます。「構文論 vs. 意味論」という文脈で、構文機構の扱いやすい定式化が必要になりますからね。$`\newcommand{\cat}[1]{\mathcal{#1}}
\newcommand{\mrm}[1]{\mathrm{#1}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\In}{\text{ in }}
\newcommand{\Imp}{\Rightarrow}
\newcommand{\hyp}{ \text{-} }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\BR}[1]{ \left[\!\left[ {#1} \right]\!\right] }
`$
内容:
事例: 算術式のモナド
自然数定数(記号としての '0', '1', '2', ...)と足し算記号 '+' と掛け算記号 '*' と変数文字 'x', 'y', 'z' と丸括弧 '(', ')' から構成される算術式を考えます。例えば:
- 3
- 2 + 3
- x
- x + 1
- x + (3*x)
- x + y
- (x*x) + (y*y)
- x*(y + z)
足し算より掛け算を優先するという普通のルールを採用して、x + (3*x) は x + 3*x でもよいとします。その他、常識的な略記は認めます。
今述べたルールで作られるすべての算術式の集合を $`\mrm{ArithExp}(\{x, y, z\})`$ とします。変数の集合は変更可能で、's', 't' を変数に使った算術式の集合なら $`\mrm{ArithExp}(\{s, t\})`$ 、変数をまったく含まない算術式の集合なら $`\mrm{ArithExp}(\{\})`$ です。
このテの話をするとき困るのが、話題にしている構文的対象物と地の文のなかで使う記号の区別が難しいことです。フォントを変える方法もありますが、基本的には同じ書き方をします(文脈で判断)。どうしても区別したいときは、構文的対象物である算術式はバッククォートで囲むことにします。例えば、`x + 1` (LaTeX なら $``x + 1``$)のように。個々の文字・記号は、必要があればシングルクォートで囲みます(囲まないことが多いけど)。
変数の集合 $`\{x,y,z \}`$ から $`\{s, t\}`$ への次のような写像があったとします。
$`\quad f: \{x,y,z \} \to\{s, t\}\\
\qquad x \mapsto f(x) = s\\
\qquad y \mapsto f(y) = t\\
\qquad z \mapsto f(z) = t`$
この写像 $`f`$ から、
$`\quad \mrm{ArithExp}(\{x,y,z \}) \to \mrm{ArithExp}(\{s, t\}) \In {\bf Set}`$
が誘導されます。例えば(バッククォート使ってみます):
- `3` $`\:\mapsto`$ `3`
- `2 + 3` $`\:\mapsto`$ `2 + 3`
- `x` $`\:\mapsto`$ `s`
- `x + 1` $`\:\mapsto`$ `s + 1`
- `x + 3*x` $`\:\mapsto`$ `s + 3*s`
- `x + y` $`\:\mapsto`$ `s + t`
- `x*x + y*y` $`\:\mapsto`$ `s*s + t*t`
- `x*(y + z)` $`\:\mapsto`$ `s*(t + t)`
「変数とは何ぞや」とかどうでもいい事を考えるのをやめれば(任意の集合の任意の要素が変数であり定数でもある)、任意の集合(無限集合でもよい) $`X\in |{\bf Set}|`$ に対して $`\mrm{ArithExp}(X)`$ が定義できて、任意の写像 $`f: X \to Y \In {\bf Set}`$ に対して
$`\quad \mrm{ArithExp}(f) : \mrm{ArithExp}(X) \to \mrm{ArithExp}(Y) \In {\bf Set}`$
も定義できて、
$`\text{For }f: X \to Y, g:Y \to Z \In {\bf Set}\\
\quad \mrm{ArithExp}(f; g) = \mrm{ArithExp}(f) ; \mrm{ArithExp}(g)\In {\bf Set}\\
\text{For } X \in |{\bf Set}|\\
\quad \mrm{ArithExp}(\id_X) = \id_{\mrm{ArithExp}(X)}\In {\bf Set}
`$
が成立するので、$`\mrm{ArithExp}`$ は集合圏の自己関手 $`{\bf Set} \to {\bf Set} \In {\bf CAT}`$ となります。
入れ子の算術式の“平坦化”(展開計算ではない)により、次の写像が定義できます。これは、``x + 1` + 3*`x + 1`` $`\mapsto`$ `(x + 1) + 3*(x + 1)` とかです(下の補足参照)。
$`\quad \mu_X : \mrm{ArithExp}(\mrm{ArithExp}(X) ) \to \mrm{ArithExp}(X) \In {\bf Set}`$
単なる変数も算術式なので、次の写像も定義できます。これは、'x' $`\mapsto`$ `x` とかです。
$`\quad \eta_X : X \to \mrm{ArithExp}(X) \In {\bf Set}`$
写像の族 $`(\mu_X )_{X \in |{\bf Set}|},\, (\eta_X )_{X \in |{\bf Set}|}`$ は自然性(とある四角形図式の可換性)を満たすので自然変換になります。
以下で三種類の“恒等”を区別するので注意しておくと:
- $`\id_X`$ : 圏(今は集合圏)のなかの、対象 $`X`$ の恒等射 $`X\to X \In {\bf Set}`$
- $`\mrm{Id}_{\bf Set}`$ : 圏(今は集合圏)の恒等関手 $`{\bf Set}\to{\bf Set} \In {\bf CAT}`$
- $`\mrm{ID}_F`$ : (今は集合圏の)自己関手 $`F`$ の恒等自然変換 $`F \to F \In {\bf CAT}({\bf Set}, {\bf Set})`$
話を戻して、$`(\mrm{ArithExp}, \mu, \eta)`$ は以下の図式の可換性として表現される法則を満たすのでモナドになっています。アスタリスクは関手の結合と関手と自然変換のヒゲ結合〈whiskering〉を表す図式順記号です(「関手と自然変換の計算に出てくる演算子記号とか // 今後使う予定の演算子記号」参照)。
モナドの結合律:
$`\require{AMScd}
\begin{CD}
\mrm{ArithExp} *\mrm{ArithExp} *\mrm{ArithExp} @>{\mu * \mrm{ID}_\mrm{ArithExp} }>> \mrm{ArithExp} * \mrm{ArithExp} \\
@V{\mrm{ID}_\mrm{ArithExp} * \mu }VV @VV{\mu}V \\
\mrm{ArithExp} *\mrm{ArithExp} @>{\mu}>> \mrm{ArithExp}
\end{CD}\\
\text{commutative in }{\bf CAT}({\bf Set}, {\bf Set}) \text{ as a monoidal category}
`$
モナドの左単位律:
$`\begin{CD}
\mrm{Id}_{\bf Set} * \mrm{ArithExp} @>{\eta * \mrm{ID}_\mrm{ArithExp} }>> \mrm{ArithExp}*\mrm{ArithExp} \\
@| @VV{\mu}V\\
\mrm{ArithExp} @= \mrm{ArithExp}
\end{CD}\\
\text{commutative in }{\bf CAT}({\bf Set}, {\bf Set}) \text{ as a monoidal category}
`$
モナドの右単位律:
$`\begin{CD}
\mrm{ArithExp} * \mrm{Id}_{\bf Set} @>{\mrm{ID}_\mrm{ArithExp} * \eta }>> \mrm{ArithExp}*\mrm{ArithExp} \\
@| @VV{\mu}V\\
\mrm{ArithExp} @= \mrm{ArithExp}
\end{CD}\\
\text{commutative in }{\bf CAT}({\bf Set}, {\bf Set}) \text{ as a monoidal category}
`$
算術式のモナド $`\mrm{ArithExp}`$ は、基本的かつ簡単な構文的モナドの例です。
うーむ、やっぱり構文的対象物〈syntactic object〉の説明は難しいな。下の補足も読んでください。
文字・記号と算術式の区別や、入れ子の算術式の表記のために、シングルクォートやらバッククォートやらを使ったのですが、こういうテキスト表現ではやはり無理があります。算術式は、ノードに自然数〈を表す記号〉や演算子記号がくっついたツリーとみなしてください。
リーフ〈末端のノード〉には自然数がラベルされているか、なんかの集合 $`X`$ の要素がラベルされているかです。集合 $`X`$ の要素を便宜上(言葉のあやで)「変数」と呼んでますが、「集合 $`X`$ の要素」の同義語として「変数」を使っているだけです。
リーフをラベルするための集合 $`X`$ は任意なので、集合 $`X`$ が算術式の集合であってもかまいません。そのときは、入れ子の算術式となります。入れ子の算術式を平坦化するとは、入れ子の境界を消し去って、単一の算術式だと思うことです。そのことを、
``x + 1` + 3*`x + 1`` $`\mapsto`$ `(x + 1) + 3*(x + 1)`
のような苦し紛れのテキスト表現で書いていました。
``x + 1` + 3*`x + 1`` をツリーの絵で描くなら次のようです。
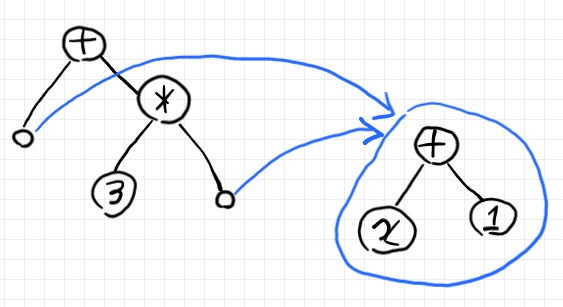
`・ + 3*・` のようなツリーの末端である黒丸(・)のラベルとして別なツリー `x + 1` が割り当てられています。水色がラベル割り当てを表しています。
末端に割り当てられているラベルをツリーに組み込んでしまえば `(x + 1) + 3*(x + 1)` となります。それを絵に描くと:
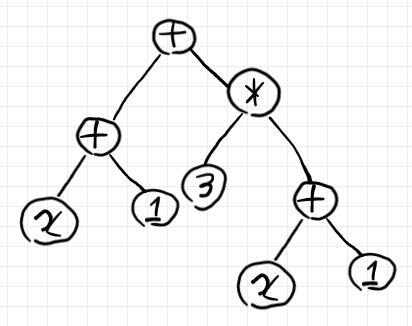
「項・式の変数」という言葉は、「ツリーのリーフ」や「ツリーのリーフに割り当てられているラベル」の意味で、ほんとに“言葉のあや”(ありていに言って誤用)として使っています。
[/補足]
包含関係に対する単調性
前節で算術式のモナドの例を挙げました。他にも構文的なモナドの例はありますが、“構文的モナド”という概念をある程度公理化しましょう。「ある程度」というのは、公理系を出発点とする議論を展開するわけではなくて、算術式のモナドのような実例の性質をまとめておこう、という程度だからです。
さて、算術式のモナドのような構文的モナドの特徴ですぐ気がつくのは、集合の包含関係に対して単調なことです。単調性は、モナドの台関手の性質です。一般に、集合圏の自己関手 $`F:{\bf Set}\to {\bf Set}`$ が包含関係に対して単調とは:
$`\text{For } X, Y\in |{\bf Set}|\\
\quad X\subseteq Y \Imp F(X)\subseteq F(Y)`$
一般の圏 $`\cat{C}`$ の自己関手 $`F:\cat{C}\to \cat{C}`$ に対して、このような単調性は定義できません。しかし、「圏の束構造と包含的圏」で述べたような公理的包含関係を持つ圏なら、その公理的包含関係に対する単調性を定義できます。
集合圏では、空集合は始対象であると同時に、包含順序に関する最小限です。したがって、次が成立します。
$`\text{For } X \in |{\bf Set}|\\
\quad F(\emptyset) \subseteq F(X)`$
$`F(\emptyset)`$ は“閉じた項の集合”に対応するもので重要です。$`\mrm{ArithExp}(\emptyset)`$ は、自然数(を表す記号)と演算子記号と丸括弧を組み合わせた項の集合です。
変数集合
構文モナドにおける $`F(X)`$ は項の集合です。$`F(X)`$ の要素が項です。項に対して、「項に出現する変数の集合」を定義できます。$`t\in F(X)`$ の変数の集合を $`\psi(t)`$ とします。すると、$`\psi(t) \in \mrm{Pow}(X)`$ です。$`\psi`$ は 関手 $`F`$ と共変ベキ集合関手 $`\mrm{Pow}`$ を結ぶ自然変換となります。
$`\quad \psi :: F \twoto \mrm{Pow} : {\bf Set} \to {\bf Set} \In {\bf CAT}`$
自然変換の成分と自然性の可換図式は以下のようになります。
$`\text{For } X \in |{\bf Set}|\\
\quad \psi_X : F(X) \to \mrm{Pow}(X)\\
\:\\
\text{For } f:X\to Y \in |{\bf Set}|\\
\begin{CD}
F(X) @>{\psi_X}>> \mrm{Pow}(X)\\
@V{F(f)}VV @VV{\mrm{Pow}(f)}V \\
F(Y) @>{\psi_Y}>> \mrm{Pow}(X)
\end{CD}\\
\text{commutative in }{\bf Set}`$
「項 $`t`$ の変数の集合」という言葉を使ってますが、繰り返しますが“言葉のあや”です。「ツリー $`t`$ のリーフ〈末端〉ノードに実際に割り当てられたラベルの集合」と解釈してください。
$`\psi(t) = \psi_X(t)`$ が変数の集合なら次が成立します。
$`\text{For }t \in F(X)\\
\quad t \in F(\psi_X(t))`$
変数集合 $`\psi(t)`$ は、上記の性質を満たす集合のなかで最小のはずですから、次も言えます。
$`\text{For }t \in F(X)\\
\quad \forall Y\in \mrm{Pow}(X). t \in F(Y) \Imp \psi_X(t) \subseteq Y`$
これが、$`\psi(t)`$ の特徴付けです。
クライスリ射の作用と変数リネーム
構文的モナド $`F = (F, \mu, \eta)`$ (記号の乱用)はモナドなので、そのクライスリ圏を定義できます。モナドのクライスリ圏は $`\mrm{Kl}(F/{\bf Set})`$ と書くことにします。モナドの基礎圏 $`{\bf Set}`$ が周知なら省略して、クライスリ圏を $`\mrm{Kl}(F)`$ とも書きます。
実際には、クライスリ圏 $`\mrm{Kl}(F)`$ よりも、その反対圏 $`\mrm{Kl}(F)^\mrm{op}`$ を使っていることが多い気がしますが、射の向きで混乱する恐れがあるので、ここではクライスリ圏だけを考えます。
もとの圏(今は集合圏)とそのクライスリ圏における結合〈composition〉の記号は次のように約束します。
| 図式順 | 反図式順 | |
| もとの圏の結合 | $`;`$ | $`\circ`$ |
| クライスリ圏の結合 | $`;;`$ | $`\odot`$ |
また、クライスリ圏の恒等射を $`\mrm{kid}_X`$ とします。クライスリ拡張を $`(\hyp)^\#`$ で表すことにすると、クライスリ圏の結合と恒等射は次のように書けます。
$`\text{For }f:X \to F(Y), g:Y \to F(Z) \In {\bf Set}\\
\quad f ;; g = g \odot f := f ; g^\# = g^\# \circ f\\
\text{For} X \in |{\bf Set}|\\
\quad \mrm{kid}_X := \eta_X
`$
項($`F(X)`$ の要素)に対するクライスリ射(クライスリ圏の射)の“作用”は次のように定義します。
$`\text{For } f: X \to Y \In \mrm{Kl}(F)\\
\text{For } t \in F(X)\\
\quad t^f := f^\# (t) \: \in F(Y)`$
クライスリ圏の射の向き(反対圏ではない)を採用すると、項はクライスリ射で前送りされます。次の前送り公式が成立します。
$`\text{For } f: X \to Y, g:Y \to Z \In \mrm{Kl}(F)\\
\text{For } t \in F(X)\\
\quad (t^f)^g = t^{f;;g}`$
反図式順の結合記号で書けば次のようです。
$`\quad (t^f)^g = t^{g \odot f}`$
この場合は、クライスリ射を左肩に乗せるほうが自然に見えます。
$`\quad {^g({^ft})} = {^{g \odot f}t}`$
$`h : X \to Y \In {\bf Set}`$ が集合圏で可逆な写像とします。そのとき、$`h' := h; \eta_Y`$ はクライスリ圏でも可逆になります。$`t\in F(X)`$ に対する $`t^{h'}`$ は、項に出現する変数を $`h`$ でリネームした項と考えることができます。「リネーム」も、もちろん“言葉のあや”です。なお、$`h`$ と $`h'`$ は同一視する($`{\bf Set}\subseteq \mrm{Kl}(F)`$ と考える)こともあります。
$`t\in F(X), s\in F(Y)`$ が、可逆な $`h:X \to Y`$ により $`s = t^{h'}`$ と書けるとき、$`t`$ と $`s`$ はアルファ同値(リネームで移りあえる)だと言えます。
項の値を計算する
算術式の場合 $`\mrm{ArithExp}(\emptyset)`$ は変数を含まない式、例えば 1 + 2 や 3 + 5*3 など(バッククォートで囲んでないけど)です。これらの式は“常識的に計算”できます。
- `1 + 2` $`\mapsto`$ 3
- `3 + 5*3` $`\mapsto`$ 18
$`\mapsto`$ の左側は $`\mrm{ArithExe}(\emptyset)`$ の要素で、右側は $`{\bf N}`$ の要素と考えます。
“常識的な計算”のような、閉じた項に値を対応させる写像を次のように書きます。
$`\quad d: F(\emptyset) \to V \In {\bf Set}`$
ここで、$`V`$ は値の集合です。値は項とみなせるので、次の写像も要求します。
$`\quad l:V \to F(\emptyset) \In {\bf Set}`$
項としての値の計算結果は、その値そのものですから、次は成立します。
$`\quad l;d = \id_V : V\to V \In {\bf Set}`$
$`F(\emptyset)`$ を $`X`$ と置いて一般化した4つ組 $`(X, V, d, l)`$ を還元系〈reduction system〉と呼ぶことにします*1。自然数の常識的な計算以外に、ラムダ計算のデルタ還元〈delta reduction | デルタ変換 | delta conversion〉からも還元系を作れます。
還元系 $`(X, V, d, l)`$ があるとき、$`c := d;l`$ と定義すると、
- $`c:X \to X \In {\bf Set}`$
- $`c;c = c : X \to X \In {\bf Set}`$
が成立します。逆に、上のような $`(X, c)`$ があると、次のように定義して還元系 $`(X, V, d, l)`$ を作れます。
- $`V := \mrm{Img}(c)`$ (写像 $`c`$ の像集合)
- $`d := c|^V`$ (写像 $`c`$ の余域を $`V \subseteq X`$ に制限した写像)
- $`l := \mrm{incl}_V^X`$ ($`V \subseteq X`$ の包含写像〈inclusion map〉)
以下、還元系 $`(F(\emptyset), V, d, l)`$ を固定して、記号の乱用で $`V = (F(\emptyset), V, d, l)`$ と略記します。つまり、(ややイレギュラーかも知れませんが)還元系 $`V`$ と呼びます。
$`v : X \to F(\emptyset)`$ を、集合 $`X`$ 上の付値〈valuation | value assignment〉と呼びます。付値は、集合 $`X`$ を変数の集合と思ったときに、変数の具体化になります。ただし何度も言うように、「変数」も「具体化」も“言葉のあや”です。
付値 $`v`$ をクライスリ射(クライスリ圏の射)とみると、空集合への射になります。
$`\quad v:X \to \emptyset \In \mrm{Kl}(F)`$
$`X`$ 上の付値 $`v`$ があると、還元系 $`V`$ を使って項の値を計算できます。項の値をスコットブラケット $`\BR{\hyp}`$ を使って表すと、その定義は次のようになります。
$`\text{For } t\in F(X)\\
\quad \BR{t}^V_v := (v^\#; d)(t)`$
ここで、$`(\hyp)^\#`$ はモナド $`F`$ に伴うクライスリ拡張で、$`d`$ は還元系 $`V`$ の還元写像(計算を実行する写像)です。
次のように変形できます。
$`\quad \BR{t}^V_v \\
:= (v^\#; d)(t)\\
= (d \circ v^\#)(t)\\
= d( v^\# (t) )\\
= d(t^v)`$
$`X`$ 上の項 $`t`$ を、付値 $`v`$ で $`\emptyset`$ 上まで前送りした結果 $`t^v \in F(\emptyset)`$ を還元写像 $`d`$ で計算して値を得ます。
$`X`$ 上の付値の全体を $`\mrm{Val}(X)`$ としましょう。
$`\quad \mrm{Val}(X) := \mrm{Kl}(F)(X, \emptyset) = {\bf Set}(X, F(\emptyset))`$
すると、一種の評価写像を次のように定義できます。
$`\text{For} X \in |{\bf Set}|\\
\quad \mrm{ev}_X : F(X)\times \mrm{Val}(X) \to V\\
\text{Where}\\
\quad \mrm{ev}_X(t, v) := \BR{t}^V_v`$
変数を含む(かも知れない)式 $`t`$ を変数の値割り当て環境 $`v`$ のもとで評価することなので、$`\mrm{ev}_X`$ は“評価”の直感にフィットしています。
以上ザッと見たように、構文的な対象物や操作をモナドを使って定式化すると、比較的見通しが良い描像が得られます。
*1:還元系は、集合圏におけるEPペア〈embedding-projection pair〉です。