絵を描いて学ぶ・プログラマのためのラムダ計算

「JavaScriptで学ぶ・プログラマのためのラムダ計算」は、1回では述べ切らなくて、一段落付いたところで区切りました。これはかえって良かったですね、ブックマークやトラックバックでフィードバックが得られたので。

そのフィードバックなどをかんがみて、「残り＝次回の話題」として予告した内容とは食い違ってしまうのだけど、今回は、文章では伝わりにくい（前回うまく伝わらなかったと思える）ラムダ計算の大事なツボを、なんとか表現してみようと思います。

［このエントリーの内容はだいぶ前にほぼ出来上がっていたのだけど、ココに書いてある事情で、“お絵描き”がなかなか出来なかったのです。］

※印刷のときはサイドバーが消えます。
内容：

知っていて損はない

僕が「ラムダ計算は知っておいたほうがいい」と思う理由は、形式的計算体系としての“純粋ラムダ計算”が理論的に重要だから、というだけではありません。むしろ、次に述べるようなことがより大きな動機となります。

まず、関数を表現する方法としてのラムダ記法（lambda notation）に慣れて、紙と鉛筆によるインフォーマルなラムダ計算が出来ると、けっこうそれを使える場面が多いのです。例えば、「JavaScriptによるテンプレート・モナド、すっげー簡単!」の最後で、モナド法則を示すために、インフォーマルなラムダ計算を使っています。

ある種の計算的実体（例：クロージャ）や計算手法（例：継続ベースの計算）の説明にもラムダ式がよく使われます。式言語（EL; expression language）に対する処理系（パーザーやエバリュエータ）を作る場合なども、ラムダ計算が良いヒントになるでしょう。もちろんラムダ計算は、既存の関数型言語を理解する基盤となります。あるいは、新しいプログラミング言語を設計する際にもラムダ計算が規範になるかも知れません。

計算は身体的に理解しよう

少し説教じみたことを言います； ラムダ計算に限らず、“計算”は機械にやらせる前に、まず自分自身の身体的行為として実行できるようにしましょう。要するに、紙と鉛筆を使い、自分の目と手を動かして、肉体的運動としての計算を遂行してみましょう、ってことです。

僕は根性主義は大嫌いですが、身体的理解は強調します。コンピュータに計算を実行させる（プログラムにより実装する）場合でも、それは、自分自身の動作／作業をコンピュータに代わりにやらせることですから、前もって自分の体を使った計算が出来る必要がありますよね。（まー、実装しながら分かることも多いですが。）

ところで、紙と鉛筆による計算というと、一次元的に並んだ記号列の変形操作と思うでしょうが（実際、そういうことも多いですが）、むしろ、ある種の図形を描きかえていくと思ったほうが自然なこともあります。ラムダ計算も、図形を描き換える操作と捉＜とら＞えると、ずっと直感（直観）にうったえ、より身体的な理解が得られると思います。

というわけで、「ホワイトボードがあれば、こんな絵を描いて説明するだろう」という絵をまじえて、ラムダ式とβ変換を視覚的・図形的に了解する方法を説明します。この図形的方法には次のメリットがあります。

1. 直感的、身体的にラムダ計算を理解できる。
2. 紙と鉛筆によるラムダ計算をするときに、実際的な助けとなる。
3. プログラムにより“計算”を実装するとき、記号列の変形よりもずっと役に立つ（実装方式に直接的なヒントを与える）。
4. Lisp系言語の内部的データ構造として、なぜ二進木が使われているか納得できる。

ラムダ項のツリー表示：準備

「JavaScriptで学ぶ・プログラマのためのラムダ計算」で次のように言いました。

先頭がλではじまる式は、もちろんラムダ式と呼びますが、これは狭い意味のラムダ式です。定数／変数／組み込み演算子／組み込み関数など（を表す記号）を、何度か（0回でもよい）の適用操作により組み立てた表現もまたラムダ式と呼ぶことがあります -- こっちは広い意味のラムダ式、ラムダ計算体系内の表現のことです。

以下では、話がこんがらからないように、ラムダ式と言えば“狭い意味のラムダ式”だとして、“広い意味のラムダ式”はラムダ項（lambda term）、あるいは単に項（term）と呼ぶことにします（この区別が一般的なわけではありません）。

さて、ラムダ項をツリーで視覚的に表示するのですが、ツリーの末端（リーフ）は次の3種のどれかです。

1. 変数：x, y, fooなど。
2. 定数（整数や文字列などを直接表すデータ・リテラル）：1, 3.14, "hello"など。
3. 組み込み演算子、組み込み関数：足し算+, 掛け算*, 平方根sqrtなど。

末端以外のノードは次の2種です。

1. 適用ノード
2. タプリング・ノード

説明をする前に、実例を出してしまいましょう。(x + 1)*y という算数の式（これもラムダ項のひとつです）は、次のツリーになります。

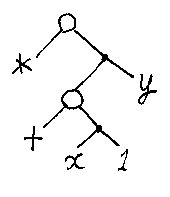
白丸が適用ノード、枝分かれ（小さな黒丸）がタプリング・ノードです -- 次節でこれらのノードについて詳しく説明します。

ラムダ項のツリー表示：描く！

まず、適用ノードの説明； 関数fに引数xを渡した形、つまり適用した形 f(x) をツリーで図示するときは、白丸の適用ノードを描いて、左下にf、右下にxをぶら下げます。

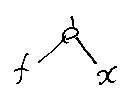
f(x, y)のようなときは、適用ノード（白丸）から枝を3本出す方法もありますが、ここではタプリング・ノードを使うことにします（ここらへんの選択は趣味の問題に過ぎませんが）。タプリング（tupling）は、タプル（tuple）を作ること、そしてタプルとは複数のモノを並べた組＜くみ＞のことです。組化＜くみか＞という日本語もあるようですが、カタカナ語にしておきます。

xとyのタプルは(x, y)と書くのが普通です。が、丸括弧があまりに多用されているので、<x, y>を使う人もいます。引数が2つある f(x, y) を、タプル引数が１つの f(<x, y>)と見なすわけです。この、xとyからタプル<x, y>を作る操作がタプリングで、ツリーの図では枝分かれノードで示します。

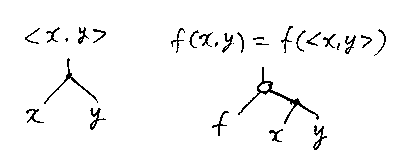
足し算'+'や掛け算'*'のような演算子も図示のときは関数だとみなします。つまり、x + y は、+(x, y) のように、2引数関数+への適用として扱います。

残るはラムダ式（記号λではじめる式）です。Eがなにかのラムダ項だとして、λx.E は、E（に対応する図形）を四角の箱に入れて示します。例えば、λx.[(x + 1)*y]なら次のようです。（丸括弧以外に角括弧も使いますが、特に違いはありません。）

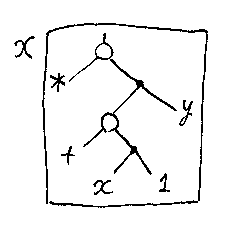
λの直後にある引数変数は、箱の左側に添えておくことにします。こうしてできたラムダ式（関数表現）に対応する箱をラムダ箱と呼ぶことにします。

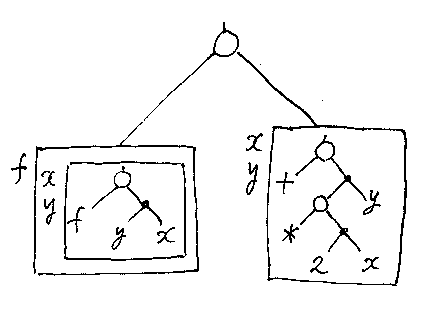
慣れてくれば、複雑なラムダ項、例えば、(λf.λ(x, y).f(y, x))(λ(x, y).(2*x + y)) を図示することもできるようになります。ラムダ箱を使った図は次のよう。(λf.λ(x, y).f(y, x))(λ(x, y).(2*x + y)) の意味がわからなくても図には描けますね。

練習問題 1： 次のラムダ項を図に描いてください。

1. 1 + 2
2. x*x
3. 2*x + 1
4. f(f(x))
5. λx.x
6. λx.(2*x + 1)
7. λ(x, y).(x + y)
8. λx.f(f(x))
9. z + (λ(x, y).(x + y))(2, 3)
10. (λx.(2*x + 1))[(λx.(x*x))(4)]

β変換に対応するツリーの描き換え

ラムダ計算における“計算”とはβ変換のことです。そして、β変換はまったく機械的な操作なのです。このβ変換をツリーの描き換えとして説明しましょう。

雰囲気としては、β変換とは次のような操作です。

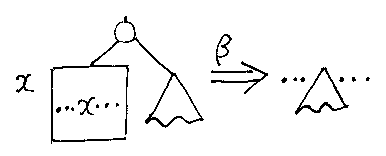
β変換を行うには、最初に変換可能な部分を探します。変換可能な部分とは：

• 適用ノードの左側がラムダ箱になっているところ

です。β変換可能な適用ノードを見つけたら、次の手順を実行します。

1. ラムダ箱の中身を箱から取り出します。（箱は捨てます。）
2. その中身に出現する変数（ツリーの末端にある）を、適用ノードの右側にぶら下がっている引数（に対応する図形）で置き換えていきます。変数を繋ぎ目として接ぎ木する感じです。
3. 引数変数名と、適用ノードの右にぶら下がっている実際の引数との対応関係は、ラムダ箱の左端に添えられている引数変数（の並び）を見ながら判断します。
4. 置き換えが済んだ図形がβ変換の結果です。（もともとあった適用ノードも捨ててください。）

やってみましょう。(λ(x, y).(x + y))(2, 3) → 2 + 3 という変換です。

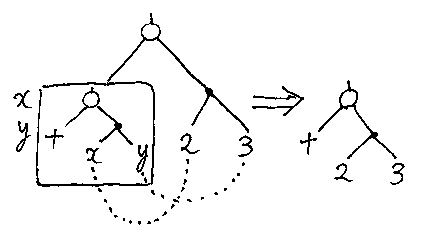
図のルート位置にあった適用ノード（白丸）は消えて、ラムダ箱の中に入っていた適用ノードが外に出ます。

練習問題 2： 次のラムダ項をβ変換してください。

1. (λx.x)(7)
2. (λx.(2*x + 1))(4)
3. (λx.f(f(x)))(4)
4. z + (λ(x, y).(x + y))(2, 3)

もっとβ変換をやってみよう

もっと練習しましょう。例題は (λx.x*x)[(λx.(x + 1))(4)] です。この場合、β変換可能な適用ノードが2箇所あります。以下の図は、ツリーのルートにある適用ノードから先にβ変換をした計算過程です。

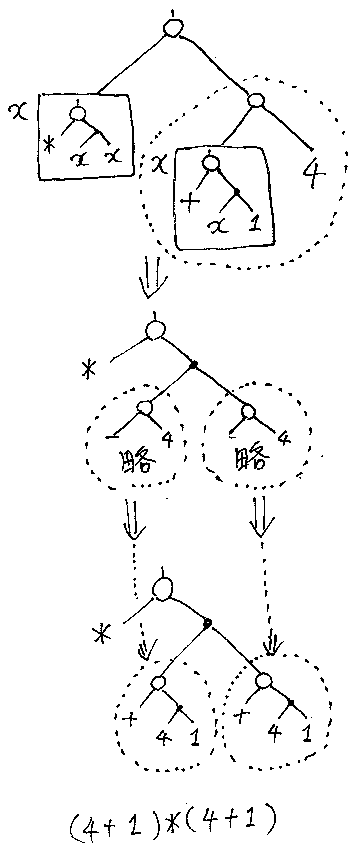
練習問題 3： 例とは異なる適用ノードからβ変換を行って計算（ツリー描き換え）をしてください。

練習問題 4： (λx.(2*x + 1))[(λx.x*x)(4)] を計算してください。最後に数の計算もしましょう。

次は少し難しいですよ。[(λf.λx.f(x, x))(λ(x, y).(x + y))](5) です。眺めて考え込んでいると、かえってワケワカラナクなるので、とにかく手を動かすことです。規則に忠実に従って絵を描き、規則に従ってβ変換を実行しましょう。とにかく機械的にやるのがコツです。最初は、式全体をツリーで描きます。

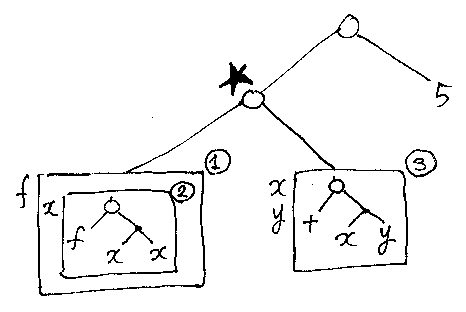
ルートと右下の5は忘れて、左にぶら下がっている部分（サブツリー）を先に片づけましょう。星印（★）の適用ノードをβ変換すれば、(1)のラムダ箱は消えるはずです。しかし、(2)のラムダ箱は残ります。なぜなら、1回のβ変換では「1個の適用ノードと1個のラムダ箱」しか消せないからです。とにかく規則に従えば、ラムダ箱(2)の内部にある変数f（このfは変数です！）を、ラムダ箱(3)で置き換えることになります。次のようになります。

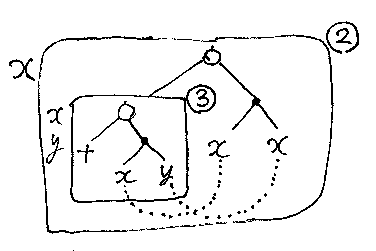
なんだかよくわからない人は、β変換の規則をもう一度読み直してください。fのところに、右にぶら下がっていた箱をそのまま置いたのです。

ついでですから、ラムダ箱(2)のなかをβ変換してしまいましょう。えっ、「ラムダ箱の中身を操作してもいいのか？」って。いいですよ。β変換はどこからやってもいいのです。

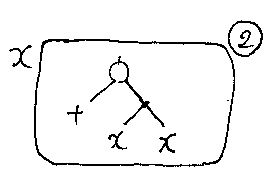
ラムダ箱(2)のなかにあったラムダ箱(3)が消えて、結果は、1個の入れ子なしラムダ箱です。これを、もとの大きなツリーの左側に置きましょう。

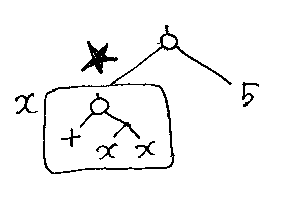
おっ、またβ変換ができますね。やってみてください。最後に数の計算（算数）をすれば1つの整数値が得られます。

練習問題 5： 例の結果である値（数値）はいくつですか。
練習問題 6： [(λf.λ(x, y).f(y, x))(λ(x, y).(2*x + y))](2, 3) を計算してください。最後に数の計算もしましょう。
練習問題 7： 今までに出てきたラムダ項、あるいは自分で作り出したラムダ項をさまざまに組み合わせて計算をしてみてください。

計算現象を体験するということ

どうでしょう、「計算を身体的に理解する」、「機械にやらせるべき操作を、紙と鉛筆で自ら実行してみる」とはどういうことか、感じが伝わりましたでしょうか？

僕はしばしば計算現象という言葉を使います。計算が進行していく状況（一種の運動です）、その運動を支配している法則などは、物理現象とそう大きくは違わないと思えるので、「現象」という言葉使いが気に入っているのです。

プラトニックに考えれば、ラムダ計算現象も実在すると思えます。ツリーを描き換えていく作業は、ラムダ計算現象を紙の上でシミュレートしている（いや、むしろ現象そのものが生起している）のです。