僕は長年のストリング図ユーザーでストリング図ファンです。「ストリング図は役に立つ」と断言できます。よって、ストリング図の使用を推奨したいし、推奨しています。では、ストリング図が“使える”とはどういうことでしょうか?
ストリング図、それと後で述べるストリング図動画が使えるようになるとは、ある種の作品を創作できるようになることです。絵画・イラストやアニメーションは作品ですが、ストリング図/ストリング図動画によりそういう作品が創れるようになるのです。自分で作品を創ることを目標に学ぶといいでしょう。
論理の文脈においては、作品は証明です。したがって、作品が創れるようになるとは、(形式的な)証明が書けるようになることです。関数型プログラミングの文脈では、作品はプログラムです。作品が創れるようになるとは、プログラムが書けるようになることです。
自分で作品を創るのではなくて、誰かが作品を創るための素材/道具を準備する作業もとても大事です。これは、公理系を設定することや仕様を記述する作業になります。
作品を創作すること/創作環境を構築すること、そういうスキル/能力を獲得することは、目標にするに値すると思いませんか。それに、作品を創作すること/創作環境を構築することって、楽しいし。
この記事では、作品創作の観点から、ストリング図にまつわる事項を幾つか述べます。普段見逃されがちな概念に注目することにします。$`
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\mbf}[1]{ \mathbf{#1} }
\newcommand{\mrm}[1]{ \mathrm{#1} }
\newcommand{\o}[1]{ \overline{#1} }
%\newcommand{\u}[1]{ \underline{#1} }
\newcommand{\id}{ \mathrm{id} }
\newcommand{\In}{ \text{ in }}
%\newcommand{\On}{ \text{ on }}
\newcommand{\Iff}{ \Leftrightarrow }
\newcommand{\Imp}{ \Rightarrow }
\newcommand{\op}{ \mathrm{op}}
\newcommand{\hyp}{\text{-} }
\newcommand{\twoto}{\Rightarrow }
\newcommand{\T}[1]{\text{#1} }
\require{color}
\newcommand{\NX}[1]{ \textcolor{orange}{ {#1}} } % New Expression
\newcommand{\KX}[1]{ \textcolor{blue}{#1} } % Known EXpression
`$
内容:
ストリング図動画
ストリング図〈string diagram〉は、2次元平面に描かれた絵図〈picture | figure | diagram〉です。実は、2次元描画では表現し切れないことは多くあります。より多次元の絵図が必要になります。3次元空間のなかに描かれた絵図はサーフェイス図〈surface diagram〉といいます。例えば以下は、過去記事「「コミュニケーションの多次元化」という革命に立ち会っているのだと思う」で引用したサイモン・ウィラートン (Simon Willerton) の論文 "A diagrammatic approach to Hopf monads" からのサーフェイス図です。

見れば分かるように、サーフェイス図を描くのは手間がかかる面倒な作業です。専用のソフトウェアも見当たらないので、Blender のような汎用ツールで頑張っているのが現状でしょう*1。
3次元空間への描画の代わりに、時間に沿って動く2次元絵図、つまり2Dアニメーションを使う方法があります。アニメーション動画〈animation movie〉は、原理としては紙芝居やパラパラ漫画と同じです。フレーム〈静止画のコマ〉をたくさん準備して高速に再現すればなめらかな(ヌルヌルした)アニメーションになります。何千枚ものフレームを準備するのは現実的ではないので、数枚程度の静止画〈still | スチル | 静画〉からなるパラパラ・カクカクな動画でもいいとします。極端なケースとしては、2枚の静止画でも動画〈movie | ムービー〉だとみなします。
以下は、過去記事「図式思考の例として、ラックス・モノイド関手について考えてみる」で引用したブルース・バートレット〈Bruce Bartlett〉の論文 "Quasistrict symmetric monoidal 2-categories via wire diagrams" からの絵です。
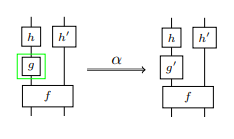
これは、before(左) と after(右) の2枚の静止画〈フレーム〉からなるアニメーション動画です。最も簡単な動画ですね。アニメーション動画の用語では、2枚の静止画〈フレーム〉のあいだの“移り変わり”を遷移〈transition | トランジション〉といいます。上の図の $`\alpha`$ は before(左) から after(右) への遷移です。
2次元ストリング図を静止画〈フレーム〉として、「静止画, 遷移, 静止画, 遷移, ‥‥, 静止画」という系列をストリング図動画〈string diagram movie〉と呼びましょう。ストリング図動画は、3次元空間に描かれたサーフェイス図の代替表現です。“空間3次元”を“空間2次元+時間”で代替しています。
では、4次元空間に描かれた3次元図形はどう表現したらいいでしょうか。“空間4次元”を目視するわけにはいかないので、“空間3次元+時間”で代替します。先に引用したウィラートンのサーフェイス図は、実は、サーフェイス図アニメーション動画の一枚のフレームでした。以下のような等式的変形として書かれていますが、順番に見ていけば、6枚のサーフェイス図のパラパラ漫画です。
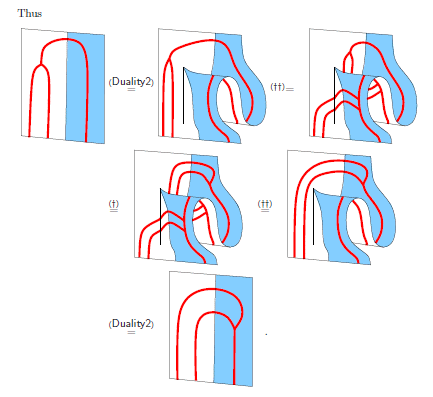
高次元結び目理論では、ムービー遷移〈movie {move | transition}〉という表現手法が使われます。以下は、マシュー・グラハム〈Matthew Graham〉の論文 "MARKED CS MOVIES" からの引用です。

昔の映画フィルム(今や、実物を見る機会はないでしょう*2)に似せて描いてあります。縦に3コマ(5コマも混じっている)が一本の映画フィルムです。番号が付いた特殊な矢印は、ムービー〈動画 | 映画〉のあいだの遷移〈move | transition〉です(この例では双方向遷移です)。全部で15種のムービー遷移が描かれています。
3コマ・フィルムのそれぞれのコマ(静止画)は2次元絵図のようですが、よく見ると奥行きを持っていて3次元絵図なのです*3。個々のコマが3次元絵図なので、ムービー(3コマ・フィルム)は4次元絵図を表します。ムービー遷移は時間方向を使ってますが、結局は5次元空間内の絵図の表現となります。高次元空間内に居る幾何的対象物をなんとか可視化しようとする工夫のひとつがムービー遷移です。
ストリング図動画は“空間2次元+時間”なので3次元までしか扱えませんが、多くの現象・事態が3次元までで表現可能です。ストリング図動画は、十分に強力な表現・計算デバイスです。
キャンバス
ストリング図はボックス&ワイヤー図〈boxes-and-wires diagram〉とも呼びます。ボックスとワイヤーが絵図の素子〈picture element〉です。絵を自由に描くというよりは、レゴブロックを組み立てるように、既存のガジェットを組み合わせて創作物〈作品〉を創り出します。
ストリング図を描く場所、絵図の素子(ボックスとワイヤー)を置く場所をキャンバス〈canvas〉と呼びます。キャンバスを意識しないことも多いようですが、キャンバスはそれ自体で幾何的物体〈geometric {material | object}〉であり、キャンバス操作の対象になります。キャンバスは常に意識すべきものです。
キャンバスにはキャンバス形状があります。大分類すると、円板形状のキャンバス〈{disk | disc}-shaped canvas〉と矩形形状のキャンバス〈rectangle-shaped canvas〉があります。注意すべきは、概念的・理論的な意味でのキャンバス形状と、実際に描く場合の具体的形状があることです。具体的形状は、描きやすさや見た目の好みがあるので、人により場合により変わっても問題ありません。ここで言っている円板形状キャンバスと矩形形状キャンバスは、概念的・理論的な分類です。概念的・理論的な矩形形状キャンバスを、具体的な描画では丸で描いても別にかまいません。
円板形状のキャンバスは、方向〈direction〉も向き〈orientation〉も持ちません。方向と向きは違う概念です。その違いを説明するのは面倒なので今はしません*4が、方向も向きもないとは「座標軸のようなものが定まってない」と理解してください。それに対して矩形キャンバスでは、通常のデカルト座標と同じ座表軸があります。ひとつの軸が定める方向を横方向、もうひとつの軸が定める方向は縦方向です。
方向も向きもないキャンバスというのは人間には考えにくいようです。僕の経験と観察では、方向と向きを持った矩形キャンバスに十分に慣れた後で、徐々に方向・向きを抜き去って円板キャンバスに至るという道筋を通らないと、円板キャンバスは理解困難なようです。
矩形キャンバスは最初から横方向・縦方向が備わっているので理解しやすいのですが、縦・横をどのように使うかは別に取り決めが必要です。その取り決め〈約束〉は残念ながら人により場合によりバラバラです。その事情は次の過去記事達(特に最初の記事)に書いています。
描画のためのツールバッグと指標
ストリング図は、キャンバスの上にボックスを配置して、ワイヤーで結ぶことで描き出します。絵の具と筆で描くような作業より、レゴブロックやピクチャーパズルを組み立てる作業に近いです。あるいは、回路素子と電線から電気回路〈electrical circuit〉を組み立てる作業に近いとも言えます。


ストリング図の描画(むしろ組み立て)に必要な素材・道具一式を(描画のための)ツールバッグ〈toolbag〉と呼ぶことにします。ツールバッグに入っている素材・道具には次のものがあります。
- 使えるワイヤー〈wire〉、あるいは使える(ワイヤーの)色〈color〉
- 使えるボックス〈box | ノード | node | セル | cell〉
ストリング図動画〈ムービー〉を作る場合はさらに、基本的な遷移〈トランジション〉が必要です。
- 使える図の変形〈diagram deformation〉
図の変形を組み合わせて、動画の遷移を構成します。
というわけで、ツールバッグには、目的に応じたワイヤー(の色)、ボックス、図の変形の一式が詰め合わされています。ツールバッグの内容をテキストで表現したものが指標〈signature〉です。例えば、可換モノイドの指標〈commutative monoid〉は次のようです*6。
$`\T{signature }\NX{\mrm{CommMonoid}}\: \{\\
\quad \T{sort }\NX{A}\\
\quad \T{operation }\NX{m}: A \KX{\times} A \to A\\
\quad \T{operation }\NX{e}: \KX{\mbf{1}} \to A\\
\quad \T{equation }\NX{\T{comm}} :: \KX{\sigma}_{A,A} \KX{;} m \twoto m : A \KX{\times} A \to A\\
\quad \T{equation }\NX{\T{assoc}} :: (m \KX{\times} \KX{\id}_A) \KX{;} m \twoto (\KX{\id}_A \KX{\times} m) \KX{;} m : A \KX{\times} A \KX{\times} A \to A\\
\quad \T{equation }\NX{\T{unit}} :: (\KX{\id}_A \KX{\times} e) \KX{;} m \twoto \KX{\id}_A : A \to A\\
\}
`$
文字色の約束は「構造記述のための指標と名前 1/n 基本」と同じで; オレンジ色は初出の名前、青色は既知の名前です。一回オレンジ色で導入した名前は、その後は黒で書いてます。
この指標の等式的法則〈equational law〉である $`\T{comm}, \T{assoc}, \T{unit}`$ (可換律、結合律、単位律)をストリング図の変形として描いたのが次の図です。これは、ボンチ達〈Filippo Bonchi, Fabio Gadducci, Aleks Kissinger, Pawel Sobocinski, Fabio Zanasi〉の論文 "Rewriting modulo symmetric monoidal structure" からの引用です。
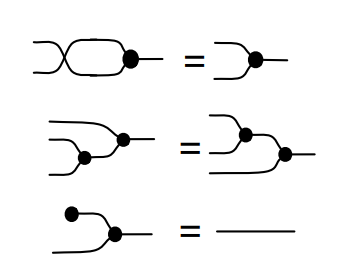
指標の $`\T{sort}`$ 宣言で、ワイヤーの種類(あるいは色)が宣言されます。ワイヤーは一種類(一色)しかないので、絵では黒いワイヤーだけで済みます。指標の $`\T{operation}`$ 宣言で、演算が宣言されています。乗法 $`m`$ を、絵では三本脚の黒丸、単位 $`e`$ を一本脚の黒丸で表現します。等式的法則は、絵でもイコールで書かれていますが、左の図を右の図に変形〈書き換え | 描き換え〉するともみなせます。この例では双方向変形が可能です。
法則をテキストで書くのか、図の変形(あるいは絵等式)で描くのかは表現の手法の違いに過ぎません。内容的にはまったく同じことです。つまり、描画のためのツールバッグと指標は(表現手法以外は)同じものです。
ツールバッグ、つまり、ワイヤー(の色)、ボックス、図の変形の絵による宣言は、やはり描くのが面倒です。なので、テキスト形式の指標が多用されることになりますが、指標と描画のためのツールバッグは同じなんだ! と認識することが大事です。表現手法の違い(どうでもいい!)に惑わされていては、抽象的共通性が見えてきません。
なお、ツールバッグのテキスト表現である指標については、次の過去記事で説明しています。
穴、境界、ストリング図テンプレート
キャンバス上に配置されたボックスは、何かしらの内容〈値 | セマンティクス〉を持つとみなされるのが普通です。が、ボックスに内容が無くて(空虚)、そこに穴があいているとみなすこともあります。ソリッド(中身が詰まっている)か空虚〈hollow〉なのかは、絵で区別するのは難しいことがあります。次の絵は過去記事「モノイド圏上のテンプレート・オペラッド:具体例とソフトウェア的解釈」に載せたもので、キャンバスをピンク色に塗ることにより、穴とソリッドなボックスを区別しています。
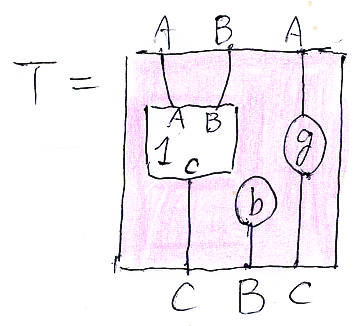
矩形キャンバス上に、1つの穴と2つのソリッドなボックスがあります。穴は番号で識別し、ソリッドなボックスに付いているラベルはその内容〈値 | セマンティクス〉です。
穴は内容〈中身〉を持ちませんが、境界は持ちます。境界上にはプロファイル情報が乗っています。上の図の穴 1 (1 しかないが)のプロファイルは $`(A, B)\to C`$ と書けます。横並びワイヤーが直積を表すなら $`A\times B \to C`$ と解釈できます。ソリッドなボックスはもちろんプロファイルを持ちます。
とても重要だが忘れがちなのは、キャンバス境界もプロファイルを持つことです。上の絵の矩形キャンバスの境界である四辺形は、$`(A, B, A) \to (C, B, C)`$ というプロファイルを持ちます。横並びワイヤーが直積を表すなら $`A\times B\times A \to C\times B\times C`$ ですね。
穴を持つストリング図は、最初から穴があいたキャンバス(穴あきキャンバス)があり、そこにストリング図を描いたとも考えられます。次の絵は過去記事「オペラッドと型付きラムダ計算」に載せたもので、2つ穴あきの円板キャンバスです。
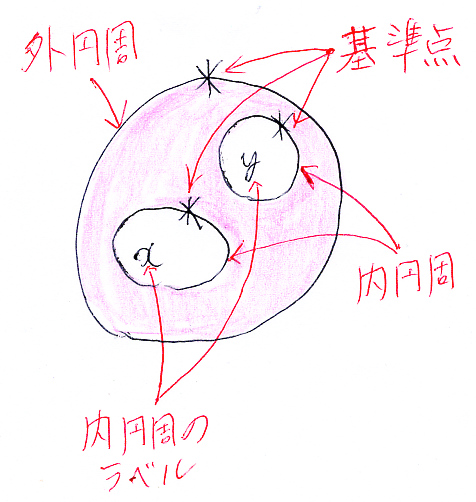
穴あきキャンバスに描いたストリング図、あるいは空虚なボックス〈hollow box〉を持つストリング図はストリング図テンプレート〈string diagram template〉と呼びます。
ストリング図テンプレートの穴を埋めることにより穴のないストリング図を完成させたり、穴に別なストリング図をはめ込んで入れ子のストリング図〈nested string diagram〉を構成したりできます。
円板に穴があいたストリング図テンプレートは、連続同相変形することにより、幹・枝がパイプ状のツリーにできます。例えば、以下は3つの穴を持つ円板形状ストリング図テンプレートです。
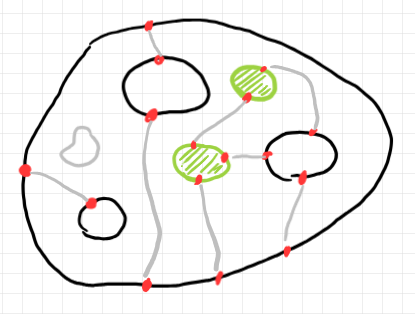
これを連続同相変形すると、次のようなパイプ・ツリーになります。
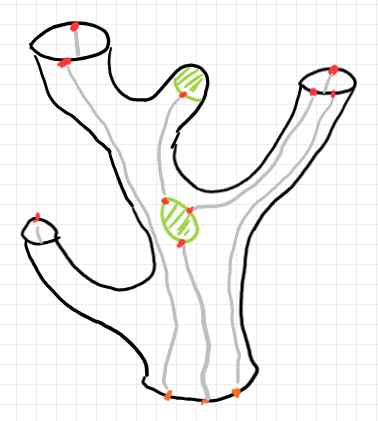
パイプ・ツリーの形に描き直すことにより、テンプレートの穴埋めがオペラッド結合〈operad composition〉であることが容易に分かります。詳しくは次の過去記事を参照してください。
ストリング図テンプレートは、変数を持つ式の絵図版です。穴埋めは変数への代入に対応します。変数と代入がなかったら代数計算がちっとも出来ないですよね。同様に、ストリング図テンプレートは、絵図計算〈絵算〉に無くてはならないものです。
おわりに
以上、ストリング図動画、キャンバス、ツールバッグ、ストリング図テンプレートと、とても重要なのに見逃されがちな概念について説明しました。便利なツールバッグを準備すること、ツールバッグを使ってストリング図/ストリング図動画を創作すること、半完成品としてのストリング図テンプレートを提供すること -- いずれも重要で楽しい作業です。みんな、ストリング図を使おうぜ。
*1:https://beta.homotopy.io/ は専用ツールと言えますが、描画能力も使い勝手もまだまだです。
*2:僕は爺さんなので実物を見たことがあります。映画館で35ミリフィルムのリールを見たことがあるし、自分で8ミリ映画を撮ったこともあります。
*3:3次元空間内の結び目/絡み目を、2次元に射影した図ですが、立体交差の情報が残っているので、純粋に2次元ではありません。
*4:1次元空間には2つの方向〈direction〉があります。n次元空間には方向をうまく定義できませんが2つの向き〈orientation〉は決まります。0次元空間でも2つの向きを持ちます。1次元空間では、方向と向きの区別は不要です。「n次元空間の境界の向き」参照。
*5:製品(ツールバック 折りたたみ): https://www.monotaro.com/p/3262/1626/
画像: https://jp.images-monotaro.com/Monotaro3/pi/full/mono32621626-210423-02.jpg (拡張子は.jpgだが、実際はwebp画像)
*6:モノイド積の結合律子〈associator〉と単位律子〈unitor〉は省略しています。
