インド、ロシアだけじゃないぞ、ブラジル発の熱帯式算数もあるんだぜ

一昨日のエントリーで、ロシア発のマスロフ式算数を紹介しました。実はこれ、リトヴィノフ（G. L. Litvinov）のサーベイ論文"MASLOV DEQUANTIZATION, IDEMPOTENT AND TROPICAL MATHEMATICS: A BRIEF INTRODUCTION"（http://glitvinov.googlepages.com/2007_JMS_426.pdf）の0.2%ほどを解説したものでした。

リトヴィノフ論文のタイトルにTROPICALって単語が入ってるのに気がつきましたか？ロシアのマスロフとはまた別に、ブラジルのシモン（Imre Simon）*1に始まると言われる熱帯風（トロピカル）な計算体系があります（トロピカルというネーミングは、ペリン（Dominic Perrin）によるそうです）。

トロピカルという用語の使用法は現状混乱ぎみですが、ここではとりあえず、max演算と足し算を備えた計算体系を熱帯式算数と呼ぶことにします*2。このエントリーの後半では、熱帯式算数の定義を少し拡張します。

熱帯式算数（ブラジル発）は、一昨日説明したマスロフ式算数（ロシア発）と強い関係があります（2つは二卵性双生児と言ってもいいくらいです）。そこで今回は、熱帯式算数を導入し、マスロフ式算数と熱帯式算数を結びつける変換について述べます。予備知識は「マスロフ式算数がやたらに面白いんですけど」と、（たぶん高校で習う）指数・対数の計算です。

内容：

max演算は、足し算に対しても分配する
これが熱帯式算数だ
マスロフ式から熱帯式への変換
対数マスロフ和＝熱帯和をさぐる
パラメータを持った熱帯式算数
マスロフ式算数と熱帯式算数
算数の先になにがある

●max演算は、足し算に対しても分配する

max(a, b) を a∨b と書くことにすると、

a∨b = b∨a （交換法則）
(a∨b)∨c = b∨(a∨c) （結合法則）
a×(b∨c) = (a×b)∨(a×c) （分配法則）

が成立するのでした。3番目の分配法則を実際に示すと：



b≦c のとき：

cのほうが大きい（正確には小さくない）ので、max(b, c) = c、

よって、左辺 = a×(b∨c) = a×max(b, c) = a×c 。

aは正で b≦c だから、a×b ≦ a×c、

よって、右辺 = (a×b)∨(a×c) = max(a×b, a×c) = a×c 。

以上より、左辺 = 右辺。
c≦b のとき：

同様。

こここでキーになっているのは、aが正という条件のもとで「b≦c ならば、a×b≦a×c」という性質です。aが負になると、掛け算で不等号の向きが保存されないのでダメですけどね。

さて、「b≦c ならば、a×b≦a×c」の×（掛ける）を+（足す）に変えた「b≦c ならば、a+b≦a+c」も成立します。しかも、「aが正」という条件が不要になります。となると、次の分配法則が（aに関する条件なしで）成立します。

a+(b∨c) = (a+b)∨(a+c) （足し算に対する分配法則）

我々は、掛け算に対する分配法則には十分慣れていますが、足し算が分配する状況には慣れてません。そのため、違和感を感じたり困惑したりします。が、「足し算が掛け算である世界」でしばらく計算すれば慣れてきます。「足し算が掛け算である世界」を支配する法則は：

a∨b = b∨a （交換法則）
(a∨b)∨c = b∨(a∨c) （結合法則）
a+(b∨c) = (a+b)∨(a+c) （足し算に対する分配法則）

小学校3年生くらいの計算ドリルを、+→∨、×→+ と置き換えて練習するといいでしょう。僕の場合、「お父さん、その計算全部間違っているよ」とか言われそうですが。

●これが熱帯式算数だ

前節で述べた∨と+の計算体系が熱帯式算数です。マスロフ式算数では、「数は正の数だけ」という制限を付けましたが、熱帯式算数では、ゼロも負の数も自由に使えます。まとめておけば：

熱帯式算数の数（すう、かず）は、任意の実数（特に制限なし）
熱帯式算数の足し数はmax演算
熱帯式算数の掛け算は足し算

「掛け算は足し算」というフレーズが実に奇妙ですが、「熱帯式の計算体系における掛け算は、普通の算数の足し算だ」と言っているのです。

熱帯式算数には、いろいろな変種があります。max演算の代わりにmin演算を使うバージョンがあります。実数ではなくて自然数や整数（離散値）だけを扱うこともあります。+∞や-∞を、数の仲間と認める場合も多いです（そのほうが便利なんです）。

元祖・熱帯式算数は、数として自然数と+∞を考えて、min演算を足し算とするものでした。max演算はmin演算の逆なので、max演算を使うバージョンを極地算数（polar algebra）と呼んだりもしますが、寒そう。寒いの嫌い。最近の傾向は、あまり細かく分類はしないで、max演算またはmin演算と足し算による計算体系を総称して熱帯式（トロピカル）と呼ぶようです。

●マスロフ式から熱帯式への変換

ここから先は紙と鉛筆で計算を追ってみてください。

マスロフ式算数の舞台となる「正の実数の全体」をPと書きます。PositiveのPです。熱帯式算数の舞台となる「（任意の）実数の全体」をRと書きます。RealのRです。

対数関数 log:P→R は、P上の掛け算に関するものごとを、ことごとくR上の足し算に関するものごとに移し（写し）ます。

log(x₁×x₂) = log(x₁) + log(x₂)
log(1) = 0
log(1/x) = -log(x)
log(x^a) = a×log(x)

掛け算の世界	足し算の世界
掛け算 ×	足し算 +
イチ 1	ゼロ 0
逆数 1/x	反数 -y
a乗 x^a	a倍 a×y

対数関数のグラフ：

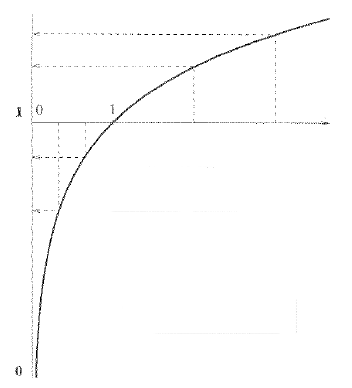
ところで、熱帯式算数では、普通の足し算が掛け算なのでした。よって、対数関数を「マスロフ式 → 熱帯式」という計算体系のあいだの写像と考えると、掛け算を掛け算に写しているのです。

なまじ、お馴染みの足し算記号+（プラス）を使っていると混乱するので、+の代わりに◎を使い、◎を熱帯式掛け算と呼ぶましょう。すると、対数関数logは、普通の掛け算＝マスロフ式掛け算を、熱帯式掛け算に写すことになります*3。等式で書けば：

log(x₁×x₂) = log(x₁)◎log(x₂)

●対数マスロフ和＝熱帯和をさぐる

マスロフ式算数では、ただ1つの計算体系を扱うのではなくて、kでパラメータ付けられたたくさんの足し算 [+]_k が登場します。kを決める（例えばk = 2）ごとにマスロフ式算数が１つ決まります。そして、k→+∞の極限において、マスロフ和 [+]_k はmax演算に移行します。

熱帯式算数でも、パラメータ付けられたたくさんの足し算を考えて、その極限としてmax演算が得られるといいですね。それができるかどうか、ちょっと探りを入れてみましょう。本来、熱帯算数の和（足し算）はmax演算ですが、以下では、max演算に似た足し算的演算を熱帯和と呼ぶことにします。

k-マスロフ和 [+]_k に対応するk-熱帯和があると仮定して、それを △_k としましょう。対数関数logにより、マスロフ掛け算（普通の掛け算）×が熱帯掛け算◎（普通の足し算）に写り、k-マスロフ和[+]_kがk-熱帯和△_kに写るとします。つまり、

log(a×b) = log(a)◎log(b)
log(a [+]_k b) = log(a) △_k log(b)

と仮定します。1番目は既に成立している事実です。2番目は作業仮説です。

ここで、log(a) = A, log(b) = B と置きます。対数関数logと指数関数expは互いに逆関数なので、a = exp(A) = e^A, b = exp(B) = e^B です。この置き換えを使って2番目の等式を書き換えると：

log(e^A [+]_k e^B) = A △_k B

この等式を、左右ひっくり返して：

A △_k B = log(e^A [+]_k e^B)

ここで立場と気分を変えて、この等式は A △_k B を定義するものだとみなしましょう。そうなると、なにも大文字A, Bを使う必要もないので、

a △_k b = log(e^a [+]_k e^b)

定義式としてはこれでもいいのですが、左辺をもう少し簡略化しておいたほうが便利です。マスロフ和の定義と対数の性質を使って書き換えれば：



  log(e^a [+]_k e^b)

= log[((e^a)^k + (e^b)^k)^1/k]

= (1/k)×log[(e^k)^a + (e^k)^b]

e^k = exp(k) は定数なので、これをtと置きましょう。逆に解けば k = log(t) ってことです。kを消してtだけで書けば、



  (1/k)×log[(e^k)^a + (e^k)^b] 

= (1/log(t))×log(t^a + t^b)

だいぶ簡単になったような気がしますが、(1/log(t))が邪魔な感じがします。が、対数の底の変換公式により、(1/log(t))×log(X) = log_t(X) と簡略化できる*4ので、結局：

a △_k b = log_t(t^a + t^b)

k = log(t) だったので、△_log(t) を改めて □_tとでも置けば、

a □_t b = log_t(t^a + t^b)

と、パラメータtを含んだ和が定義されました。マスロフ和の対数バージョンである□_tこそ、我々が求めていた熱帯和＝熱帯式算数の足し算です。

●パラメータを持った熱帯式算数

前節の議論はさぐりを入れる（発見的な）推論だったので、a □_t b = log_t(t^a + t^b) から新たに出発して、次の法則を示す必要があります。

a □_t b = b □_t a （交換法則）
(a □_t b) □_t c = a □_t (b □_t c) （結合法則）
a◎(b □_t c) = (a◎b) □_t (a◎c) （分配法則）

繰り返しますが、ここで出てきた◎は熱帯式掛け算、実は普通の足し算です。これらの法則が示せれば（練習問題！）、tを決める（例えば t = 2）ごとに、熱帯和□_tが決まり、熱帯式算数が得られます。

熱帯式算数は、P上のマスロフ式算数を対数関数でR上にそっくり写したものでした。

log(a×b) = log(a)◎log(b)
log(a [+]_k b) = log(a) □_t log(b) （ただし、t = exp(k)）

ですから、実を言えば、マスロフ式算数で成立する法則の対数バージョンは自動的に成立します。例えば、スケール反転公式

(a [+]_k b)^-1 = a^-1 [+]_-k b^-1

の対数バージョン（熱帯式算数における対応物）は次です。

-(a □_t b) = (-a) □_1/t (-b)

●マスロフ式算数と熱帯式算数

熱帯式算数は、足し算が□_t、掛け算が◎（実は普通の足し算）で与えられる計算体系です。パラメータtを含んでいるので、tの値ごとに計算体系＝算数が決まります。t→+∞のときの極限は、max演算による熱帯式算数となります。そして、t→+0のときの極限は、min演算による熱帯式算数となります。この事実は、□_tの定義から直接示してもいいし、マスロフ式算数の結果を対数関数logにより熱帯式算数に翻訳してもいいです。

今まで述べたことをまとめれば：



                    log→

k-マスロフ式算数 ←------→ t-熱帯式算数 （t = exp(k)）

  |                ←exp       |

  |極限移行                    |極限移行

  |k→+∞                      |t→+∞

  |                            |

  v                log→       v

∨と×の算数    ←------→  ∨と◎の算数

                  ←exp

●算数の先になにがある

マスロフ式算数も熱帯式算数も、文字通り算数、つまり足し算と掛け算の計算体系です。パラメータkやtを極限移行（k→+∞, k→-∞, t→+∞, t→+0）すると、脱量子化（dequantization）されてmaxやminの算数になります。

足し算と掛け算ができれば、それをもとにベクトルや行列の計算もできます。微積分もできます。さらにそれらを道具として力学のような物理的応用もできるでしょう。ただし、そもそもが奇妙な計算をベースにしているので、奇妙な力学などが出現します。

その奇妙さが、量子化ではなくて脱量子化（ブランク定数≠1）から出現するのが興味深いですね。マスロフ達が「古典的」とか「古典化」という用語を使わなかったのは、「よく知られた／なじみ深い」と誤解されないようにでしょうか。脱量子化した世界は、あまり知られてなかった目新しい世界です。

*1:毎度のことながら、人名のカタカナ表記には悩む。Simonを見て僕は、「サイモンとガーファンクル」と「四谷シモン」を思い浮かべたのですが、Imre Simonさんがサイモンかシモンかわからなーい。ポルトガル語に関するhttp://d.hatena.ne.jp/kazsa/20070906/1189095722 とか、スペイン語に関するhttp://ja.wikipedia.org/wiki/%E3%82%B9%E3%83%9A%E3%82%A4%E3%83%B3%E8%AA%9E%E3%81%AE%E6%97%A5%E6%9C%AC%E8%AA%9E%E8%A1%A8%E8%A8%98 とか見て、シモンの可能性が高いと判断。

*2:標準的用語法では、max-plus代数、熱帯代数（tropical algebra）、熱帯半環（tropical semiring）などと呼びます。

*3:ここでは、k-マスロフ代数は (P, [+]_k, ×) で決まり、（狭義の）熱帯代数は (R, ∨, ◎) であるとします。

*4:底の変換公式って、人生ではじめて使った気がする。