石井君*1が、2月19日セミナーのツイン・ホワイトボードを撮影してくれていたので、ハイライト(?)部分を紙芝居にしました。
紙と鉛筆の準備はいいかな -- では、はじまりはじまり。
g = <a, b, x| a*x + b> という関数があるとき、これを2回“ラムダ抽象”してみます。ラムダ抽象とは、右肩ハット(^)または大文字ラムダ(Λ)で表されるオペレータです。ラムダ抽象とカリー化は同義語です*2。ラムダ抽象すると、n引数関数は(n-1)引数関数に変化し、その代わり戻り値が関数型になります。ただし、ここで言う「関数型」は数学的な関数の型ではなくて、とある実行エンジンEで実行する関数コードのデータ型のことです。
gの2回ラムダ抽象g^^を絵に描くとこうです。
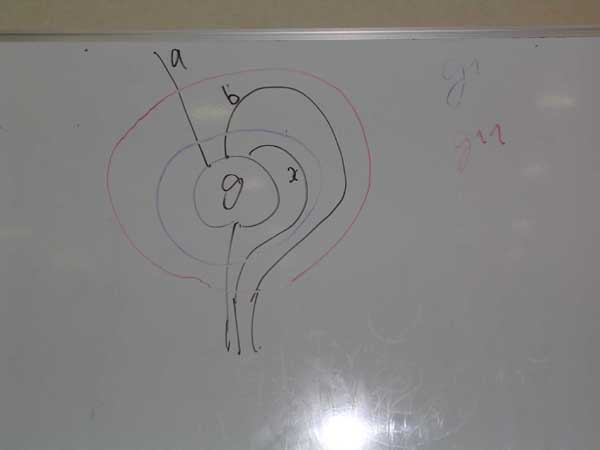
gの1回ラムダ抽象 g^ = Λg と、gの2回ラムダ抽象 g^^ = Λ(Λg) を計算してみます。Λの計算規則*3を使えば、こうなって、こうして、こうですね(ホワイトボード 1行から4行)。
さて、出来上がった g^^ = <a| λb.λx.(a*x + b)> は1引数(変数a)の関数なので、具体的な引数値(実引数)として値3を渡してみましょう(5行目)。
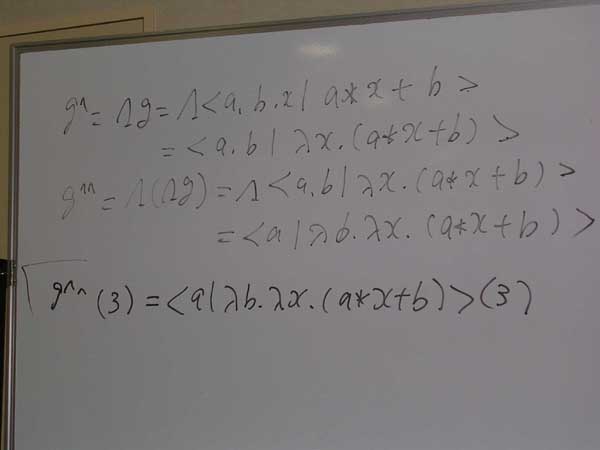
変数aが3に具体化されて、小さなラムダ式が値として吐き出されます。g^^(3) = λb.λx.(3*x + b) ですね。小さなラムダ式が、g^^の戻り値として出力されるわけです。
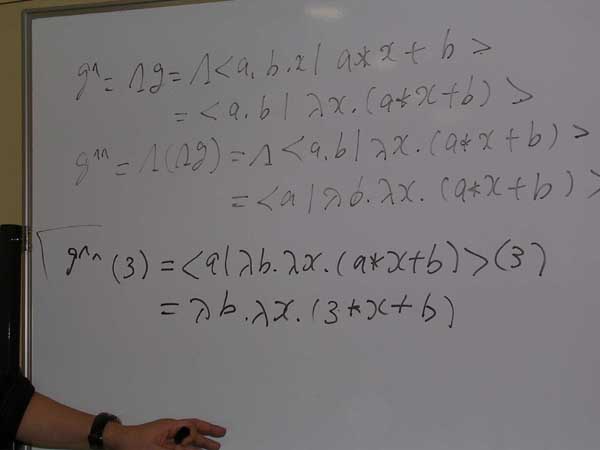
λb.λx.(3*x + b) のbを5に具体化しましょう。(λb.λx.(3*x + b))(5) ってしたくなるでしょうが、それは出来ませんよ。小さいラムダ式はこれ自体としては関数(働き、入力と出力を持つ箱)じゃありませんから。実行エンジンEの第1引数となるべきデータなんです。セミナー第1回を受けた方は、箱とカードの区別を思い出してね。
実行エンジンEを経由して、g^^(3) = λb.λx.(3*x + b) に引数5を渡します。E(g^^(3), 5) ですね。
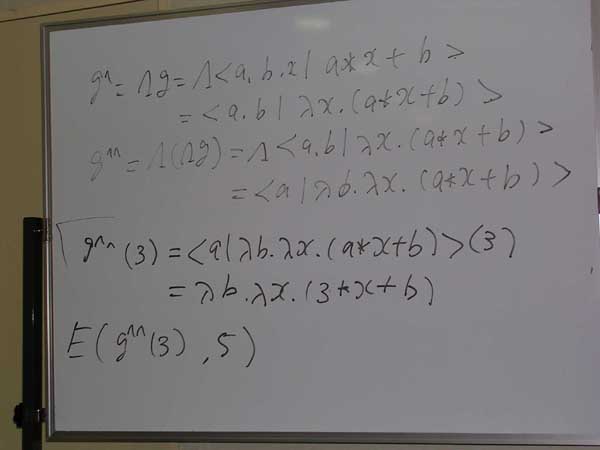
基本等式を使うと、 E(g^^(3), 5) = g^(3, 5) = <a, b| λx.(a*x + b)>(3, 5) である点にも注意。
g^^(3)に具体的引数5が渡るところを絵で描いてみると、こんな。
下側のオダング(光っちゃっている場所)は実行エンジンEです。Eの第2引数(右側のワイヤー)として5を入力すると、結果的に g^^(3) = λb.λx.(3*x + b) のbが5に具体化されます。
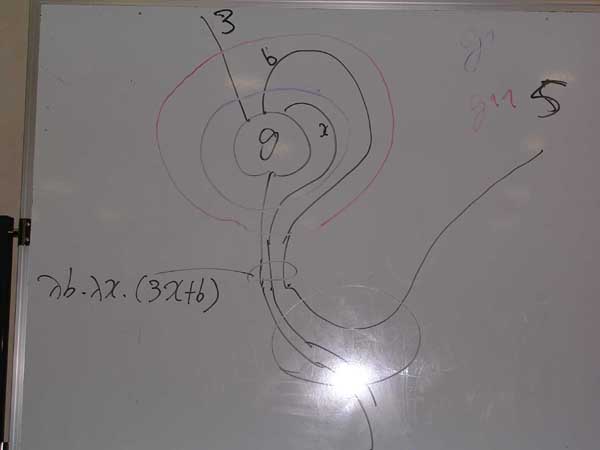
曲がったワイヤーを伸ばしてしまうと、Eを経由して5を渡したE(g^(3), 5)と、直接右上から5を流し込んだg^(3, 5)は同じでしょ、ホラ。

bが5に具体化されたので、λx.(3*x + 5)という小さなラムダ式が出現しました。これは、変数xだけを持つ1次関数を表します。でも正確にいうと、「1次関数を表す関数コード」なので、実行エンジンEを経由しないと評価できません。
もう一度Eを使って、xの具体的な値として7を渡しましょう。
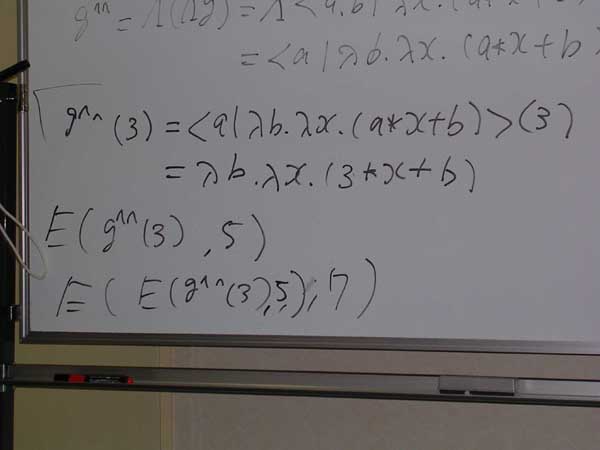
絵はこんな。
3*x + 5 のxに具体的な値7が渡されますよ。ワイヤーを伸ばせばもちろん、g(3, 5, 7)ですから、もとの関数gに3つの実引数を同時に渡したのと同じです。

3*7 + 5 を実際に計算すれば、g(3, 5, 7) = E(g^(3, 5), 7) = E(E(g^^(3), 5), 7) = 26 です。もう少し詳しく書けば:
<a, b, x| a*x + b>(3, 5, 7)
= E(<a, b| λx.(a*x + b)>(3, 5), 7)
= E(E(<a| λb.λx.(a*x + b)>(3), 5), 7)
= E(E(λb.λx.(3*x + b), 5), 7)
= E(λx.(3*x + 5), 7)
= 3*7 + 5
= 26
Eを中置演算子「・」に置き換えて後半の計算を再掲すると、次のようです(リアルワールド向けラムダ計算も参照)。
= (λb.λx.(3*x + b))・5・7
= (λx.(3*x + 5))・7
= 3*7 + 5
= 26
大きなラムダ式は、リアルな、今そこに居る関数の表現。大きなラムダ式=リアルな関数から吐き出される値である小さなラムダ式は、関数コードというデータであり、実行エンジンEに渡すと評価(eval, exec, run)されます。
オマケの説明: λb.λx.(a*x + b) のように自由変数(この場合はa)を含む小さなラムダ式は、大きなラムダ式のボディ内には存在できますが、大きなラムダ式の外に出ることはできないのです。「小さなラムダ式の自由変数=大きなラムダ式の引数変数」になっています。小さなラムダ式の自由変数がすべて束縛されたとき、大きなラムダ式=関数の箱から外にプイッと吐き出されます。もし、自由変数が残った状態(開いたまま)で小さなラムダ式が外に出てしまったら、それを解釈する実行エンジンが途方にくれてしまいますからね*4。