このブログの更新は Twitterアカウント @m_hiyama で通知されます。
Follow @m_hiyama

メールでのご連絡は hiyama{at}chimaira{dot}org まで。

はじめてのメールはスパムと判定されることがあります。最初は、信頼されているドメインから差し障りのない文面を送っていただけると、スパムと判定されにくいと思います。

［参照用 記事］

ホップ代数の絵算 2：割り算と逆元

雑記／備忘

準備が済んだので、絵による計算を試してみましょう。

算数の場合、aをbで割ると a÷b = a/b ですが、a/bは、bの逆数1/bをaにかけ算したモノとみなせます。a/b = a×(1/b) ですね。逆数をかけ算する操作を使うと、a×b = 1 を仮定して、(a×b)×(1/b) = 1×(1/b) なので a = 1/b が出ます。つまり「a×b = 1 ⇒ a = 1/b」。これとまったく同じことを、対称モノイド圏内のホップ代数（群）に対して示します。

内容：

  1. 状況の設定
  2. 絵算のためのチートシート
  3. 絵算の簡単な例
  4. 割り算の定理
  5. 割り算の定理についてもう少し

状況の設定

C（イタリック使ってるぞ！*1）を対称モノイド圏とします。圏Cのモノイド積は×、モノイド単位は1で表します。つまり、C = (C, ×, 1, σ) です。最後のσは対称（symmetry, symmetric braiding）です。

Cではさらに、圏全体で余乗法（対角）Δと余単位!が定義されているとします。「圏全体で」とは、Cの任意の対象Aに対して (A, ΔA, !A) が余モノイドになり、Cの任意の射が余モノイド射となることです。要するに、余モノイド構造は、背景圏（環境圏； background category, ambient category）に前もって備わっていると考えます。典型的具体例は、集合圏における直積の対角Δと終対象への唯一の射!です。

σ、Δ、！ には、ほんとは右下添字が付きます。σA,B:A×B→B×A、ΔA:A→A×A、!A:A→1 という具合。でも、めんどくさいのでたいていは省略。その他エエカゲンな記法を使いますので、律儀な人は注意したほうがいいかも知れません。

H = (H, ∇, i, S) が圏C内のホップ代数（＝群）とします。∇:H×H→H は乗法、i:1→H は単位、S:H→H は対蹠（逆元）です。余モノイド（余代数）構造 (H, Δ, !) にはいちいち言及しません。今さっき言ったように、最初からΔと！は備わっていると仮定してます。あえて余モノイド構造まで明示するなら、H = (H, Δ, !, ∇, i, S) となります。

f:A→H in C に対して、対蹠Sを後結合して f;S を作れます。これは、集合圏の見慣れた記法で書けば f(x)-1 です。f;S を f-1 と書きたいところですが、逆射と間違いそうなので 1/f と書くことにします。1/f は f;S の略記であり、それ以上の意味はありません。

  • 1/f := f;S （略記の定義）

絵算のためのチートシート

今回使う公理をテキストによる等式として下に列挙しておきます。これらの等式を絵にしておくと、絵算のチートシートに使えます。テキストだとものものしい等式も、絵の変形としては自然なモノです。イコールを使ってますが、実際にはたいてい同型である点に注意してください。

まずは、余乗法Δと余単位！に関して。圏Cの任意の対象の上に、余乗法と余単位による余モノイド構造が載ります。

  • Δ;(Δ×id) = Δ;(id×Δ) [余乗法の余結合律]
  • Δ;(!×id) = id [左余単位律]
  • Δ;(id×!) = id [右余単位律]
  • Δ;(f×f) = f;Δ
  • f;! = !

ホップ代数（群） H = (H, Δ, !, ∇, i, S) は次の法則を満たします。

  • (∇×id);∇ = (id×∇);∇ [乗法の結合律]
  • (i×id);∇ = id [左単位律]
  • (id×i);∇ = id [右単位律]
  • ∇;Δ = (Δ×Δ);(id×σ×id);(∇×∇) [双代数法則]

[追記]「双モノイドの簡単な例」でも引用した、ジョン・バエズが使っていた双代数法則の絵を載せます。緑玉＝Δ、赤玉＝∇ です。

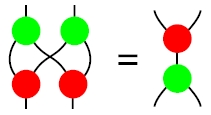
[/追記]

  • Δ;(S×id);∇ = !;i [対蹠の性質 左]
  • Δ;(id×S);∇ = !;i [対蹠の性質 右]

id1, Δ1, !1 のあいだの関係は、ほとんど自明に思える割には厳密な記述がめんどくさいので省略します。

絵算の簡単な例

絵算の小手調べに次の等式を示してみます。

  • Δ;(f×(1/f));∇ = !;i

この等式は、f(x)・f(x)-1 = 1 に相当するものです。次のように示せます。

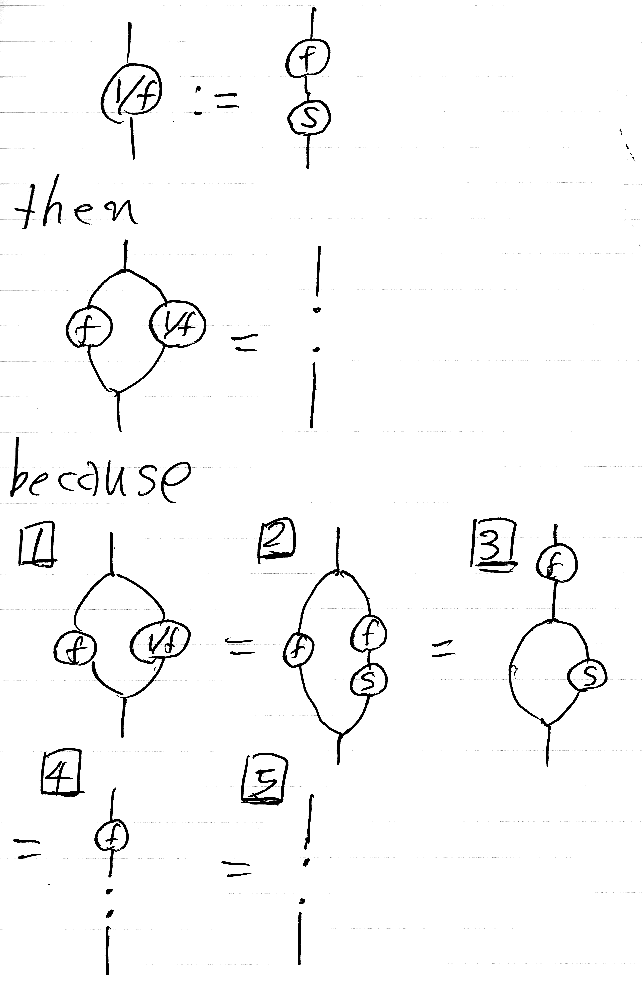
念のため少し説明を加えると：

  1. 1/f をその定義に従い f;S に置き換えます。
  2. Δ;(f×f) = f;Δ を使い、fをひとつにまとめます。
  3. Δ;(I×S);∇ = !;i を使い、下側を !;i に置き換えます。
  4. f;! = ! を使い、上側を ! に置き換えます。

割り算の定理

次に、「x・y = 1 ならば、x = y-1 かつ y = x-1」に相当する定理を示します。この主張をホップ代数の言葉で書いてみると次のようです。

  • Δ;(f×g);∇ = !;i ならば、f = 1/g かつ g = 1/f

1/f, 1/g は f;S, g;S の略記に過ぎないことに注意してください。

さて、絵等式と推論図を組み合わせて上記の定理を描けば次のとおり。

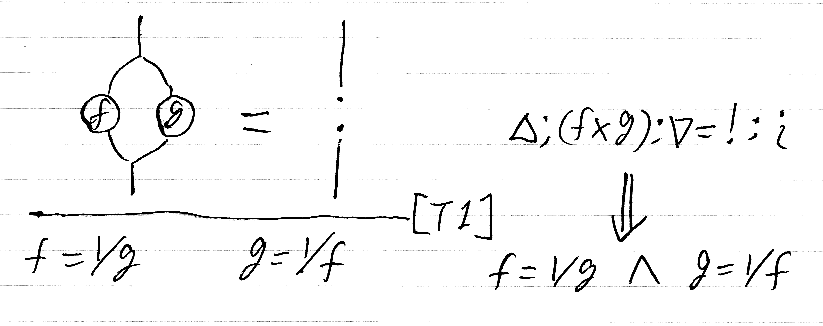
横棒の上側が仮定で、横棒の下側が結論です。[T1]は定理1（Theorem 1）のつもりです。絵の右側には対応するテキスト表現も添えてあります。

定理1は、「x・y = 1 の両辺をyで割ったら x = 1/y で、xで割ったら y = 1/x」に相当するので、割り算の定理とも言えます。この定理1＝割り算の定理をいくつかのステップに分けて示します。

まず、仮定の絵等式の両辺に 1/g を“取り付けます”。等式の左右に同じ工作をしているので等値性は保たれ、結論（横棒の下）が成立します。この推論を[A]とします。なお、ここでは推論（図）と証明（図）を特に区別しません。

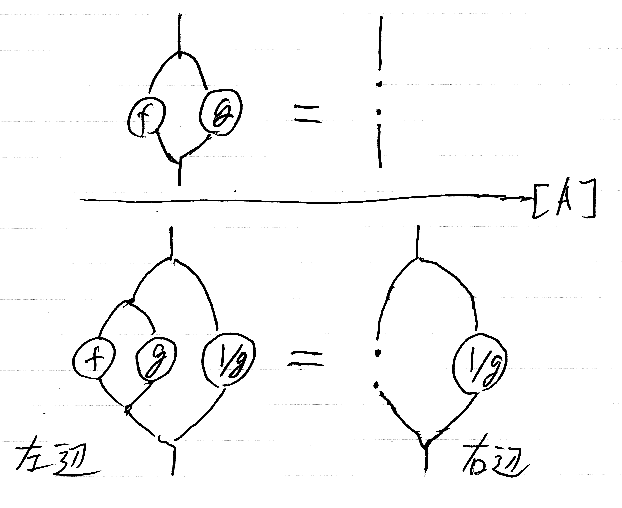
次に、推論[A]の結論（下段）の左辺を変形します。それが次の推論[B]です。推論[B]の結論は、「推論[A]の結論の左辺 = f」となります。

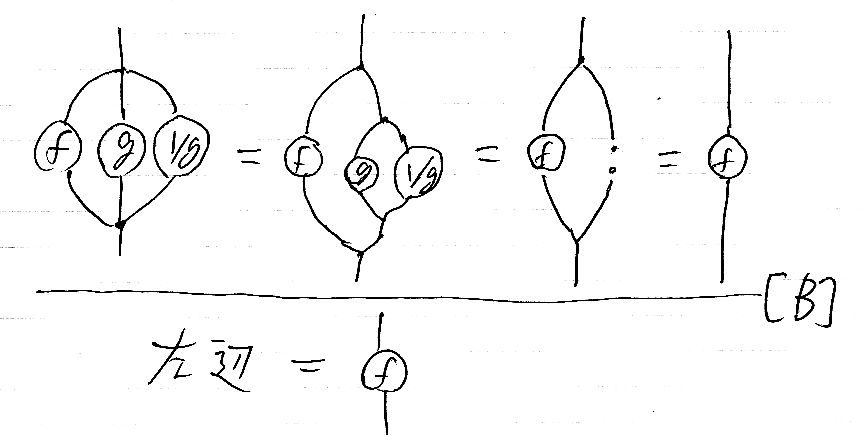
説明を加えます； Δの余結合律と∇の結合律を組み合わせると、一般に次が成立します。Δ3 と ∇3 の意味は、3項の余乗法と乗法です。

  • Δ;([Δ;(f×g);∇]×h);∇ = Δ3;(f×g×h);∇3 = Δ;(f×[Δ;(g×h);∇]);∇

この等式変形で h = 1/g と置いたものが推論[B]の上段左に図示されています。Δ;(g×(1/g));∇ = !;i は最初の計算例で示しているので、左から2番目の絵の一部を !;i で置き換えます。右余単位律と右単位律から !;i は消えてしまい、f が残ります。これで、「推論[A]の結論の左辺 = f」となりました。

推論[C]は、「推論[A]の結論の右辺 = 1/g」を示す推論ですが、簡単ですから省略します。

推論[A]、推論[B]、推論[C]を次のように組み合わせます。

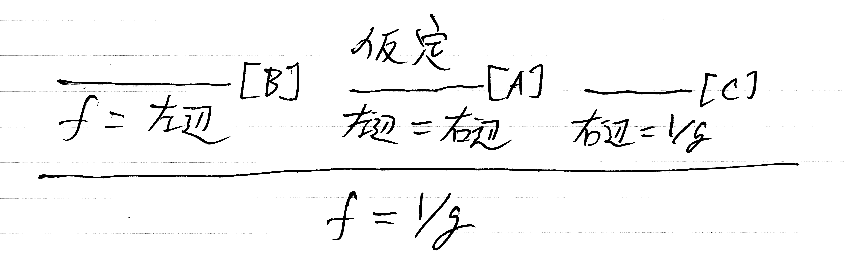
これで、仮定 (Δ;(f×g);∇ = !;i）から f = 1/g を示せました。同様にして、仮定から g = 1/f も示せるので、目的の定理1が証明されました。

  • Δ;(f×g);∇ = !;i ならば、f = 1/g かつ g = 1/f [定理1＝割り算の定理]

割り算の定理についてもう少し

あまりに略記をすると、かえってワケワカンナクなるのですが、試しに簡略な記号法を定義してみます。

まず、Δ;(f×g);∇ を f*g と略記します。f, g :A→H in C のとき、f*g も A→H in C の射となります。f, g, h :A→H in C に対して、(f*g)*h = f*(g*h) （イコールは同型）が成立するので、記号「*」は掛け算と呼んでもいいでしょう。

また、!;i を 1 と略記します。このイチは、あくまで !;i の略記ですよ、混乱・混同をしないように注意してください。1 が一意的に存在するわけではなくて、「Cの対象A」と「Cのホップ代数（群対象）H」ごとに、A→H である 1 が存在します。この事情をハッキリさせたいなら、1A→H とでも書くべきでしょう。

まーともかく、f*1 = 1*f = f （イコールは同型）が成立するので、1 は掛け算「*」の単位になっています。

以上の略記を使って、前節の割り算の定理（定理1）を記述してみましょう。

  • f*g = 1 ならば、 f = 1/g かつ g = 1/f

見た目は算数の話になりました。実際、算数の話も含む定理です。

割り算の定理 f*g = 1 ⇒ (f = 1/g ∧ g = 1/f) はけっこう強力で、ある種の証明原理（proof principle）として使えます。つまり、帰納法の原理などと同様に、ある命題を証明すれば別な命題が自動的に出てくるマシナリーなのです。

割り算の定理の適用例として、対蹠Sが S;S = id であることを示してみましょう。S;S は 1/S と書けますから、id = 1/S を示せばいいですよね。id = 1/S を結論するには id*S = 1 が成立すればOKです。ところが、id*S = 1 とは、Δ;(id×S);∇ = !;i のことなので、問答無用に成立しています。したがって、割り算の定理から、id = 1/S （S;S = id） が結論できます。

もう1回くらい続きます。次はたぶん ∇;S = X;(S×S);∇ を示します。

*1:圏をイタリックにしておかないと、圏の対象として A, B, C とか使えないのです。