余可換コモノイド・モダリティ事件の解説 - 檜山正幸のキマイラ飼育記 (はてなBlog)

一昨日の記事「圏論的モダリティ：圏上の非自然な構造達」の「僕のモダリティ経験」の節で：

試しに、非負実数係数のテンソルの圏に余可換コモノイド・モダリティを入れてみると、そのモダリティと整合する部分圏として部分性と確率的非決定性の両方がうまく定義できるようです。これが分かったとき、僕にとってはA-ha momentでした。

特に役に立つのは、2つの非自然変換から構成される余可換コモノイド・モダリティです。余可換コモノイド・モダリティの事例はそのうち述べるつもりです。

予告に従い、余可換コモノイド・モダリティの事例について述べます。タイトルに「事例」でなく「事件」と付けているのは、これから述べることが僕には思いがけないことだったからです。

内容：

余可換コモノイド・モダリティが定義する部分圏、不思議だ
余可換コモノイド・モダリティ
集合圏の余可換コモノイド・モダリティ
関係圏の余可換コモノイド・モダリティ
モダリティと単葉関係／全域関係
非負実数係数テンソルとその圏
非負実数テンソルの圏の余可換コモノイド・モダリティ
モダリティと非分散テンソル／マルコフ・テンソル
参考文献

余可換コモノイド・モダリティが定義する部分圏、不思議だ

池尻大橋駅から10秒くらいの近さのカフェ・ベローチェで、割と何となくナプキンペーパーで計算していたのですが、計算結果を見て「エッ?!」と驚きました。事前に予想も期待もしてなかった結果だったからです。これが、僕が余可換コモノイド・モダリティに興味を持つキッカケとなった「事件」（大げさだけど）です。詳しい説明は後の節でしますが、概要だけこの節で言っておきます。

係数（成分）が非負実数であるテンソル（幾つかの数を適当な次元の矩形状に並べたモノ）を考えます。非負実数係数のテンソルに関して次の言葉を使いますが、これらは後で定義します。

非分散テンソル（nondispersive tensor）
ブール・テンソル（boolean tensor, Boole tensor）
マルコフ・テンソル（Markov tensor）

すべての非負実数（係数の）テンソルから構成される圏NNTens（non-negative (coefficient) tensors）に、自明と思える簡単なモダリティΔ（余乗法）とε（余単位）を入れると：

Δと整合する射の全体は、非分散ブール・テンソルの全体と一致する。Δと整合する射が作るNNTensの部分圏は、有限集合を対象とする部分写像の圏FinPartialと同型である。
εと整合する射の全体は、マルコフ・テンソルの全体と一致する。εと整合する射が作るNNTensの部分圏は、有限離散測度空間を対象とするマルコフ核（別名 stochastic map/kernel/relation）の圏FinStocと同型である。
Δとεの両方と整合する射の全体は、非分散ブールかつマルコフなテンソルの全体と一致する。Δ, εと整合する射が作るNNTensの部分圏は、有限集合と写像の圏FinSetと同型である。

これと似た結果は関係圏Relでも成立します。関係に関する次の言葉も後で定義します。

単葉（一価）関係（univalent relation）
全域関係（total relation）

Relにおける余乗法と余単位も同じ記号Δ, εで表すとして：

Δと整合する射の全体は、単葉な関係の全体と一致する。Δと整合する射が作るRelの部分圏は、部分写像（partial map）の圏Partialと同型である。
εと整合する射の全体は、全域な関係の全体と一致する。
Δとεの両方と整合する射の全体は、単葉かつ全域な関係の全体と一致する。Δ, εと整合する射が作るRelの部分圏は、集合と写像の圏Setと同型である。

うーん？なんでこんな現象が起きるのだろう？内在的必然性とか背後のメカニズムとかはサッパリ分かりません。不思議だが本当だ。

Δとεの組み合わせは余可換コモノイド・モダリティとなります。経験則として、このモダリティ(Δ, ε)の一部または全部と整合する射を考えることは、面白い部分圏を抽出する手段として有効だ、とは言えそうです。理由は分からんけど。

余可換コモノイド・モダリティ

C = (C, $\otimes$ , I, α, λ, ρ, σ) を対称モノイド圏とします。α, λ, ρはそれぞれ、結合律子（associator）、左単位律子（left unitor）、右単位律子（right unitor）、対称（symmetry）です（律子に関しては「律子からカタストロフへ」を参照）。

一般に、Cの対象Aに対して、自己関手 K_A:C→C はすべての対象をAに移し、すべての射をid_Aに移す“定数関手”とします。また Sq:C→C は、対象も射もモノイド積の意味で平方（二乗）する関手です。

K_A(X) = A, K_A(f) = id_A
Sq(X) = X $\otimes$ X, Sq(f) = f $\otimes$ f

モノイド単位対象Iに対する定数関手K_Iと平方関手Sqを考えます。この2つは、非全域関手ではなくて普通の（全域な）関手です。さらに非自然変換 Δ::Id ?⇒ Sq :C→C と ε::Id ?⇒ K_I :C→C を考えます。ここで、IdはCの恒等関手です。特殊な矢印記号'?⇒'は、非自然（必ずしも自然ではない）ことを表します。このへんのところは「非全域関手と非自然変換」を参照。

非自然変換Δ, εの、対象Xにおける成分は次の形です。

Δ_X:X→X $\otimes$ X in C
ε_X:X→I in C

2つの非自然変換Δとεの組み合わせ(Δ, ε)が余可換コモノイド・モダリティであるとは、任意の対象Xに対して、3つ組 (X, Δ_X, ε_X) が余可換コモノイドになることです。他に、Δとεが圏のモノイド構造と調和するための一貫性条件も要求します。

余可換コモノイドの公理は昨日の記事の「対称モノイド圏の余可換コモノイド・モダリティ」に載せています。ここでは、図を描いておきましょう。余乗法Δは分岐の黒丸、余単位εはストッパーの横棒のアイコンで示すことにします。射の描画方向は ↓→ です。

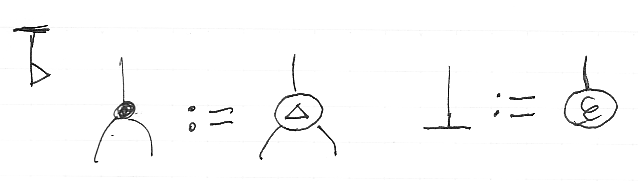
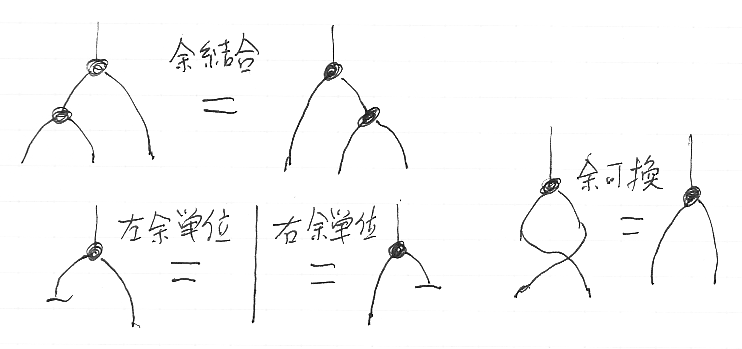
余結合律、左余単位律、右余結合律、余可換律は次のとおりです。id_Xを単にXと書き、律子（構造同型射）α, λ, ρによる細かい調整は省略しています。

Δとεとモノイド積／モノイド単位との一貫性（調和性）は次の等式で表現できます。

Δ_X⊗Y = (Δ_X $\otimes$ Δ_Y);(X $\otimes$ σ_X,Y $\otimes$ Y)
ε_X⊗Y = ε_X $\otimes$ ε_Y
ε_I = id_I

絵なら次のようです。点線は、モノイド単位対象を表す“空なワイヤー”です。

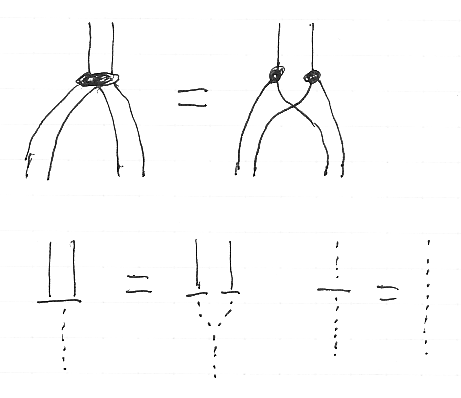
また、f:X→Y in C が“Δと整合すること”と“εと整合すること”は次の図で表せます。

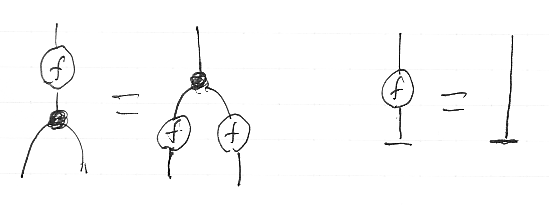
集合圏の余可換コモノイド・モダリティ

集合圏Setに対して、余可換コモノイド・モダリティを定義します。集合圏のモノイド積は直積（記号'×'）、モノイド単位対象は 1 = {0} とします。Δ, εを次のように定義します。

Δ_X:X→X×X, Δ_X(x) = (x, x)
ε_X:X→1, ε_X(x) = 0

集合Xごとの(X, Δ_X, ε_X)が余可換コモノイドになること、そして一貫性条件を満たすことを確認してみてください。

集合圏Setの余可換コモノイド・モダリティでは、すべての射（集合のあいだの写像）がモダリティと整合します。つまり、f:X→Y in Set に対して：

f;Δ_Y = Δ_X;(f×f) : X→Y×Y
f;ε_Y = ε_X : X→1

これも簡単に確認できます。

結局、今定義した集合圏の余可換コモノイド・モダリティ(Δ, ε)では、Δもεも自然変換になります。自然変換は非自然変換の特別なものなので問題はありませんが、モダリティと整合する射として部分圏を抽出することは出来ません。部分圏を作る目的から言えば、自然な全域モダリティは役立たずなのです。

余可換コモノイド・モダリティが自然変換になっている状況は、実はモノイド積が直積（デカルト積）になっている場合に限られます。次の定理があります。

対称モノイド圏Cに余可換コモノイド・モダリティ(Δ, ε)があり、Δとεが自然変換のとき、モノイド積は直積（デカルト積）である。

証明は割愛しますが、このことから、直積ではないモノイド積を持つ対称モノイド圏では、自然変換で与えられる余可換コモノイド・モダリティは存在しないことになります。モダリティが欲しかったら、非自然なものを許すしかないのです。これは、非自然性に関する重要な知見です。

関係圏の余可換コモノイド・モダリティ

次に、関係圏Relに余可換コモノイド・モダリティを入れましょう。関係圏のモノイド積も直積（記号'×'）、モノイド単位対象は 1 = {0} です。Δとεも集合圏と同じですが、表現の仕方は少し違います。

Δ_X:X→(X×X), Δ_X = {(x, (x', x''))∈X×(X×X) | x = x' = x''} = {(x, (x, x))∈X×(X×X) | x∈X}
ε_X:X→1, ε_X = {(x, 0)∈X×1 | xは任意（無条件）} = X×1

集合Xごとの(X, Δ_X, ε_X)が関係圏において余可換コモノイドになることも、そして一貫性も、集合圏のときと同様に確認できます。

集合圏とは違い、関係圏の射はΔ, εと整合するとは限りません。t:{1, 2}→{1, 2} in Rel を次のように定義します。

t = {(1, 1), (1, 2)}

このtでは、t;Δ_{{1, 2}} = Δ_{{1, 2}};(t×t) は成立しないし、t;ε_{{1, 2}} = ε_{{1, 2}} も成立しません。具体的に計算すれば分かります。

t;Δ_{{1, 2}} = {(1, 1), (1, 2)};{(1, (1, 1)), (2, (2, 2))} = {(1, (1, 1)), (1, (2, 2))}
Δ_{{1, 2}};(t×t) = {(1, (1, 1)), (2, (2, 2))};{((1, 1), (1, 1)), ((1, 1), (1, 2)), ((1, 2), (1, 1)), ((1, 2), (1, 2))} = {(1, (1, 1)), (1, (1, 2))}
t;ε_{{1, 2}} = {(1, 1), (1, 2)};{(1, 0), (2, 0)} = {(1, 0)}
ε_{{1, 2}} = {(1, 0), (2, 0)}

以上の計算から、

t;Δ_{{1, 2}} ≠ Δ_{{1, 2}};(t×t)
t;ε_{{1, 2}} ≠ ε_{{1, 2}}

t = {(1, 1), (1, 2)} は、Δともεとも整合しない射です。

モダリティと単葉関係／全域関係

関係圏Relにおいて、どのような射がΔ, εと整合するかを見ておきましょう。

r:X→Y in Rel がΔと整合するとします。このとき、r;Δ_Y = Δ_X;(r×r) : X→Y×Y in Rel が成立します。等式の左辺／右辺を具体的に書き下してみます。

   r;Δ_Y
 = {(x, y)∈X×Y | (x, y)∈r};{(y, (y', y''))∈Y×(Y×Y) | y = y' = y''}
 = {(x, y)∈X×Y | (x, y)∈r};{(y, (y, y'))∈Y×(Y×Y) | y = y'}
 = {(x, (y, y'))∈X×(Y×Y) | (x, y)∈r かつ y = y'}

   Δ_X;(r×r)
 = {(x, (x, x))∈X×(X×X) | x∈X};{((x, x'), (y, y'))∈(X×X)×(Y×Y) | (x, y)∈r かつ (x', y')∈r}
 = {(x, (y, y'))∈X×(Y×Y) | (x, y)∈r かつ (x, y')∈r}

r;Δ_Y = Δ_X;(r×r) であるためには：

(x, y)∈r かつ y = y' ⇔ (x, y)∈r かつ (x, y')∈r

⇒方向は自明なので、実質的な条件は：

(x, y)∈r かつ (x, y')∈r ⇒ y = y'

この条件を満たす関係 r:X→Y in Rel を単葉（univalent, 一価）な関係と呼びます。したがって、

関係rがΔと整合する ⇔ rは単葉関係である

次に、r:X→Y in Rel がεと整合するとします。このとき、r;ε_Y = ε_X : X→1 in Rel が成立します。等式の左辺／右辺を具体的に書き下してみます。

   r;ε_Y
 = {(x, y)∈X×Y | (x, y)∈r};{(y, 0)∈Y×1 | yは任意}
 = {(x, 0)∈X×1 | xに対して、(x, y)∈r となる y∈Y が存在する}

   ε_X
 = {(x, 0)∈X×1 | xは任意}

r;ε_Y = ε_X であるためには：

xに対して、(x, y)∈r となる y∈Y が存在する ⇔ xは任意

言い換えれば：

任意のxに対して、(x, y)∈r となる y∈Y が存在する

この条件を満たす関係 r:X→Y in Rel を全域（total）な関係と呼びます。したがって、

関係rがεと整合する ⇔ rは全域関係である

Δとεの両方と整合する関係（Relの射）は、単葉かつ全域な関係となります。単葉かつ全域な関係は、写像だと思ってもかまいません。つまり、関係圏Relの部分圏として集合と写像の圏を再現しています。この部分圏に制限すれば、Δとεは自然変換になるので、部分圏上に自然な余可換コモノイド・モダリティが載ります。自然な余可換コモノイド・モダリティは直積（デカルト構造）を定義するので、この部分圏に制限したモノイド積が直積を与えることも分かります。

デカルト圏（直積／終対象を持つ圏）と、そのデカルト圏を拡張したモノイド圏の組としてはフレイド圏（Freyd category）があります。余可換コモノイド・モダリティを持った対称モノイド圏は、フレイド圏とかなり似ています。そういえば、フレイド圏に非自然な対角や余対角を載せることはやったことがありました。

プレモノイド圏やバイノイド圏は、関手性が破れた積を扱う仕組みでした。どうも、非関手的（no-fanctorial）／非自然（non-natural）な対応や族を扱う必然性はありそうです。モダリティは、非関手的／非自然な構造を扱う道具になる気がします。

非負実数係数テンソルとその圏

これから、係数（成分）が非負実数であるテンソルと、そのようなテンソルを射とする圏NNTens（category of non-negative tensors）に関して手早く（あるいは雑に）説明します。そして、次のような、特別な種類のテンソルを定義します。

非分散テンソル（nondispersive tensor）
ブール・テンソル（boolean tensor, Boole tensor）
マルコフ・テンソル（Markov tensor）

R_≧0を非負実数の全体とします。以下、X, Y, Zなどは有限集合を表すとします。写像 f:X×Y→R_≧0 を非負実数（係数の）テンソル（non-negative (coefficient) tensor）と呼びます。fをテンソルとして扱うときは、f(x, y)をf[x→y]またはf[x←y]と書くことにします。また、f = (f[x→y] | x∈X, y∈Y) という書き方も用います。これは、行列の成分表示と同じだと思えばいいです。

f = (f[x→y] | x∈X, y∈Y) のテンソルとしてのプロファイルは、X→Y だとします。fは2つの見方ができます。2つの見方を適宜切り替えます。

写像として f:X×Y→R_≧0
テンソルとして f:X→Y

f = (f[x→y] | x∈X, y∈Y), g = (g[y→z] | y∈Y, z∈Z) のテンソルとしての結合f;gは次のように定義します。

(f;g)[x→z] = Σ(y∈Y | f[x→y]g[y→z])

有限集合Xに対する恒等テンソルid_Xは：

id_X[x→x'] = (if x = x' then 1 else 0)

id_Xの成分表示は、クロネッカーのデルタδ[x→x']を使うことも多いです。つまり、id_X = (δ[x→x'] | x∈X, x'∈X) 。

ここまでの定義では、添字集合に任意の有限集合を許した行列とテンソルの差はありません。テンソルと呼ぶのは、X = X₁×...×X_n, Y = Y₁×...×Y_m のようなときに、f = (f[x₁, ..., x_n→y₁, ..., y_m] | x₁∈X₁, ..., x_n∈X_n, y₁∈Y₁, ..., y_m∈Y_m) という表現を使うからです。テンソルの具体的な計算例は、「確率的推論・判断の計算法：マルコフ・テンソル絵算」にあります。ブラケット内の x₁, ..., x_n→y₁, ..., y_m で、矢印よりカンマが優先される（結合度が強い）ので注意してください。

非分散テンソル

f:X→Y in NNTens のとき、a∈X に対して次の性質を定義します。

fがaで消失するとは、すべてのy∈Yに対して、f[a→y] = 0 のこと。
fがaで分散（または分岐）するとは、f[a→y'] ≠ 0 かつ f[a→y''] ≠ 0 かつ y' ≠ y'' であるy', y''が存在すること。

消失と分散を否定すると：

fがaで消失しないとは、f[a→y] ≠ 0 となるyが存在すること。
fがaで分散しない（または分岐しない）とは、任意のy', y''に対して、y' ≠ y'' であるならば、f[a→y'] = 0 または f[a→y''] = 0 となること。

任意のx∈Xに対してxで分散しないテンソルを非分散テンソル（nondispersive tensor）と呼ぶことにします。非分散テンソルは消失を禁止してないので、Xの一部でfは消失しているかも知れません。

ブール・テンソル

テンソルの係数が0か1のどちらかの場合、0をfalse、1をtrueと思うとブール値なので、ブール・テンソル（boolean tensor, Boole tensor）と呼びましょう。ただし、計算はブール値ではなくて非負実数の計算を行うので、1 + 1 = 1 なんてことはありません。このため、ブール・テンソルの結合がブール・テンソルとは限りません。

マルコフ・テンソル（Markov tensor）

テンソル f = (f[x→y] | x∈X, y∈Y) が、任意の x∈X に対して Σ(y∈Y | f[x→y]) = 1 のときマルコフ・テンソル（Markov tensor）と呼びます。「確率的推論・判断の計算法：マルコフ・テンソル絵算」の計算はすべてマルコフ・テンソルの計算です。

非負実数テンソルの圏の余可換コモノイド・モダリティ

非負実数テンソルの圏NNTensに余可換コモノイド・モダリティを入れます。NNTensのモノイド積は、対象に対しては直積（記号'×'）、射に対してはテンソル積（記号' $\otimes$ '）とします。f:X→Y, g:Z→W in NNTens のとき、f $\otimes$ g:X×Z→Y×W は次のように定義されます。

(f $\otimes$ g)[x, z → y, w] = f[x→y]g[z→w]

モノイド単位対象は I = {*} とします。唯一の要素を星印にしているのは、「確率的推論・判断の計算法：マルコフ・テンソル絵算」で使った u[x] = u[*→x] のような書き方に合わせるためです。

余乗法Δと余単位εは次のように定義します。

Δ_X:X→(X×X), Δ_X[x→x', x''] = (if x = x' = x'' then 1 else 0)
ε_X:X→I, ε_X[x→*] = 1

(Δ, ε)が余可換コモノイド・モダリティとなることを示すのは、テンソル計算のよい練習問題です。実際の計算は省略しますが、便利な略記法をここで述べておきます。

テンソルの計算では、しばしば添字を動かした総和をとります。例えば、f:X→Y×Z, g:Y→W, h:Z→W のときに k = f;(g $\otimes$ h) : Z→W×W を計算するとします。k[x→w, w']を求めるには総和と取ります。

k[x→w, w'] = Σ(y∈Y, z∈Z | f[x→y, z]g[y→w]h[z→w'])

このとき、総和を意味するΣを省略して、

k[x→w, w'] = (y, z | f[x→y, z]g[y→w]h[z→w'])

と書きます。これは「アインシュタインの総和規約」ですが、和を取る添字は残しています。和を取る添字を目視で判断するのがそれほど楽でではないからです。次の節の計算ではこの総和規約を使います。

モダリティと非分散テンソル／マルコフ・テンソル

非負実数テンソルの圏NNTensにおいて、どのような射がΔ, εと整合するかを調べます。僕が、池尻大橋カフェ・ベローチェのナプキンペーパーにした計算とは、これから述べる計算です。

f:X→Y in NNTens がΔと整合するとします。このとき、f;Δ_Y = Δ_X;(f×f) : X→Y×Y in NNTens が成立します。等式の左辺／右辺を具体的に書き下してみます。

   (f;Δ_Y)[x→y', y'']
 = (y | f[x→y]Δ[y→y', y''])
 = if y = y' = y'' then f[x, y] else 0

   (Δ_X;(f×f))[x→y', y'']
 = (x', x'' | Δ[x→x', x'']f[x'→y']f[x''→y''])
 = if x = x' = x'' then f[x→y']f[x→y''] else 0

整合性は次の等式となります。

(if y = y' = y'' then f[x, y] else 0) = (if x = x' = x'' then f[x→y']f[x→y''] else 0)

等式の両辺が等しくなるためには、y' = y'' 以外の部分では、(右辺のテンソル)[x→y', y''] = 0 です。したがって、次が成立します。

y' ≠ y'' ならば、f[x→y']f[x→y''] = 0

fの係数（成分）は非負実数なので：

f[x→y']f[x→y''] = 0 ⇔ f[x→y'] = 0 または f[x→y''] = 0

結局、

y' ≠ y'' ならば、 f[x→y'] = 0 または f[x→y''] = 0

これが任意のxに対して成立するので、fは非分散テンソルです。

また、y' = y''（ = y）である部分に関しても、次の制約があります。

f[x, y] = f[x→y']f[x→y'']

y = y' = y'' なので、

f[x, y] = (f[x→y])²

これは、f[x→y] = 0 または f[x→y] = 1 を意味するので、fはブール・テンソルです。

これで、f:X→Y in NNTens がΔと整合することは、fが非分散ブール・テンソルであることだと分かりました。x∈X に対して、f[x→y] = 1 となるyは高々1つで、残りの係数（成分）f[x→y]はすべて0です。

次に、f:X→Y in NNTens がεと整合するときを考えます。そのとき、f;ε_Y = ε_X : X→I in NNTens が成立します。

   (f;ε_Y)[x→*]
 = (y | f[x→y]ε[y→*])
 = (y | f[x→y]ε)

   ε_X[x→*]
 = 1

これより、(y | f[x→y]ε) = 1 がすべての x∈X で成立します。つまり、fはマルコフ・テンソルです。

Δとεの両方と整合するテンソル（NNTensの射）は、非分散ブールかつマルコフなテンソルとなります。これは、x∈X に対して、f[x→y] = 1 となるyは1つだけあり、残りの係数（成分）f[x→y]はすべて0となるテンソルです。

非分散ブールかつマルコフなテンソルとは、有限集合XからYへの写像と同じことです。関係圏の場合と同様に、余可換コモノイド・モダリティ(Δ, ε)と整合する部分圏として（有限）集合と写像の圏が再現します。

参考文献

非負実数テンソルの圏NNTensには余可換コモノイド・モダリティが載ります。余可換コモノイド・モダリティ付きの圏としては、NNTensとRel（関係圏）はかなり類似しています。現象としては「面白いな」と思いますが、たまたまやってみた計算が発端なので、全体の構図は見えません。よく分からなくてモヤモヤしてます。

とりあえず、ヒントになりそうな論文を挙げておきます（過去に言及した論文達ですが）。

Title: Categorical Structure of Asynchrony
Author: Peter Selinger
Pages: 23p
URL: http://www.mathstat.dal.ca/~selinger/papers/catasynch.pdf

古め（1999年）の論文ですが、色々なアイディアや話題が詰め込まれています。セリンガーが対角（diagonals）と呼んでいるものは余可換コモノイド・モダリティです。

Title: Disintegration and Bayesian Inversion, Both Abstractly and Concretely
Authors: Kenta Cho, Bart Jacobs
Pages: 15p
URL: http://www.cs.ru.nl/B.Jacobs/PAPERS/disintegration.pdf

今年（2017年）になって書かれたものだと思います。使われている絵算（pictorial/graphical/diagrammatic calculation）は、余可換コモノイド・モダリティを含むものです。測度論の晦渋な議論に入り込むのを上手に避けながらdisintegrationの計算をしています。