「1年たって、手書きから自動描画へ」で触れたように、Catyに視覚化機能を入れる作業をチョボチョボとやっています。
Catyの計算モデルはもともとが絵算(pictorial/graphical/diagrammatic calculation)なので、視覚化とはいえ、本来の構造を目に見えるようにすればいいだけです(描画のコツは色々必要ですが)。
Catyは、大域脱出や副作用のような不純な計算もサポートしているので、不純計算の視覚化(図示、描画)をどうしようか? という問題があります。結論を言えば、ほとんど省略して描かない方針です。あまり精密に視覚化すると、グラフのノードや辺の数が膨大になってかえってワケわかんなくなる恐れがあるからです。
とはいえ、特定の種類の不純計算を局所的に描くのは有効かもしれません。ここでは、例外を含む計算の描画法と、それに対応する圏論的なモデルを紹介します。計算モデルは、とあるインデックス付き圏(indexed category)*1からグロタンディーク構成(Grothendieck construction)で得られるファイバー圏(fibred/fibered category)になります。
内容:
- 例外を投げるかもしれない計算
- 例外のキャッチと再スロー
- 例外付き計算の結合
- 例外付き計算のインデックス付き圏/グロタンディーク構成
例外を投げるかもしれない計算
まず、A、Bなどはデータ型で、fが純粋計算(pure computing)の計算単位(computational unit)とします。これを f:A→B と書きます。このようなデータ型と計算単位の全体は、計算の直列結合(sequential composition)により圏になります。この圏をCとします。Cは、集合圏の部分圏で実現され、直積や直和も自由に使えるとします。
EをCの部分圏とします。Eは例外型と例外変換の圏です。X∈|E| のとき、型Xのデータは例外発生時に投げる(throwする)ことができます。φ:X→Y in E は、例外データを別な例外データに変換する処理と解釈します。E⊆C を仮定していますが、E = C でもかまいません。JavaScriptは、例外時にどんなデータでも投げられるので E = C の例と考えられます。
データ型Aを入力とする計算単位fが正常終了時にデータ型Bを出力し、異常終了(例外)時には例外型Xを投げることは、次のように図示できます。
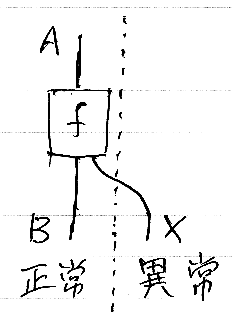
以下では、圏Eの対象である例外型を X, Y などで、Eの射である例外変換を φ, ψ などで表すことにします。
例外のキャッチと再スロー
先の図示法に従うと、射の向きは上から下、正常出力が左のワイヤー、例外(異常)出力が右のワイヤーに流れます。例外をキャッチすると、いったん異常の世界に飛んでいった出力ワイヤーを正常の世界に戻せます。例外キャッチは、次の図の右から左に曲がったワイヤー部分で表現できます。
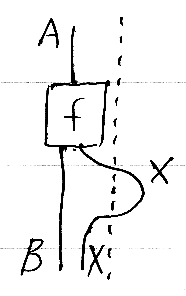
次の擬似コードで雰囲気は分かるでしょう。
// f:A -> B throws Xtry {f} catch (x : X) {return x}
正常と例外を一緒にした出力型は、B + X となります。ここで「+」は直和(ユニオン型、バリアント型)です。ただし、通常の直和のような対称性はないので、B +: X と記すことにします。コロンがある側に例外型を書きます。
この記法を使うと、計算単位fのプロファイル(入出力仕様)は次のようになります。
- f: A → B +: X
「→ B +: X」は、「returns B, throws X」と読むといいかもしれません。
try{f} のプロファイルは、A → B + X となります。単なるプラス記号は正常値どうしの直和です。例外はなくなるので、A → (B + X) +: 0 と書くとより正確です。0は空集合を表しますが、neverとかnothingと読み下すとよいでしょう。「→ (B + X) +: 0」の読み方は「returns (B or X), throws nothing」です(正確には、orよりはxor)。
さて、いったんキャッチした例外に例外変換をかけて再スローする処理を考えてみましょう。f: X → B +: X のXに、例外変換 φ: X → Y を組み合わせます。
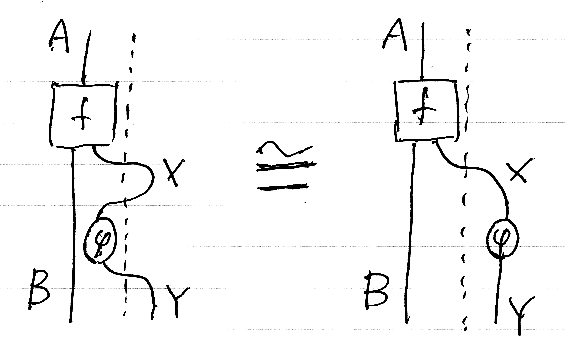
上の図の左側は次の擬似コードで表すことができます。
// f:A -> B throws X
// φ:X -> Ytry {f} catch (x : X) {throw φ(x)}
キャッチと再スローをしてますが、概念的にはこのような異常世界/正常世界の行ったり来たりは不要で、異常世界(点線の右)のなかでデータ変換をすればいいだけです。上の図の右側が単純化した処理を表しています。例外処理をブラックボックスに閉じ込めれば、図の左右の違いは分からなくなり同値です。
fで発生した例外をφで変換するような計算処理を (f, :φ) という記号で表すことにします。f: A → B +: X ならば、(f, :φ): A → B +: Y となります。プロファイルの例外型の部分が、XからYに置き換わります。
例外付き計算の結合
2つの例外付き計算 f: A→ B +: X と g: B→ C +: Y の結合の話題は何度もしています。モナドを使うのが一番スッキリするでしょう; 直和に関するモノイド (X, ∇, iX) を考えます。∇X: X + X → X は単にコピーを重ね合わせる写像、iX : 0 → X は空集合の埋め込みです。このモノイドによるモノイダルスタンピングモナドを作り、そのクライスリ圏が例外付き計算の圏です。
今回は、例外変換φを付けるので、わずかに異なった構成となります。f: A → B +: X と φ : X → Y を組み合わせた (f, :φ): A → B +: Y のような計算を射とする圏を考えたいのです。(f, :φ): A → B +: Y と (g, :ψ): B → C +: Z の直列結合は次のように定義すればいいでしょう。
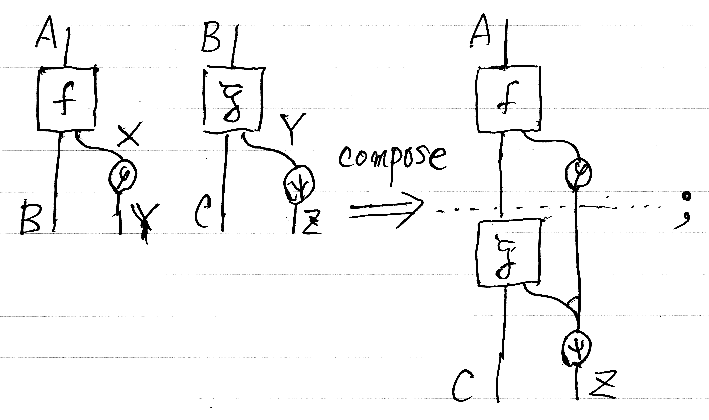
例外ワイヤーの合流しているところは、∇Y: Y + Y → Y を使っています。
これでも計算に不自由はしませんが、射の域と余域がいまいちハッキリしません。そこで、(f, :φ): A +: X → B +: Y と (g, :ψ): B +: Y → C +: Z となるように一工夫します。例外型を入力の一部と考えます。次の図を見れば何をしているか分かるでしょう。
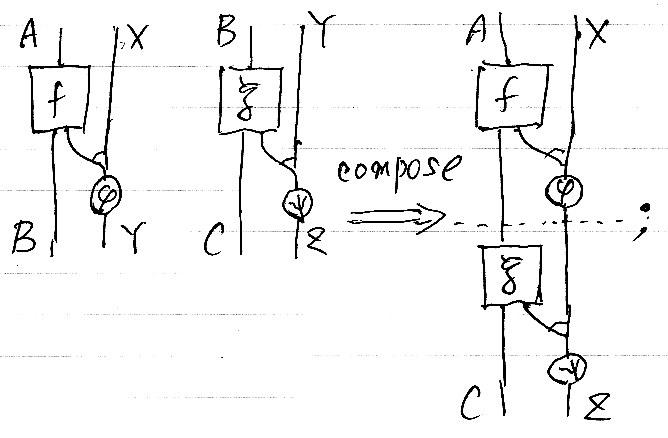
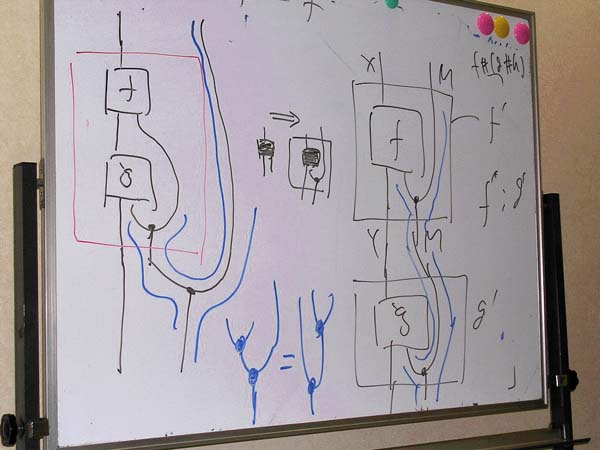
この方式だと、直列結合が素直にできます。次のホワイトボードは、だいぶ前(2009年)に口頭でほぼ同じことを説明したときのもの。
例外付き計算のインデックス付き圏/グロタンディーク構成
(f, :φ): A +: X → B +: Y のような形の計算を射とする圏を絵算をベースにして手作りすることができます。が、別な定式化をした上で大道具を使っても構成できます。
純粋計算の圏Cと例外の圏Eは与えられているとします。Eの対象(つまり例外型)Xを固定して、f:A → B +: X のような形の射を考えます。このような射達は圏を構成しますが、最初に選んだXに依存するので D[X] と書くことにします。圏D[X]をもう少し詳しく言うと:
- 圏D[X]の対象は、圏Cの対象と同じである; |D[X]| = |C|
- 圏D[X]のホムセットD[X](A, B)は、A → B +: X という形の射からなる。
- A → B +: X と B → C +: Y の結合は、クライスリ結合を使う。
- A → A +: X という恒等射は、クライスリ恒等射を使う。
要するに、A |→ A + X という直和スタンピングモナドのクライスリ圏がD[X]となります。
今述べた手順で、Eの対象Xごとに、圏D[X]を対応付けることができました。φ:X→Y in E があるとき、共変関手 φ*:D[X]→D[Y] は、例外変換φの後結合(post compose)で定義できます。D[-] と (-)* の全体を改めてDと書くと、Dは、圏Eから圏の圏Catへの関手となっています。つまり、インデックス付き圏(indexed category)です。インデックス付き圏の定義は反変関手なので、これは余インデックス付き圏ですが、矢印の向きが逆転するだけで同じことです。
インデックス付き圏(または余インデックス付き圏)があると、それからグロタンディーク構成(Grothendieck construction)または平坦化(flattening)と呼ばれる方法でファイバー圏を作れます。その作り方は「インデックス付き圏のグロタンディーク構成」に書いておきました。そこで使った絵を再掲しておくと:
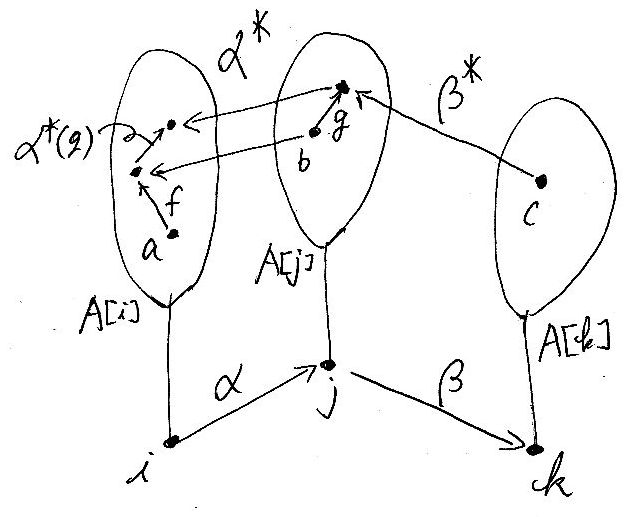
地面から木がたくさん生えた森のようなところでゴニョゴニョします。ゴニョゴニョの結果できあがった圏(ファイバー構造の全体圏)が、絵算で手作りした圏と同じ(圏同型な)圏となります。
と、そんな感じで、例外付き計算は不純計算のなかでも扱いやすくキレイな構造を持っています。比喩的に言えば「不純物も析出して結晶を見ると美しい」ってことかな。
例外の話は次の記事でもしています。
*1:後で触れるように、実際は余インデックス付き圏です。