ツリー書き換え系とマックレーンの一貫性定理 - 檜山正幸のキマイラ飼育記 (はてなBlog)

モノイド圏に対するマックレーンの一貫性定理（Mac Lane's coherence theorem for monoidal categories）は有名なんですが、それが主張する内容を把握しづらい定理です。同値な内容を様々な形で述べることができます。ここでは、ツリー書き換え系との関係でマックレーンの一貫性定理を定式化してみます -- この形でも謎な感じは払拭できないのですが、応用には便利な形になります。

なお、この記事は、「自然演繹の再構築への道」で述べた計画の一部です。

内容：

マックレーンの一貫性定理
定式化の概要
二分木
二分木の基本変形
二分木のパスと部分ツリー
ツリーの単純書き換え
ツリー書き換えの圏
評価関手
単純ツリー書き換えの評価
ツリー書き換えによるマックレーンの一貫性定理の記述

マックレーンの一貫性定理

マックレーンの一貫性定理については、nLabのエントリーがあります。

coherence theorem for monoidal categories

このnLabエントリーには、6種類の形で定理が述べられています。証明は別なエントリーにあります（2016年7月時点では一部未完）

Mac Lane's proof of the coherence theorem for monoidal categories

ここでは、MITのテンソル圏のコースの講義資料にある次の形を採用します。

Let X₁, ..., X_n ∈ C. Let P₁, P₂ be any two parenthesized products of X₁, ..., X_n (in this order) with arbitrary insertions of unit objects 1.
Let f, g : P₁ → P₂ be two isomorphisms, obtained by composing associativity and unit isomorphisms and their inverses possibly tensored with identity morphisms.
Then f = g.
X₁, ..., X_n をモノイド圏Cの対象とする。P₁, P₂ は、X₁, ..., X_n 達を掛け算（モノイド積）して得られる対象とする。掛け算は括弧により優先順位が曖昧性なく指定されていて、X₁, ..., X_n がこの順で出現しなくてはならない。また、モノイド単位1が因子として適当に挿入されることを許すとする。
f, g : P₁ → P₂ は2つの同型射とする。これらの同型射は、結合律子、左単位律子、右単位律子、それらの逆、恒等射を、射の結合とモノイド積で組み合わせたものとする。
上記の設定で、f = g が成立する。

元の講義資料では、一貫性定理を、「任意のモノイド圏には厳密化（strictification）が存在する」ことを仮定して証明しています。厳密化は、ひとつ前の講義資料において、モノイド圏Cの自己関手圏End(C)への巧みな“表現”を構成することで示しています。

厳密化に関する別な議論として：

Title: Turning Monoidal Categories into Strict Ones
Author: Peter Schauenburg
URL: http://nyjm.albany.edu/j/2001/7-16.pdf

ブレイド付きモノイド圏の場合の概要は：

Title: MacLane's coherence theorem expressed as a word problem
Author: Paul-Andre Mellies
URL: https://hal.archives-ouvertes.fr/hal-00154213/document

定式化の概要

ここでやることは、マックレーンの一貫性定理の表現方法を多少変えるだけです。Cが与えられたモノイド圏として、別な圏Bと、Bからの関手 F:B→C を構成します。関手Fの像として得られる部分圏 B'⊆C がやせた圏である、という主張がマックレーンの一貫性定理となります。

圏Bは、完全に組み合わ的／帰納的に構成します。圏Bの対象は、二分木です。そして、圏Bの射は、ツリー（二分木）の書き換え（rewriting）です。関手Fは、ツリーを式とみなしての評価写像（evaluator）になります。

このような形にすると、「式に、その計算結果である値を対応させる」という、プログラミング言語ではお馴染みの意味論になります。見慣れた形ならば、幾分かは分かりやすく親しみやすいのではないか、と思うわけです。

二分木

Wを集合として、i∈W が特定されているとします。iを含むのでWは空ではありません。W = {i} が最小のケースです。Wの要素をリーフ（葉、末端）とする二分木（binary tree）は、次のように帰納的に定義されます。

Wの要素は二分木である。
s, tが二分木ならば、(s∧t) は二分木である。
以上により定義されるものだけが二分木である。

Wから作られた二分木全体の集合を BinTree(W) とします。

W = {i, a, b} のとき、(a∧((a∧b)∧i)) は二分木（BinTree(W)の要素）の例です。∧は、ここでは論理ANDではなくて、下の図のようなツリーの形状に似せた記号です。双子サクランボの枝の形ですね。

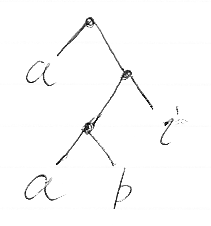
リーフノードはWの要素ですが、「ノードのラベルとしてWの要素を使っている」とみなしてもかまいません。Wをラベル集合と解釈するなら：

リーフノードは、Wの要素でラベル付けされている。
リーフではないノードにはラベルが付いてない。
ラベルが付いたリーフノードが1個だけでも（特殊な）ツリーとみなす。

リーフでないノードをブランチノードと呼ぶことにします。

ツリー（二分木）を図示する場合は、リーフノードはWの要素として書き、ブランチノードは無名のドットで表します。ブランチノードは、必ず左の子ツリーと右の子ツリーを持ちます。

二分木の基本変形

s, t, p, q, r などはBinTree(W)の要素、つまり二分木を表すとします。ある形状の二分木が与えられたとき、それを別な二分木に変形する操作を考えます。その変形操作を列挙しましょう。

左スイッチ： ((p∧q)∧r) → (p∧(q∧r))
右スイッチ： (p∧(q∧r)) → ((p∧q)∧r)
iの左削除： (i∧p) → p
iの左挿入： p → (i∧p)
iの右削除： (p∧i) → p
iの右挿入： p → (p∧i)

左スイッチは「左のブランチノードを右へスイッチする」の意味です。6つの操作に略称を付けておきます。

名前	略称	適用可能なツリー
左スイッチ	LSw	((p∧q)∧r) の形のツリー
右スイッチ	RSw	(p∧(q∧r)) の形のツリー
iの左挿入	LIns	任意のツリー
iの左削除	LDel	(i∧p) の形のツリー
iの右挿入	RIns	任意のツリー
iの右削除	RDel	(p∧i) の形のツリー

これら6つの操作をツリー（二分木）の基本変形と呼びましょう。LSw←→RSw、LIns←→LDel、RIns←→RDe は互いに逆になっています。これを考慮して基本変形を絵に描くと、次のようです。

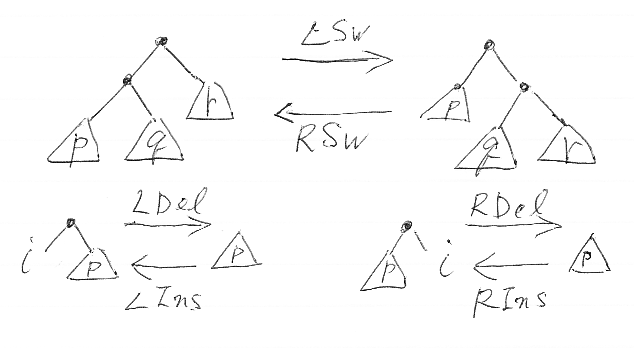
基本変形をBinTree(W)からBinTree(W)への部分写像と考えて、すぐ上で約束した略称を写像の名前として使います。例えば、LSwは BinTree(W)→BinTree(W) という部分写像です。部分写像はまた、BinTree(W)→(BinTree(W) + {⊥}) という写像と考えることもできます。ここで、⊥は未定義を意味する特殊な値です。

これらの基本変形は、結合律子（associator）、左単位律子（left unitor）、左単位律子（right unitor）を組み合わせ的に表現したものです（律子（りつし）に関しては「律子からカタストロフへ」を参照してください）。

二分木のパスと部分ツリー

二分木内のノードを正確に指し示すために、ツリーのパスを考えましょう。パスは、{1, 2}^*の要素だとします。{1, 2}^*の要素は、数字1か2を並べた列ですが、コンピューター屋さんの風習に従って、あいだにスラッシュ（/）をはさみます。また、先頭にもスラッシュを付けることにします。すると、空列は /、121は /1/2/1 となります。1が左、2が右を表すと約束します。

BinTree(W)の要素である二分木tを、Wをラベル集合とするラベル付きツリーと考えて、パスξの位置のノードラベルを label(t, ξ) と書きます。labelは、BinTree(W)×{1, 2}^*→(W + {⊥}) という写像になります。

t = (a∧((a∧b)∧i)) のとき、

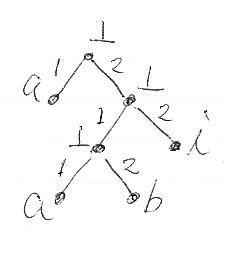
label(t, /) = ⊥
label(t, /1) = a
label(t, /2) = ⊥
label(t, /2/1) = ⊥
label(t, /2/2) = i
label(t, /2/2/1) = ⊥
label(t, /2/1/1) = a
label(t, /2/1/2) = b

ツリーの特定のノードを指定すると、そのノードと子孫達からなるサブツリーが決まります。これを、subtree(t, ξ) と書くことにします。
subtreeは、BinTree(W)×{1, 2}^*→(BinTree(W) + {⊥}) という写像になります。

先と同じく t = (a∧((a∧b)∧i)) なら、

subtree(t, /) = (a∧((a∧b)∧i))
subtree(t, /1) = a
subtree(t, /2) = ((a∧b)∧i)
subtree(t, /2/1) = (a∧b)
subtree(t, /2/2) = i
subtree(t, /2/2/1) = ⊥
subtree(t, /2/1/1) = a
subtree(t, /2/1/2) = b

ツリーの単純書き換え

与えられたツリーを別なツリーに書き換えるステップを単純書き換え（simple rewrite/rewriting）と呼びましょう。以下に正確な定義を書いていきます。

単純書き換えは次のもので構成されます。

二分木t （t∈BinTree(W)）
パスξ （ξ∈{1, 2}^*）
基本変形u （u∈{LSw, RSw, LIns, RIns, LDel, RDel}）

これらは次の条件を満たすとします。

subtree(t, ξ) が定義されている（つまり、subtree(t, ξ) ≠ ⊥）。
subtree(t, ξ) にuを適用可能である。

この条件が成立しているなら、u(subtree(t, ξ)) が定義できます。例えば、

t = (a∧((a∧b)∧i))
ξ = /2
u = RDel

のとき、

subtree(t, ξ) = subtree(t, /2) = ((a∧b)∧i)

となり、これにRDelを適用可能であり、

u(subtree(t, ξ)) = RDel(subtree(t, /2)) = RDel(((a∧b)∧i)) = (a∧b)

です。

tにおけるsubtree(t, ξ)を、u(subtree(t, ξ))で置き換えた結果を subst(t, ξ, u) とします。例えば、

subst((a∧((a∧b)∧i)), /2, RDel) = (a∧(a∧b))

となります。

ツリーtの単純書き換えは、t, ξ, u で決まりますが、書き換え（部分ツリーの置換）の結果である t' = subst(t, ξ, u) も一緒にして、[t, (ξ, u), t'] の形にします。この記法の意味は次のとおりです。

ツリーtにおいて、パスξで指定されるサブツリーを基本変形uにより書き換えた結果はt'である。

ツリー書き換えの圏

ツリーtの単純書き換えを [t, (ξ, u), t'] の形で表しましたが、これを一般化して次の形式を考えます。

[t₀, (ξ₀, u₀), t₁, ..., t_n-1, (ξ_n-1, u_n-1), t_n]

ここで、0≦i＜n に対して [t_i, (ξ_i, u_i), t_i+1] は単純書き換えになっているとします。

この形のリストは、長さが 3, 5, 7, ... と奇数になりますが、ツリーtだけを含む長さ1のリスト [t] も一緒に考えることにします。

今説明した形のリストをツリーの書き換え（rewrite, rewriting）と呼びます。ツリーの書き換えは、ツリーの単純書き換えの列です。ツリーの書き換えを表すリストは長さが 2n + 1 です。n = 0 のときは [t] の形、n ＞ 0 なら、[t₀, (ξ₀, u₀), t₁, ..., t_n-1, (ξ_n-1, u_n-1), t_n] の形をしています。nを、書き換えのステップ数（number of steps）と呼ぶことにします。nステップ（n ＞ 0）の書き換えを [t₀, ..., t_n] のように略記していいとします。

さて、ツリーの書き換えを射とする圏を作りたいのですが、しりとりの圏と大差ないのでサッサと進めます。

Wは特定元iが指定された集合として、圏BTR_Wを次のように定義します。

対象の集合は、Obj(BTR_W) = |BTR_W| = BinTree(W) とする。
射の集合は、Mor(BTR_W) = (BinTree(W) に属するツリーを書き換える書き換え全体の集合)とする。
域は、dom([t]) = t、dom([t₀, ..., t_n]) = t₀ と定義する。
余域は、cod([t]) = t、cod([t₀, ..., t_n]) = t_n と定義する。
結合は、しりとり結合と同じ。
恒等射は、id_t = [t]

これらのデータから実際に圏が出来るのを確認するのは容易です。

圏BTR_Wの射は、ステップ数がn（n≧0）のツリー書き換えすが、それはn個の単純ツリー書き換えの結合として一意に表すことができます。つまり、射の結合演算子を「;」として、次の等式が成立します。

[t₀, (ξ₀, u₀), t₁, ..., t_n-1, (ξ_n-1, u_n-1), t_n] = [t₀, (ξ₀, u₀), t₁];...;[t_n-1, (ξ_n-1, u_n-1), t_n]

評価関手

次に、圏BTR_Wからモノイド圏 C = (C, $\otimes$ , I) への関手を構成します。ただし、ψ:W→|C| は与えられているとして、ψ(i) = I の条件を付けます。

ψから決まる関手 F_ψ:BTR_W→C とします。記号の乱用で、F = F_ψ とも書きます。

関手Fの対象部分（object part）は、次のように再帰的に定義します。

a∈W のとき、F(a) := ψ(a)。特に、F(i) := ψ(i) = I
F((s∧t)) := F(s) $\otimes$ F(t)

次に、Fの射部分（morphism part）を定義するのですが、単純書き換え [t, (ξ, u), t'] に対する F([t, (ξ, u), t']) は定義されていると仮定します。次の節で実際の定義をします。

F([t, (ξ, u), t']) が定義されているなら、前節の最後で述べた等式を意識して：

F([t₀, (ξ₀, u₀), t₁, ..., t_n-1, (ξ_n-1, u_n-1), t_n]) := F([t₀, (ξ₀, u₀), t₁]);...;F([t_n-1, (ξ_n-1, u_n-1), t_n])

ここで、右辺の「;」は圏Cにおける射の結合です。また、

F([t]) = id_F(t)

以上のデータから定義される F = F_ψ が関手になることも容易に確認できます。

この関手 F = F_ψ:BTR_W→C を、圏Cを値とする評価関手（evaluation functor）と呼ぶことにします。

単純ツリー書き換えの評価

前節で先延ばしにした F([t, (ξ, u), t']) の定義を述べます。以下で、α, λ, ρ はモノイド圏Cの結合律子、左単位律子、右単位律子とします。

まず ξ = / （ルート）の場合を定義します。

u = LSw、t = ((p∧q)∧r) のとき、F([t, (/, u), t']) = α_{F(p),F(q),F(r)}
u = RSw、t = (p∧(q∧r)) のとき、F([t, (/, u), t']) = α_{F(p),F(q),F(r)}^-1
u = LIns のとき、F([t, (/, u), t']) = λ_F(t)^-1
u = LDel、t = (i∧p) のとき、F([t, (/, u), t']) = λ_F(p)
u = RIns のとき、F([t, (/, u), t']) = ρ_F(t)^-1
u = RDel、t = (p∧i) のとき、F([t, (/, u), t']) = ρ_F(t)

ξ ≠ / のとき、p = subtree(t, ξ) とします。サブツリーp上では、F([p, (/, u), p']) が定義できます。サブツリーp上の定義を、二分木全体tまで拡張すればいいのですが、それには、「左子ツリーから親ツリー」「右子ツリーから親ツリー」への拡張を定義すれば十分です。その拡張を繰り返し適用すればいいからです。