二分木の平坦化定理

圏論の計算をしていて、組み合わせ的な議論に行き着くことはよくあります。モノイド圏をいじっていたら、二分木のプリミティブな組み合わせ的事実が必要になりました。その話をします。 $\newcommand{\I}{\mathrm{I}} \newcommand{\A}{\wedge } \newcommand{\L}{\mathrm{L} } \newcommand{\moveTo}{\rightsquigarrow } \newcommand{\cat}[1]{\mathcal{#1} }$

内容：

二分木とリスト
リストのスプライシングと平坦化
二分木の平坦化定理
何に使うか？

二分木とリスト

二分木〈binary tree〉のテキスト記法としては、「BUNツリーの亜群オペラッド構造 // BUNツリー」で導入した記法を使います。単に「BUNツリー」と言った場合でも、「BUNツリーの亜群オペラッド構造 // 伸縮同値関係」で導入した伸縮同値関係の同値類を意味します。それ以前の記事「反ラックス・モノイド関手の一般余結合律」で定義した二分木は、BUNツリー（の伸縮同値類）と考えることができます。

幅（プレースホルダーの個数）が $n$ であるBUNツリーの集合は、 $|{\bf BUNTree}(n)|$ と書きます。絶対値記号で囲っているのは、 ${\bf BUNTree}(n)$ と書くと単なるBUNツリーだけではなくて、マックレーン変形などの高次構成素も持つ複雑な構造を表すからです。

$n = 0, 1, 2, \cdots$ に対して、BUNツリー $\L(n)$ を定義します*1。

$\L(0) = \,!$
$\L(1) = (\I-)$
$\L(2) = (-\A-)$
$\L(3) = ( (-\A-)\A-) = (\L(2)\A-)$
$\L(4) = ( ( (-\A-)\A-)\A-) = (\L(3)\A-)$
$\L(k + 1) = (\L(k)\A-)$

$L(0), L(1)$ はほんとの二分木ではありませんが、“用語の乱用”で二分木と呼んでしまいます。プレースホルダー “ $-$ ” の出現に左から順に番号を付けて、二分木を次のように（ブラケット囲みの）リストと同一視します。

$\L(0) = \,! = []$
$\L(1) = (\I 1) = [1]$
$\L(2) = (1\A 2) = [1, 2]$
$\L(3) = ( (1\A 2)\A 3) = (\L(2)\A 3) = [1, 2, 3]$
$\L(4) = ( ( (1\A 2)\A 3)\A 4) = (\L(3)\A-) = [1, 2, 3, 4]$
$\L(k + 1) = (\L(k)\A k+1) = [1, \cdots, k, k + 1]$

リストの囲み記号をブラケットにしているのは、ツリーの囲み記号の丸括弧と区別するためで他意はありません。

リストのスプライシングと平坦化

二分木（用語の乱用） $\L(n)$ に関して、BUNツリーとしての幅（プレースホルダーの個数）とリストとしての長さは同じです。

$\quad \mathrm{width}(\L(n)) = \mathrm{length}(\L(n)) = n$

あるいは、 $\L(n) \in |{\bf BUNTree}(n)|$ 。

$1 \le i \le n$ として、 $\L(n)$ の $i$ 番目の位置に $\L(m)$ を置換スプライシングすると次のようになります。

$\quad [1, \cdots, i-1, [1, \cdots, m], i+1, \cdots,n ]$

何をやったのかと言うと：

$\L(n)$ の $i$ 番目の要素（番号付きプレースホルダー）を取り除き、“穴”を開ける。
その穴に、 $\L(n)$ を挿入する。

これだと、プレースホルダーの番号が左から右に増えてません。それを調整すると：

$\quad [1, \cdots, i-1, [i, \cdots, m + i - 1 ], m + i, \cdots, m + n -1]$

入れ子のリストを平坦にすると：

$\quad [1, \cdots, i-1, i, \cdots ,m + i - 1 , m + i, \cdots, m + n -1]$

以上の変形プロセスを、二分木（BUNツリー）へのマックレーン変形で実行できます。このことを示しましょう。

ここから先、絵で説明しています。視覚的直感に頼っているので厳密性に欠けますが、それでも説得力は十分にあると思います。

置換スプライシングの一般的な状況は次のように描けます。

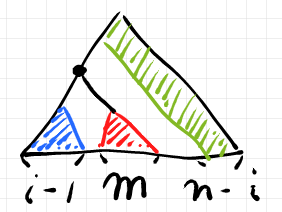
赤い部分が挿入された $\L(m)$ で、 $\L(n)$ は2つの部分（青と緑）に分断されます。リスト形式で書くなら次のようです。

$\quad [1, \cdots, i-1, [i, \cdots, m + i - 1 ], m + i, \cdots, m + n -1]$

入れ子を平坦化するプロセスが、マックレーン変形で実行できることを、自然数 $m$ に関する数学的帰納法で示します。 $m = 0, 1$ の場合は個別に調べます。

まず、 $m = 0$ の場合。

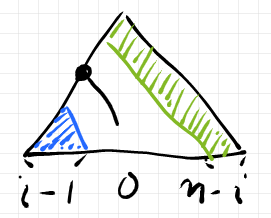
この場合は、黒丸を相対ルートとするサブツリーにマックレーン基本変形 $\mathrm{RDel}$ を適用すれば平坦化できます。リスト形式で書くなら次のようです。

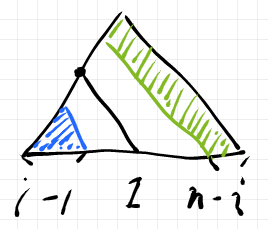
$\quad [1, \cdots, i-1, [ ], i, \cdots, n -1] \\ \moveTo [1, \cdots, i-1, i, \cdots, n -1]$

次に、 $m = 1$ の場合。

この場合は、何もすることがありません。リスト形式で書くなら次のようです。

$\quad [1, \cdots, i-1, [i ], 1 + i, \cdots, 1 + n -1]\\ \moveTo [1, \cdots, i-1, i, 1 + i, \cdots, 1 + n -1]$

数学的帰納法のステップとして、 $\L(m)$ の置換スプライシングの平坦化は出来るとして、 $\L(m+1)$ の場合を考えましょう。

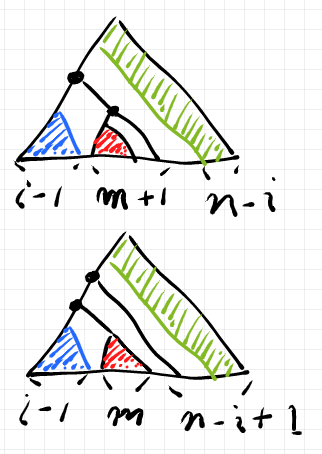
黒丸を相対ルートとするサブツリーにマックレーン基本変形 $\mathrm{RSw} = \mathrm{LSw}^{-1}$ を適用すると、 $\L(m)$ を置換スプライシングした形に変形できます。数学的帰納法の仮定から、この形はマックレーン変形で平坦化できるので、全体もマックレーン変形で平坦化できます。

何に使うか？

「余計な話？厳密2-亜群オペラッドとモノイド圏」で、 $\mathrm{S2GO}(\cat{K})$ のオペラッド結合を定義する際に、対象のリストの置換スプライシング $\vec{A} *_i \vec{B}$ を使っています。この演算 $*_i$ （記号はオペラッド結合とオーバーロードしている）をちゃんと定義するには、二分木の平坦化定理が必要です。